从一点一滴开始学习了解LDA-Learning Linear Discriminate Analysis from scratch
从一点一滴开始学习了解LDA-Learning Linear Discriminate Analysis from scratch
- 前言
- 参考文献
- 初涉LDA
- 看代码
- 看概念
- 看例子
- 类均值
- 类协方差矩阵
- 类内散度矩阵
- 类间散度矩阵
- 求解特征值和特征向量
- 多分类LDA的推导
- 类内散度矩阵
- 类间散度矩阵
- 投影空间
- 类内均值和空间均值
- 散度矩阵
- 后记
- 附录
前言
learning ** from scratch大都翻译为从0开始学叉叉,不过真没见过谁能从0开始学一个比较深的技术或者理论,所以这篇名戏谑一下这个词。接触LDA刚开始就对Discraminiate翻译记不住,是差异、辨别,歧视,为什么选择判别作为汉语呢?这只是一系列疑问的开始,因为刚开始接触这个概念,确实连一知半解都谈不上,只是从别人画的图中大概明白是干啥的,那么这个技术能帮助我解决现在的研究课题吗?下面总结记述对这个术语背后理论和实践的学习。正文将参考文献放在第一部分,因为没有这些文献真的无法理解和使用这项技术。而本文很多代码和样例都来自这些文献,先感谢各位作者的知识分享。
参考文献
- 《机器学习》 周志华 著 清华大学出版社.
- A Tutorial on Data Reduction-Linear Discriminant Analysis, Shireen Elhabian and Aly A. Farag, University of Louisville, CVIP Lab
- Linear Discriminant Analysis (LDA) https://www.python-course.eu/linear_discriminant_analysis.php
- Wine Data Set https://archive.ics.uci.edu/ml/datasets/wine
- Linear Discriminant Analysis In Python. Cory Maklin. https://towardsdatascience.com/linear-discriminant-analysis-in-python-76b8b17817c2
初涉LDA
各种介绍此算法的文章都喜欢用一个二维分类点图,加两条直线为读者展现算法的魅力,这样做就是将二维数据最终投影到一维直线上,变成一维数据的同时,令分类的点更加直观,从而引出LDA的初衷:同类投影点尽可能接近,异类投影点尽可能远离。
看代码
一个欧洲域名的网站Python Machine Learning Tutorial对LDA应用很简单明了的演示了一下,在原文的基础上,我增加了测试集的操作,使得结果更加一目了然:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib import style
from sklearn.model_selection import train_test_split
style.use('fivethirtyeight')
from sklearn.neighbors import KNeighborsClassifier
# 0. Load in the data and split the descriptive and the target feature
df = pd.read_csv('data/wine.data', sep=',',
names=['target', 'Alcohol', 'Malic_acid', 'Ash', 'Akcakinity', 'Magnesium', 'Total_pheonols',
'Flavanoids', 'Nonflavanoids', 'Proanthocyanins', 'Color_intensity', 'Hue', 'OD280', 'Proline'])
X = df.iloc[:, 1:].copy()
target = df['target'].copy()
X_train, X_test, y_train, y_test = train_test_split(X, target, test_size=0.3, random_state=0)
# 1. Standardize the data
for col in X_train.columns:
X_train[col] = StandardScaler().fit_transform(X_train[col].values.reshape(-1, 1))
# 1. Standardize the data
for col in X_test.columns:
X_test[col] = StandardScaler().fit_transform(X_test[col].values.reshape(-1, 1))
# 2. Compute the mean vector mu and the mean vector per class mu_k
mu = np.mean(X_train, axis=0).values.reshape(13,
1) # Mean vector mu --> Since the data has been standardized, the data means are zero
mu_k = []
for i, orchid in enumerate(np.unique(df['target'])):
mu_k.append(np.mean(X_train.where(df['target'] == orchid), axis=0))
mu_k = np.array(mu_k).T
# 3. Compute the Scatter within and Scatter between matrices
data_SW = []
Nc = []
for i, orchid in enumerate(np.unique(df['target'])):
a = np.array(X_train.where(df['target'] == orchid).dropna().values - mu_k[:, i].reshape(1, 13))
data_SW.append(np.dot(a.T, a))
Nc.append(np.sum(df['target'] == orchid))
SW = np.sum(data_SW, axis=0)
SB = np.dot(Nc * np.array(mu_k - mu), np.array(mu_k - mu).T)
# 4. Compute the Eigenvalues and Eigenvectors of SW^-1 SB
eigval, eigvec = np.linalg.eig(np.dot(np.linalg.inv(SW), SB))
# 5. Select the two largest eigenvalues
eigen_pairs = [[np.abs(eigval[i]), eigvec[:, i]] for i in range(len(eigval))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real)) # Select two largest
# 6. Transform the data with Y=X*w
Y = X_train.dot(w)
Y_p = X_test.dot(w)
# Plot the data
fig = plt.figure(figsize=(10, 10))
ax0 = fig.add_subplot(111)
ax0.set_xlim(-3, 3)
ax0.set_ylim(-4, 3)
for l, c, m in zip(np.unique(y_train), ['r', 'g', 'b'], ['s', 'x', 'o']):
ax0.scatter(Y[0][y_train == l],
Y[1][y_train == l],
c=c, marker=m, label=l, edgecolors='black')
ax0.legend(loc='upper right')
for l, c, m in zip(np.unique(y_test), ['c', 'k', 'm'], ['p', '*', 'h']):
ax0.scatter(Y_p[0][y_test == l],
Y_p[1][y_test == l],
c=c, marker=m, label=l, edgecolors='red')
ax0.legend(loc='upper right')
# Plot the voroni spaces
means = []
for m, target in zip(['s', 'x', 'o'], np.unique(y_train)):
means.append(np.mean(Y[y_train == target], axis=0))
ax0.scatter(np.mean(Y[y_train == target], axis=0)[0], np.mean(Y[y_train == target], axis=0)[1], marker=m, c='black',
s=100)
mesh_x, mesh_y = np.meshgrid(np.linspace(-3, 3), np.linspace(-4, 3))
mesh = []
for i in range(len(mesh_x)):
for j in range(len(mesh_x[0])):
date = [mesh_x[i][j], mesh_y[i][j]]
mesh.append((mesh_x[i][j], mesh_y[i][j]))
NN = KNeighborsClassifier(n_neighbors=1)
NN.fit(means, ['r', 'g', 'b'])
predictions = NN.predict(np.array(mesh))
ax0.scatter(np.array(mesh)[:, 0], np.array(mesh)[:, 1], color=predictions, alpha=0.3)
plt.show()
这段代码运行完的会画出如下的点图,其中图例的第一个123表示训练集的点阵,第二个123表示测试集的点阵。
 上述图形说明了哪些问题呢?要想看清楚发生了什么,还要从原始数据入手,这个数据来自于UCI Marchine Learning Repository: Wine Data Set,记录了来自三个产区的不同葡萄酒的几十种化学成分,数据内容是这样的:
上述图形说明了哪些问题呢?要想看清楚发生了什么,还要从原始数据入手,这个数据来自于UCI Marchine Learning Repository: Wine Data Set,记录了来自三个产区的不同葡萄酒的几十种化学成分,数据内容是这样的:
| Region | Alcohol | Ash | Alcalinity of ash | Magnesium | Total phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color intensity | Hue | OD280/OD315 of diluted wines | Proline |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.8 | 3.06 | .28 | 2.29 | 5.64 | 1.04 | 3.92 |
Region是我们要的目标类别1,2,3。那么如何通过LDA挖掘13维数据,寻找这种映射呢?上面的代码实现这个功能,并且将13维的数据降到2维,画在了图上,让读者一目了然。通过上图可以看出,用训练集和拟合出来的 w w w,可以很好的将测试集的数据完成降维和分类。
看概念
对于二维数据集,就是寻找一条直线,令数据投影到这条直线上,并且满足同类投影点尽可能接近,异类投影点尽可能远离;新样本按照同样的方法投影到这条直线上,根据投影点的位置就可以确定样本的类别。类推到多维空间。概念非常朴素却蕴藏精辟的论点,投射、直线。或者说,如何找到这样一条“直线”已经让我这个半路出家的炼丹师差不多快晕死了。据说这是矩阵空间里的重要知识,我也许当初在大学里学过,只是很快的还给老师了。先囫囵吞枣的记住这个概念吧。下面引用(重抄一遍)西瓜书里的原文标准定义:
【1】给定数据集 D = ( x i , y i ) ∑ 1 n , y i ∈ 0 , 1 D={(x_i , y_i)}\sum_1^n,\quad y_i \in{0, 1} D=(xi,yi)∑1n,yi∈0,1, 令 X i 、 μ i 、 ∑ i X_i 、 \mu_i、\sum_i Xi、μi、∑i 分别表 示 第 i ∈ i\in i∈ {0 , 1} 类示例的集合、均值向量、协方差矩阵。若将数据投影到直线 w w w上 ,则两类样本的中心在直线上 的投影分别为 w T μ 0 w^T\mu_0 wTμ0 和 w T μ 1 w^T\mu_1 wTμ1;若将所有样本点都投 影到直线上,则两类样本的 协方差分别为 w T ∑ 0 w w^T\sum_0 w wT∑0w 和 w T ∑ 1 w w^T\sum_1 w wT∑1w. 由于直线是一维空间,因此 w T μ 0 w^T\mu_0 wTμ0 、 w T μ 1 w^T\mu_1 wTμ1、 w T ∑ 0 w w^T\sum_0 w wT∑0w 和 w T ∑ 1 w w^T\sum_1 w wT∑1w均为实数.
此处协方差矩阵是何物?
样本中心投影为啥是这个?
多维空间就不是实数了?
很多基础概念不甚了了。
欲使同类样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即 w T ∑ 0 w w^T\sum_0 w wT∑0w + w T ∑ 1 w w^T\sum_1 w wT∑1w 尽可能小;而欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大,即 ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 ||w^T\mu_0 - w^T\mu_1||_2^2 ∣∣wTμ0−wTμ1∣∣22 尽可能大.同时考虑二者,则可得到欲最大化的目标:
J ( w ) = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T ∑ 0 w + w T ∑ 1 w = w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) w w T ( ∑ 0 + ∑ 1 ) w = w T S b w w T S w w \begin{aligned} J(w)&=\frac {||w^T\mu_0 - w^T\mu_1||_2^2}{w^T\sum_0 w + w^T\sum_1 w} \\ &= \frac {w^T(\mu_0 - \mu_1)(\mu_0 - \mu_1) w}{w^T(\sum_0 + \sum_1) w}\\ &=\frac {w^T\bold S_b w}{w^T\bold S_w w} \end{aligned} J(w)=wT∑0w+wT∑1w∣∣wTμ0−wTμ1∣∣22=wT(∑0+∑1)wwT(μ0−μ1)(μ0−μ1)w=wTSwwwTSbw
此处定义了类内散度矩阵(within-class scatter matrix):
S w = ∑ 0 + ∑ 1 = ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 1 ) ( x − μ 1 ) T \begin{aligned} \bold{S_w} &= \sum_0+\sum_1\\ &= \sum _{x\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum _{x\in X_1}(x-\mu_1)(x-\mu_1)^T \end{aligned} Sw=0∑+1∑=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T
和类间散度矩阵(between-class scatter matrix):
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T \bold S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T Sb=(μ0−μ1)(μ0−μ1)T
以上定义出了LDA的最大化目标(广义瑞利商)(晕*3)。那么如何根据最大化目标来求得我们心心念的 w w w呢?《西瓜书》已经用完全看不懂了。但这很自然的想到了典型的优化方法,求导并令导数等于0,参考文献【2】给出了公式推导:
d d w J ( w ) = d d w ( w T S b w w T S w w ) = 0 ⇒ ( w T S w w ) d d w ( w T S b w ) − ( w T S b w ) d d w ( w T S w w ) = 0 ⇒ ( w T S w w ) 2 S b w − − ( w T S b w ) 2 S w w = 0 \begin{aligned} \frac{d}{dw}J(w) &= \frac{d}{dw} \left(\frac{w^T\bold S_b w}{w^T\bold S_w w} \right)=0\\ &\Rightarrow (w^T\bold S_w w) \frac{d}{dw} \left({w^T\bold S_b w} \right)-(w^T\bold S_b w) \frac{d}{dw} \left({w^T\bold S_w w} \right)=0\\ &\Rightarrow (w^T\bold S_w w)2S_bw - -(w^T\bold S_b w) 2S_ww=0 \end{aligned} dwdJ(w)=dwd(wTSwwwTSbw)=0⇒(wTSww)dwd(wTSbw)−(wTSbw)dwd(wTSww)=0⇒(wTSww)2Sbw−−(wTSbw)2Sww=0
令等式除以 w T S w w w^T\bold S_w w wTSww:
⇒ ( w T S w w w T S w w ) S b w − ( w T S b w w T S w w ) = S w w = 0 ⇒ S b w − J ( w ) S w w = 0 ⇒ S w − 1 S b w − J ( w ) w = 0 \begin{aligned} &\Rightarrow \left(\frac{w^T\bold S_w w}{w^T\bold S_w w} \right)S_bw - \left(\frac{w^T\bold S_b w}{w^T\bold S_w w} \right)=S_ww=0\\ &\Rightarrow S_bw -J(w)S_ww=0\\ &\Rightarrow S_w^{-1}S_bw -J(w)w=0\\ \end{aligned} ⇒(wTSwwwTSww)Sbw−(wTSwwwTSbw)=Sww=0⇒Sbw−J(w)Sww=0⇒Sw−1Sbw−J(w)w=0
上式就变成了矩阵求特征值的问题,公式如下 :
⇒ S w − 1 S b w = λ w λ = J ( w ) \begin{aligned} \Rightarrow & S_w^{-1}S_bw =\lambda w\\ &\lambda = J(w) \end{aligned} ⇒Sw−1Sbw=λwλ=J(w)
这个 λ \lambda λ被西瓜书引用为拉格朗日乘子,该公式可以理解为针对于两个矩阵 S w − 1 S b S_w^{-1}S_b Sw−1Sb的特征值 λ \lambda λ和特征向量 w w w的求解,最后推出 w w w的计算方法:
w ∗ = a r g m a x w J ( w ) = a r g m a x w ( w T S b w w T S w w ) = S w − 1 ( μ 1 − μ 2 ) \begin{aligned} w^*&=\mathop{argmax} \limits_{w}\ J(w)\\ &=\mathop{argmax} \limits_{w}\ \left(\frac{w^T\bold S_b w}{w^T\bold S_w w} \right)\\ &=S_w^{-1}(\mu_1-\mu_2) \end{aligned} w∗=wargmax J(w)=wargmax (wTSwwwTSbw)=Sw−1(μ1−μ2)
这个公式尝试告诉我们保留最大的特征值。说实话,有些地方还是无法完全看懂,对于工程实施来说,似乎得到了追去 w w w方法。
看例子
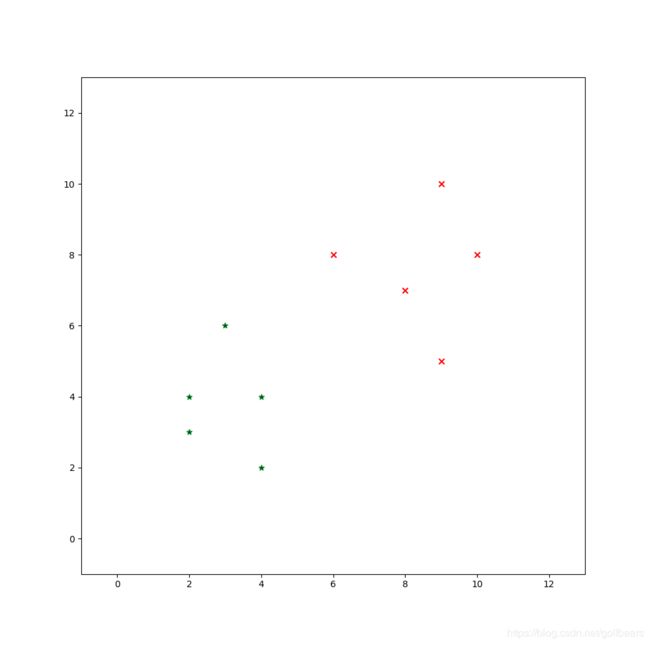
这个例子依旧来自参考文献【2】,这是一个两维散点数据集:
c l a s s 1 : X 1 = ( x 1 , x 2 ) = { ( 4 , 2 ) , ( 2 , 4 ) , ( 2 , 3 ) , ( 3 , 6 ) , ( 4 , 4 ) } c l a s s 2 : X 2 = ( x 1 , x 2 ) = { ( 9 , 10 ) , ( 6 , 8 ) , ( 9 , 5 ) , ( 8 , 7 ) , ( 10 , 8 ) } \begin{aligned} &class1:\bold X_1=(x_1,x_2)=\{(4,2),(2,4),(2,3),(3,6),(4,4) \} \\ &class2:\bold X_2=(x_1,x_2)=\{(9,10),(6,8),(9,5),(8,7),(10,8) \} \end{aligned} class1:X1=(x1,x2)={(4,2),(2,4),(2,3),(3,6),(4,4)}class2:X2=(x1,x2)={(9,10),(6,8),(9,5),(8,7),(10,8)}
讲这些点画在图上
类均值
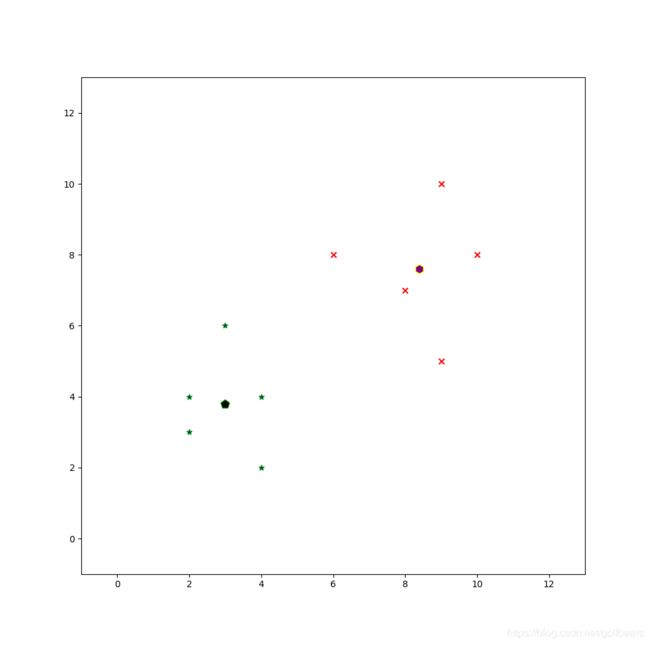
c l a s s 1 : μ 1 = 1 N 1 ∑ x ∈ c l a s s 1 x = 1 5 [ ( 4 2 ) , ( 2 4 ) , ( 2 3 ) , ( 3 6 ) , ( 4 4 ) ] = ( 3 3.8 ) c l a s s 2 : μ 2 = 1 N 1 ∑ x ∈ c l a s s 2 x = 1 5 [ ( 9 10 ) , ( 6 8 ) , ( 9 5 ) , ( 8 7 ) , ( 10 8 ) ] = ( 8.4 7.6 ) \begin{aligned} &class1:\mu_1=\frac{1}{N_1}\sum_{x \in class1}x=\frac{1}{5}\left[\begin{pmatrix}4\\2\end{pmatrix},\begin{pmatrix}2\\4\end{pmatrix},\begin{pmatrix}2\\3\end{pmatrix},\begin{pmatrix}3\\6\end{pmatrix},\begin{pmatrix}4\\4\end{pmatrix} \right]=\begin{pmatrix}3\\3.8\end{pmatrix} \\ &class2:\mu_2=\frac{1}{N_1}\sum_{x \in class2}x=\frac{1}{5}\left[\begin{pmatrix}9\\10\end{pmatrix},\begin{pmatrix}6\\8\end{pmatrix},\begin{pmatrix}9\\5\end{pmatrix},\begin{pmatrix}8\\7\end{pmatrix},\begin{pmatrix}10\\8\end{pmatrix} \right]=\begin{pmatrix}8.4\\7.6\end{pmatrix} \end{aligned} class1:μ1=N11x∈class1∑x=51[(42),(24),(23),(36),(44)]=(33.8)class2:μ2=N11x∈class2∑x=51[(910),(68),(95),(87),(108)]=(8.47.6)
这时候可以看均值在二维坐标系的位置
类协方差矩阵
S 1 = ∑ x ∈ c l a s s 1 ( x − μ 1 ) ( x − μ 1 ) T = [ ( 4 2 ) − ( 3 3.8 ) ] [ ( 4 2 ) − ( 3 3.8 ) ] T + [ ( 2 4 ) − ( 3 3.8 ) ] [ ( 2 4 ) − ( 3 3.8 ) ] T + . . . = ( 1 − 0.25 − 0.25 2.2 ) \begin{aligned} S_1&=\sum_{x \in class1}(\bold{x}-\bold{\mu_1})(\bold{x}-\bold{\mu_1})^T\\ &=\left[\begin{pmatrix}4\\2\end{pmatrix}-\begin{pmatrix}3\\3.8\end{pmatrix}\right]\left[\begin{pmatrix}4\\2\end{pmatrix}-\begin{pmatrix}3\\3.8\end{pmatrix}\right]^T+ \left[\begin{pmatrix}2\\4\end{pmatrix}-\begin{pmatrix}3\\3.8\end{pmatrix}\right]\left[\begin{pmatrix}2\\4\end{pmatrix}-\begin{pmatrix}3\\3.8\end{pmatrix}\right]^T+...\\ &=\begin{pmatrix}1&-0.25\\-0.25&2.2\end{pmatrix} \end{aligned} S1=x∈class1∑(x−μ1)(x−μ1)T=[(42)−(33.8)][(42)−(33.8)]T+[(24)−(33.8)][(24)−(33.8)]T+...=(1−0.25−0.252.2)
S 2 = ∑ x ∈ c l a s s 2 ( x − μ 2 ) ( x − μ 2 ) T = [ ( 9 10 ) − ( 8.4 7.6 ) ] [ ( 9 10 ) − ( 8.4 7.6 ) ] T + [ ( 6 8 ) − ( 8.4 7.6 ) ] [ ( 6 8 ) − ( 8.4 7.6 ) ] T + . . . = ( 2.3 − 0.05 − 0.05 3.3 ) \begin{aligned} S_2&=\sum_{x \in class2}(\bold{x}-\bold{\mu_2})(\bold{x}-\bold{\mu_2})^T\\ &=\left[\begin{pmatrix}9\\10\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]\left[\begin{pmatrix}9\\10\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]^T+ \left[\begin{pmatrix}6\\8\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]\left[\begin{pmatrix}6\\8\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]^T+...\\ &=\begin{pmatrix}2.3&-0.05\\-0.05&3.3\end{pmatrix} \end{aligned} S2=x∈class2∑(x−μ2)(x−μ2)T=[(910)−(8.47.6)][(910)−(8.47.6)]T+[(68)−(8.47.6)][(68)−(8.47.6)]T+...=(2.3−0.05−0.053.3)
类内散度矩阵
S w = S 1 + S 2 = ( 1 − 0.25 − 0.25 2.2 ) + ( 1 − 0.25 − 0.25 2.2 ) = ( 3.3 − 0.3 − 0.3 5.5 ) \begin{aligned} S_w=S_1+S_2&=\begin{pmatrix}1&-0.25\\-0.25&2.2\end{pmatrix}+\begin{pmatrix}1&-0.25\\-0.25&2.2\end{pmatrix}\\ &=\begin{pmatrix}3.3&-0.3\\-0.3&5.5\end{pmatrix} \end{aligned} Sw=S1+S2=(1−0.25−0.252.2)+(1−0.25−0.252.2)=(3.3−0.3−0.35.5)
类间散度矩阵
S b = ∑ ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T = [ ( 3 3.8 ) − ( 8.4 7.6 ) ] [ ( 3 3.8 ) − ( 8.4 7.6 ) ] T = ( 29.16 20.52 20.52 14.44 ) \begin{aligned} S_b&=\sum(\bold{\mu_1}-\bold{\mu_2})(\bold{\mu_1}-\bold{\mu_2})^T\\ &=\left[\begin{pmatrix}3\\3.8\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]\left[\begin{pmatrix}3\\3.8\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]^T\\ &=\begin{pmatrix}29.16&20.52\\20.52&14.44\end{pmatrix} \end{aligned} Sb=∑(μ1−μ2)(μ1−μ2)T=[(33.8)−(8.47.6)][(33.8)−(8.47.6)]T=(29.1620.5220.5214.44)
求解特征值和特征向量
回想上面的公式:
S w − 1 S b w = λ w ⇒ ∣ S w − 1 S b − λ I ∣ = 0 \begin{aligned} & S_w^{-1}S_bw =\lambda w\\ \Rightarrow &|S_w^{-1}S_b -\lambda I|=0 \end{aligned} ⇒Sw−1Sbw=λw∣Sw−1Sb−λI∣=0
带入两个矩阵的值
⇒ ∣ ( 3.3 − 0.3 − 0.3 5.5 ) − 1 ( 29.16 20.52 20.52 14.44 ) − λ ( 1 0 0 1 ) ∣ = 0 ⇒ ∣ ( 0.3045 0.0166 0.0166 0.1827 ) ( 29.16 20.52 20.52 14.44 ) − λ ( 1 0 0 1 ) ∣ = 0 ⇒ ∣ ( 9.2213 − λ 6.489 4.2339 2.9794 − λ ) ∣ = 0 ⇒ ( 9.2213 − λ ) ( 2.9794 − λ ) − 6.489 ∗ 4.2339 = 0 ⇒ λ 1 = 0 , λ 2 = 12.2007 \begin{aligned} \Rightarrow &\left |\begin{pmatrix}3.3&-0.3\\-0.3&5.5\end{pmatrix}^{-1}\begin{pmatrix}29.16&20.52\\20.52&14.44\end{pmatrix} -\lambda\begin{pmatrix}1&0\\0&1\end{pmatrix} \right |=0\\ \Rightarrow &\left |\begin{pmatrix}0.3045&0.0166\\0.0166&0.1827\end{pmatrix}\begin{pmatrix}29.16&20.52\\20.52&14.44\end{pmatrix} -\lambda\begin{pmatrix}1&0\\0&1\end{pmatrix} \right |=0\\ \Rightarrow &\left |\begin{pmatrix}9.2213-\lambda&6.489\\4.2339&2.9794-\lambda\end{pmatrix} \right |=0\\ \Rightarrow &(9.2213-\lambda)(2.9794-\lambda)-6.489*4.2339=0\\ \Rightarrow &\lambda_1=0, \ \lambda_2=12.2007 \end{aligned} ⇒⇒⇒⇒⇒∣∣∣∣∣(3.3−0.3−0.35.5)−1(29.1620.5220.5214.44)−λ(1001)∣∣∣∣∣=0∣∣∣∣(0.30450.01660.01660.1827)(29.1620.5220.5214.44)−λ(1001)∣∣∣∣=0∣∣∣∣(9.2213−λ4.23396.4892.9794−λ)∣∣∣∣=0(9.2213−λ)(2.9794−λ)−6.489∗4.2339=0λ1=0, λ2=12.2007
特征值解出来了,继续解特征向量
( 9.2213 6.489 4.2339 2.9794 ) w 1 = λ w 1 , λ 1 = 0 ⇒ ( 9.2213 6.489 4.2339 2.9794 ) w 1 = 0 w 1 ⇒ w 1 = ( − 0.5755 0.8178 ) \begin{aligned} &\begin{pmatrix}9.2213&6.489\\4.2339&2.9794\end{pmatrix} w_1=\lambda w_1\ , \ \lambda_1=0\\ \Rightarrow &\begin{pmatrix}9.2213&6.489\\4.2339&2.9794\end{pmatrix} w_1=0 w_1\\ \Rightarrow &w_1= \begin{pmatrix}-0.5755\\0.8178\end{pmatrix} \end{aligned} ⇒⇒(9.22134.23396.4892.9794)w1=λw1 , λ1=0(9.22134.23396.4892.9794)w1=0w1w1=(−0.57550.8178)
同理求出
w 2 = ( 0.9088 0.4173 ) w_2= \begin{pmatrix}0.9088\\0.4173\end{pmatrix} w2=(0.90880.4173)
利用上文的另外一个公式
w ∗ = a r g m a x w J ( w ) = a r g m a x w ( w T S b w w T S w w ) = S w − 1 ( μ 1 − μ 2 ) = ( 3.3 − 0.3 − 0.3 5.5 ) − 1 [ ( 3 3.8 ) − ( 8.4 7.6 ) ] = ( 0.3045 0.0166 0.0166 0.1827 ) ( − 5.4 − 3.8 ) = ( 0.9088 0.4173 ) \begin{aligned} w^*&=\mathop{argmax} \limits_{w}\ J(w)\\ &=\mathop{argmax} \limits_{w}\ \left(\frac{w^T\bold S_b w}{w^T\bold S_w w} \right)\\ &=S_w^{-1}(\mu_1-\mu_2)\\ &=\begin{pmatrix}3.3&-0.3\\-0.3&5.5\end{pmatrix}^{-1}\left[\begin{pmatrix}3\\3.8\end{pmatrix}-\begin{pmatrix}8.4\\7.6\end{pmatrix}\right]\\ &=\begin{pmatrix}0.3045&0.0166\\0.0166&0.1827\end{pmatrix}\begin{pmatrix}-5.4\\-3.8\end{pmatrix}\\ &=\begin{pmatrix}0.9088\\0.4173\end{pmatrix} \end{aligned} w∗=wargmax J(w)=wargmax (wTSwwwTSbw)=Sw−1(μ1−μ2)=(3.3−0.3−0.35.5)−1[(33.8)−(8.47.6)]=(0.30450.01660.01660.1827)(−5.4−3.8)=(0.90880.4173)
有了 w ∗ w^* w∗,就可以进行线性变化,这个线性变化带有判别性质,其实在进行计算的初期已经有先验知识,分了两个类,这个是LDA中的分类原理。文献还有映射和pdf分析,篇幅长,暂时不去细嚼了,以后再说。
多分类LDA的推导
上文中第一个例子是三个产地(3分类)的葡萄酒,最后构建出LDA模型,用2维数据可以跟好的区分开来,其实这不是巧合,而是经典的LDA规律。而2维的数学例子最后降维到1维,其实是来自2分类的初始设计,这种降维的理念有点绕。【1】若将 W 视为一个投影矩阵,则N个分类 LDA 将样本投影到 N-1 维空间,N-1 通常远小子数据原有的属性数.于是,可通过这个投影来减小样本点的维数,且投影过程中使用了类别信息?因此LDA也常被视为一种经典的监督降降维技术。由此我们在应用和设计LDA模型的时候要牢记这个规律。而西瓜书的数学推导第一句就让我万劫不复了,所以还是顺着【2】的思路走下去。
假设我们有 n n n维特征向量 X X X对 C C C个类别做鉴别Discriminate,我们需要通过LDA设计一个新的映射,希望这个 n n n维向量降维到 C C C-1维特征向量,同时测试集数据经过变换以后更加容易区分,所以我们引入下面的变换:
y i = w i T x y_i=w_i^Tx yi=wiTx
上式中 w i T w_i^T wiT是一个n维向量,可以将 x x x转换为一个值 y y y,我们需要设计 C C C-1个这样的向量,有这些向量构成向量矩阵:
W = [ w 1 ∣ w 2 ∣ . . . ∣ w c − 1 ] \bold W=\left [w1|w2|...|w_{c-1} \right ] W=[w1∣w2∣...∣wc−1]
那么映射矩阵,或者所谓的投影矩阵来了:
y i = W T x , x = [ x 1 . . x n ] , y = [ y 1 . . y c − 1 ] \begin{aligned} y_i=\bold W^Tx, \ x=\begin{bmatrix}x_1\\.\\.\\x_n\end{bmatrix}, \ y=\begin{bmatrix}y_1\\.\\.\\y_{c-1}\end{bmatrix} \end{aligned} yi=WTx, x=⎣⎢⎢⎡x1..xn⎦⎥⎥⎤, y=⎣⎢⎢⎡y1..yc−1⎦⎥⎥⎤
畅想一下我们有海量的数据集合,用m来表示个数吧,用投影矩阵一样可以转换到另外一个空间:
Y = W T X , X = { [ x 1 1 . . x n 1 ] [ x 1 2 . . x n 2 ] . . . [ x 1 m . . x n m ] } , Y = { [ y 1 1 . . y n 1 ] [ y 1 2 . . y n 2 ] . . . [ y 1 m . . y n m ] } \begin{aligned} \bold Y=\bold W^T\bold X, \ X=\left\{ \begin{bmatrix}x_1^1\\.\\.\\x_n^1\end{bmatrix} \begin{bmatrix}x_1^2\\.\\.\\x_n^2\end{bmatrix}...\begin{bmatrix}x_1^m\\.\\.\\x_n^m\end{bmatrix} \right\}, Y=\left\{ \begin{bmatrix}y_1^1\\.\\.\\y_n^1\end{bmatrix} \begin{bmatrix}y_1^2\\.\\.\\y_n^2\end{bmatrix}...\begin{bmatrix}y_1^m\\.\\.\\y_n^m\end{bmatrix} \right\} \end{aligned} Y=WTX, X=⎩⎪⎪⎨⎪⎪⎧⎣⎢⎢⎡x11..xn1⎦⎥⎥⎤⎣⎢⎢⎡x12..xn2⎦⎥⎥⎤...⎣⎢⎢⎡x1m..xnm⎦⎥⎥⎤⎭⎪⎪⎬⎪⎪⎫,Y=⎩⎪⎪⎨⎪⎪⎧⎣⎢⎢⎡y11..yn1⎦⎥⎥⎤⎣⎢⎢⎡y12..yn2⎦⎥⎥⎤...⎣⎢⎢⎡y1m..ynm⎦⎥⎥⎤⎭⎪⎪⎬⎪⎪⎫
构想已经打好,剩下的就是如何实现了,一切都是依据二维推导,一点一点引伸到多维空间。
类内散度矩阵
看看这个二分类的类内散度矩阵
S w = S 1 + S 2 \begin{aligned} S_w=S_1+S_2 \end{aligned} Sw=S1+S2
在C类空间可以扩展为:
S w = ∑ i = 1 C S i , S i = ∑ x ∈ c l a s s i ( x − μ i ) ( x − μ i ) T , μ i = 1 N i ∑ x ∈ c l a s s i x \begin{aligned} S_w=\sum_{i=1}^CS_i, \ S_i=\sum_{x \in class_i}(x-\mu_i)(x-\mu_i)^T, \mu_i=\frac{1}{N_i}\sum_{x \in class_i}x \end{aligned} Sw=i=1∑CSi, Si=x∈classi∑(x−μi)(x−μi)T,μi=Ni1x∈classi∑x
类间散度矩阵
相比二分类的类间散度矩阵
S b = ∑ ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T \begin{aligned} S_b&=\sum(\bold{\mu_1}-\bold{\mu_2})(\bold{\mu_1}-\bold{\mu_2})^T\\ \end{aligned} Sb=∑(μ1−μ2)(μ1−μ2)T
在C类空间,定义这样一种方式来衡量不同类别的离散程度。
S b = ∑ i = 1 C N i ( μ i − μ ) ( μ i − μ ) T μ = 1 N ∑ ∀ x x = 1 N ∑ ∀ x N i μ i , μ i = 1 N i ∑ x ∈ c l a s s i x \begin{aligned} S_b&=\sum_{i=1}^CN_i(\bold{\mu_i}-\bold{\mu})(\bold{\mu_i}-\bold{\mu})^T\\ \mu&=\frac{1}{N}\sum_{\forall x}x=\frac{1}{N}\sum_{\forall x}N_i\mu_i,\ \ \mu_i=\frac{1}{N_i}\sum_{x \in class_i}x \end{aligned} Sbμ=i=1∑CNi(μi−μ)(μi−μ)T=N1∀x∑x=N1∀x∑Niμi, μi=Ni1x∈classi∑x
投影空间
类内均值和空间均值
μ i ~ = 1 N i ∑ y ∈ c l a s s i y \begin{aligned} \tilde{\mu_i}=\frac{1}{N_i}\sum_{y \in class_i}y \end{aligned} μi~=Ni1y∈classi∑y
μ ~ = 1 N ∑ ∀ y y \begin{aligned} \tilde{\mu}&=\frac{1}{N}\sum_{\forall y}y \end{aligned} μ~=N1∀y∑y
散度矩阵
S w ~ = ∑ i = 1 C S i ~ = ∑ i = 1 C ∑ y ∈ c l a s s i ( y − μ i ~ ) ( y − μ i ~ ) T \begin{aligned} \tilde{S_w}=\sum_{i=1}^C\tilde{S_i}=\sum_{i=1}^C\sum_{y \in class_i}(y-\tilde{\mu_i})(y-\tilde{\mu_i})^T \end{aligned} Sw~=i=1∑CSi~=i=1∑Cy∈classi∑(y−μi~)(y−μi~)T
S b ~ = ∑ i = 1 C N i ( μ i ~ − μ ~ ) ( μ i ~ − μ ~ ) T \begin{aligned} \tilde{S_b}&=\sum_{i=1}^CN_i(\bold{\tilde{\mu_i}}-\bold{\tilde{\mu}})(\bold{\tilde{\mu_i}}-\bold{\tilde{\mu}})^T\\ \end{aligned} Sb~=i=1∑CNi(μi~−μ~)(μi~−μ~)T
按照二维空间的方法,我们可以得出两个空间的散度矩阵变换关系:
S w ~ = W T S w W \begin{aligned} \tilde{S_w}=W^T\bold S_w W \end{aligned} Sw~=WTSwW
S b ~ = W T S b W \begin{aligned} \tilde{S_b}&=W^T\bold S_b W \end{aligned} Sb~=WTSbW
照葫芦画瓢构建多维空间的评价函数:
J ( w ) = ∣ S b ~ ∣ ∣ S w ~ ∣ = ∣ W T S b W ∣ ∣ W T S w W ∣ \begin{aligned} J(w)&=\frac {|\tilde{S_b}|}{|\tilde{S_w}|} =\frac {|W^T\bold S_b W|}{|W^T\bold S_w W|} \end{aligned} J(w)=∣Sw~∣∣Sb~∣=∣WTSwW∣∣WTSbW∣
寻求 W ∗ W^* W∗令上式最大化,眼花缭乱的变化不管了,最后
⇒ S w − 1 S b W ∗ = λ W ∗ λ = J ( w ) = S c a l a r \begin{aligned} \Rightarrow & S_w^{-1}S_bW^* =\lambda W^*\\ &\lambda = J(w)=Scalar \end{aligned} ⇒Sw−1SbW∗=λW∗λ=J(w)=Scalar
又变成了求矩阵特征值和特征向量的问题,这多维空间的矩阵运算不得不依靠工具来帮忙了。至此,公式推导就差不多这样吧。
后记
LDA这个学习动力来自一篇论文,可以最后学习下来,发现暂时对我面临的问题帮助不大,不过真的感慨经典的机器学习算法很精妙,文献【5】的实现有空再看吧。
附录
散点图python程序
import numpy as np
import matplotlib.pyplot as plt
X_1 = [(4,2),(2,4),(2,3),(3,6),(4,4)]
X_2 = [(9,10),(6,8),(9,5),(8,7),(10,8)]
fig = plt.figure(figsize=(10, 10))
ax0 = fig.add_subplot(111)
ax0.set_xlim(-1, 13)
ax0.set_ylim(-1, 13)
for x in X_1:
ax0.scatter(x[0],
x[1],
c='b', marker='*', label='class1', edgecolors='green')
for x in X_2:
ax0.scatter(x[0],
x[1],
c='r', marker='x', label='class2', edgecolors='black')
mu1 = np.mean(np.array(X_1),axis=0)
ax0.scatter(mu1[0],
mu1[1],
c='black', marker='p', label='mu_1', edgecolors='green', s=100)
mu2 = np.mean(np.array(X_2),axis=0)
ax0.scatter(mu2[0],
mu2[1],
c='purple', marker='h', label='mu_1', edgecolors='yellow', s=100)
#ax0.legend(loc='upper right')
plt.show()
pass