Codeforces Round #628 (Div. 2) (A~D)
福利场啊…
感谢出题人卡了EF让我这种蒟蒻能上分…
题目链接

向来都是B可能会卡我一会…第一次被A给卡了一会
题目意思是给出一个数x
求出两个数 使两个数ab的最大公约数加最大公倍数等于x
任意输出结果
看完脑子瓦特了…A题直接上数论了吗??
瞬间五六千人过A,我人都傻了…
墨迹半天推了个式子
设res为公约数的话
从1到n枚举a 求出这个数的最大因子假设为res
那必满足 res+a*b/res==x
就是说b必须是res的整数倍…冒着T的风险交了
然后过了。。一遍切B题,一边感叹A题咋都开始变得比以前难了…
赛后看别人交的代码我傻了…不是题目绕是自己憨批了
对于任意大于1的x 1和x-1 gcd=1,lcm=x-1,sum=1+x-1。。。。
我…算是长个记性吧
我的憨批代码
ll fun(ll val)
{
ll ans=1;
ll len=floor(sqrt(val)+0.5);
for(ll i=1;i<=len;i++)
if(val%i==0)
ans=i;
return ans;
}
void solve()
{
ll x;scanf("%lld",&x);
rep(i,1,x)
{
ll res=fun(i);
if((x-res)*res/i%res==0)
{
cout<<i<<" "<<(x-res)*res/i<<endl;
return ;
}
}
}
正解…
void solve()
{
ll x;scanf("%lld",&x);
cout<<"1"<<" "<<x-1<<endl;
}
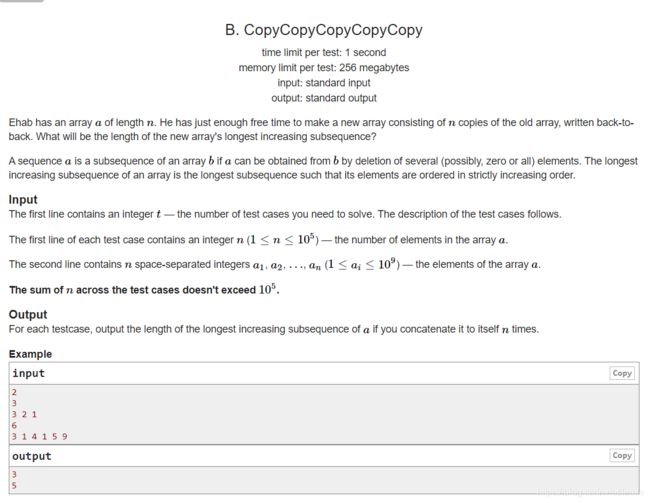
题目简单
copycopycopycopy…
给出一个数组长度为n
你可以扩展n倍 即原来是1,2,3
n=3你可以扩展3倍得到
1,2,3,1,2,3,1,2,3
顺序不能乱 求出最长上升子序列的长度
我们扩展了n倍的话,可以分划为n个区域,每个区域依次找出原数组第一小的,第二小的…
注意不能有相同元素
所以正解是用一个set 自动去重 最后输出set大小即可
void solve()
{
ll n;scanf("%lld",&n);
set<ll>se;
rep(i,1,n)
{
scanf("%lld",&arr[i]);
se.insert(arr[i]);
}
cout<<se.size()<<endl;
}

这道题我半天没读懂…
只知道在写尼姆博弈求SG函数时了解过mex的意义…
差点以为是博弈论的题目…
最后在tip下才读明白

意思大概是
给出你一棵树,但是权值并没有分配
让你构造一种分配的方法来使每一种u–>v
即两个节点的路径所经过的权值mex最大值最小
我先说说mex的含义
mex一个东西,返回值是这个东西里面出现的最小非负整数
即mex(1,3)=0,mex(0,2)=1…
我是贪心做的
在输入时记录每个节点被连接的次数
次数越多代表越多的路径会经过它
那么这时候把这条路径改为最大可以赋予的权值就可以使整体的mex尽可能小,想想mex的含义自己揣摩揣摩…
因为要求按输入顺序输出
所以我们是两边sort一遍compare节点访问次数来分配权值
一次compare最初的顺序复原
记得输入时用pos记录输入顺序
struct node
{
ll u,v;
ll num;
ll val;
ll pos;
}arr[maxn];
ll n;
ll vis[maxn];
bool cmp(node a,node b)
{
a.num=min(vis[a.u],vis[a.v]);
b.num=min(vis[b.u],vis[b.v]);
return a.num<b.num;
}
bool cmp1(node a,node b)
{
return a.pos<b.pos;
}
void solve()
{
ms(vis,0);
scanf("%lld",&n);
rep(i,1,n-1)
{
scanf("%lld %lld",&arr[i].u,&arr[i].v);
arr[i].pos=i;
vis[arr[i].u]++;
vis[arr[i].v]++;
}
sort(arr+1,arr+n,cmp);
rep(i,1,n-1)
{
arr[i].val=i-1;
}
sort(arr+1,arr+n,cmp1);
rep(i,1,n-1)
{
cout<<arr[i].val<<endl;
}
return ;
}
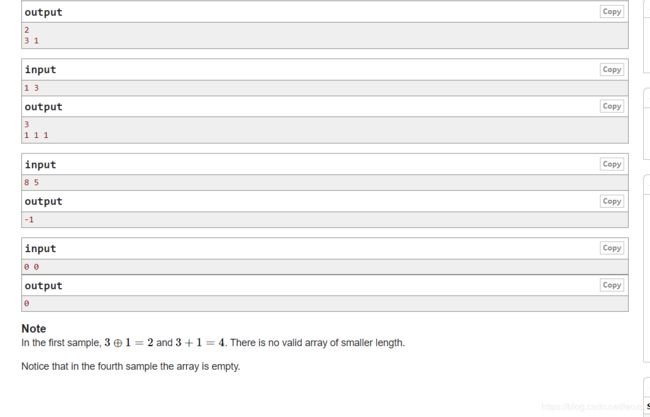
题意很简单
给出两个数u,v,构造出一个数组使得数组内所有元素异或结果为u,相加和为v
要求数组尽可能短(即元素数目尽可能少)
div2我都过了三个题了…算是发挥好的了…抱着随便看看的心态开了D…
结果真a了…破我自己记录了!!div2四题…好谜的比赛啊…
我刚开始的思路是
寻找对于异或和相加的区别,发现二进制状态下 0,0和0,1和1,0和1,1
不论异或还是相加这一位最后的数字两种运算都是一样的!!区别是1,1的话相加需要进一位…然后就没有然后了…发现这并没啥用
之后突然想到
我们最终目的是求出异或为u相加为v,首先一个常识是对于两个数a,b我们假设结果a^b为ans,那么ans一定不会超过原有俩数的最大值即ans<=max(a,b)
具体原因你去在纸上画画异或的过程就明白了
那么我们首先特判
如果u>v那就直接不可能了因为u<=max,v>=max(自己想想)
if(u>v)
{
cout<<"-1"<<endl;
return ;
}
如果u=v那我们就直接输出这个数u就好,但是 注意到样例有一个00的情况需要特判为0,所以我们再加一个特判是否为0即可
if(u==v)
{
if(u==0)
{
cout<<"0"<<endl;
}
else
{
cout<<"1"<<endl<<u<<endl;
}
return ;
}
如果u
我们需要使异或结果为u的话不好确定,但是我们可以把这些数的和v分成
u和v-u两部分 先放入一个u,剩余为res=v-u,之后我们只要使res分成的数异或为0即可
当res为偶数
我们直接均分成res/2,res/2就可以直接异或为0了,满足条件了?但是你会发现第一个样例都过去…因为这个时候还没有满足数目最小
假设此时分成的三个数为u,a,b
a=b; 可以保证异或结果为u,但是数目能不能进一步优化呢?
我们可以尝试着能不能把u和a合并(相加),来进一步限制数目
我们只需要确定u和a合并后会不会对原有异或结果有影响
因为异或是位运算,且0 xor 1=1,1 xor 1=0,0 xor 0=0
所以当a二进制对应的1和u二进制对应的1不冲突就好
换句话说,a二进制为1的地方u不能为1 这个时候一个个模拟就太慢了
用或运算|有奇效 当u,a符合上述条件时 u|a的结果应该和u+a相等
不懂的话在纸上画画二进制相加
那就简单咯
if((a|b)==a+b)
{
cout<<"2"<<endl;
cout<<(a|b)<<" "<<b<<endl;
}
当res为奇数
这种情况我我们可以使u-1让res+1
即 u-1和res+1两部分
这时候需要使res+1异或为1
异或为1最起码要求是最低为为1的数只能有奇数个
但是…res为奇数,那么res+1就是偶数了
偶数的话不论分成几个数,分成的奇数一定是偶数个,偶数最低位为0,
奇数最低位为1,但是奇数有偶数个,所以这种情况不可能~
那就直接上代码吧
void solve()
{
ll u,v;
scanf("%lld %lld",&u,&v);
if(u>v)
{
cout<<"-1"<<endl;
return ;
}
if(u==v)
{
if(u==0)
{
cout<<"0"<<endl;
}
else
{
cout<<"1"<<endl<<u<<endl;
}
return ;
}
ll res=v-u;
if(res%2==0)
{
ll a=u,b=res/2,c=res/2;
if((a|b)==a+b)
{
cout<<"2"<<endl;
cout<<(a|b)<<" "<<b<<endl;
}
else
{
cout<<"3"<<endl;
cout<<u<<" "<<b<<" "<<c<<endl;
}
return ;
}
else
{
cout<<"-1"<<endl;
}
}
其实交D的时候不是很确定,因为我这个算法是在我自己的构造思路下码出来的,不能确定是否有其他的构造方法…
但是D题wa了不亏,ac血赚啊~