AMD Cubemapgen for physically based rendering
JUNE 10, 2012 57 COMMENTS
Version : 1.67 – Living blog – First version was 4 September 2011
AMD Cubemapgen is a useful tool which allow cubemap filtering and mipchain generation. Sadly, AMD decide to stop the support of it. However it has been made open source [1] and has been upload on Google code repository [2] to be improved by community. With some modification, this tool is really useful for physically based rendering because it allow to generate an irradiance environment map (IEM) or a prefiltered mipmaped radiance environment map (PMREM). A PMREM is an environment map (in our case a cubemap) where each mipmap has been filtered by a cosine power lobe of decreasing cosine power value. This post describe such improvement I made for Cubemapgen and few others.
Latest version of Modified Cubemapgen (which include modification describe in this post) are available in the download section of the google code repository. Direct link : ModifiedCubeMapGen-1_66 (require VS2008 runtime and DX9) .
This post will first describe the new features added to Cubemapgen, then for interested (and advanced) readers, I will talk about theory behind the modification and go into some implementation details.
The modified Cubemapgen
The current improvements are under the form of new options accessible in the interface:
(click for full rez)
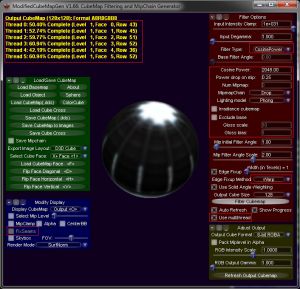
– Use Multithread : Allow to use all hardware threads available on the computer. If uncheck, use the default behavior of Cubemapgen. However new features are unsupported with the default behavior.
– Irradiance Cubemap : Allow a fast computation of an irradiance cubemap. When checked, no other filter or option are take in account. An irradiance cubemap can be get without this option by setting a cosine filter with a Base angle filter of 180 which is a really slow process. Only the base cubemap is affected by this option, the following mipmap use a cosine filter with some default values but these mipmaps should not be used.
– Cosine power filter : Allow to specify a cosine power lobe filter as current filter. It allow to filter the cubemap with a cosine power lobe. You must select this filter to generate a PMREM.
– MipmapChain : Only available with Cosine power filter. Allow to select which mode to use to generate the specular power values used to generate each PMREM’s mipmaps.
– Power drop on mip, Cosine power edit box : Only available with the Drop mode of MipmapChain. Use to generate specular power values used for each PMREM’s mipmaps. The first mipmap will use the cosine power edit box value as cosine power for the cosine power lobe filter. Then the cosine power will be scale by power drop on mip to process the next mipmap and once again this new cosine power will be scale for the next mipmap until all mipmap are generated. For sample, settings 2048 as cosine power edit box and 0.25 as power drop on mip, you will generate a PMREM with each mipmap respectively filtered by cosine power lobe of 2048, 512, 128, 32, 8, 2…
– Num Mipmap, Gloss scale, Gloss bias : Only available with the Mipmap mode of MipmapChain. Use to generate specular power values used for each PMREM’s mipmaps. The value of Num mipmap, Gloss scale and Gloss bias will be used to generate a specular power value for each mipmap.
– Lighting model: This option should be use only with cosine power filter. The choice of the lighting model depends on your game lighting equation. The goal is that the filtering better match your in game lighting.
– Exclude Base : With Cosine power filter, allow to not process the base mimap of the PMREM.
– Warp edge fixup: New edge fixup method which do not used Width based on NVTT from Ignacio Castaño.
– Bent edge fixup: New edge fixup method which do not used Width based on TriAce CEDEC 2011 presentation.
– Strecht edge fixup, FixSeams: New edge fixup method which do not used Width based on NVTT from Ignacio Castaño. FixSeams allow to display PMREM generated with Edge fixup’s Stretch method without seams.
All modification are available in command line (Print usage for detail with “ModifiedCubemapgen.exe – help”).
Irradiance cubemap
Here is a comparison between irradiance map generated with cosine filter of 180 and the option irradiance cubemap (Which use spherical harmonic(SH) for fast processing):
(click for full rez)
Reference
Irradiance cubemap(SH order 5)
Here is a simple shader pseudo-code usage:
float3 AmbientDiffuse = texCube(sampler, WorldSpaceNormal) * c_diffuse;
Prefiltered mipmaped radiance environment map (PMREM)
The cosine power filter allow to apply a convolution with a cosine power (can be call Phong) lobe on the cubemap. There is two methods to generate cosine power values for each PMREM’s mipmaps. Drop and Mipmap. The one to choose depends on you and your engine.
PMREM Drop mode
With the value power drop on mip you can control how fast the cosine power use for convolving each mipmap of the cubemap is decreasing. The radiance come from the fact that cubemap texel store radiance (the incoming lighting).
Here is a simple tutorial of how to generate a prefiltered cubemap mipmap chain:
– Load the base cubemap you want to process ( The loaded cubemap should be HDR (and so in linear space) for best result).
– Chose an output cube texture resolution, we will use 128.
– Chose cosine power filter as filter type.
– Set a value in cosine power edit box. This value will represent the maximum specular power (cosine power and specular power are same thing) you allow for material interacting with this PMREM. We will use 2048 here.
– Chose a power drop on mip, we will use 0.25.
– Click on filter cubemap.
This will generate a PMREM of 8 mipmaps where each mipmap is convolved with a cosine power of respectively:
2048; 512; 128; 32; 8; 2; 0.5; 0.125.
(click for full rez)
The left cross is the loaded cubemap, other are the PMREM, only 5 mipmaps are displayed due to their size (and cubemapgen badly export such crossmap).
There is several way to use such a PMREM in a shader, here I will present you one but remember that you can do as you want.
Our first goal is to define a mapping function which will convert the specular power value of the material on which we will apply the PMREM to a mipmap index. Mipmap index goes from 0 (higher mipmap) to n (smallest mipmap) where n depends on the resolution of the output cubemap:
n = log2(cubemap_size) + 1
In this tutorial we have set cosine power edit box value to 2048. So 2048 is our maximun specular power value for this PMREM. Our mapping function should respect the condition:
MappingFunction(2048) = 0; // 0 is the mipmap index of the base cubemap (first mipmap) MappingFunction(512) = 1; // 1 is the mipmap index of the second mipmap MappingFunction(128) = 2; MappingFunction(32) = 3; MappingFunction(8) = 4; (...)
I do the math for you, the function we are looking for is ![]() or in pseudo code:
or in pseudo code:
float MipmapIndex = log(SpecularPower / MaximunSpecularPower) / log(PowerDropOnMip);
MaximunSpecularPower is the value set in cosine power edit box.
PowerDropOnMip is the value set in power drop on mip.
SpecularPower is the specular power of the material evaluated in the shader.
This formula work perfectly for all PMREMs generated with Modified Cubemapgen and the Drop MipmapChain mode. Whatever the output cubemap resolution you chose, the formula will affect the current material specular power to the mipmap index which best represent it in PMREM. Using this formula for our tutorial values we get:
float MipmapIndex = log(SpecularPower / 2048) / log(0.25);
There is constant values here which can be precomputed. At end we can simplify to a log and a multiply add (which generate 3 instructions: log2 mul madd, log(x) = log(2) * log2(x)):
float MipmapIndex = -0.5 * log2(SpecularPower) + 5.5;
Let’s check the behavior of this code:
-0.5 * log2(2048) + 5.5 = 0 -0.5 * log2(1024) + 5.5 = 0.5 -0.5 * log2(512) + 5.5 = 1 -0.5 * log2(256) + 5.5 = 1.5 -0.5 * log2(128) + 5.5 = 2 -0.5 * log2(64) + 5.5 = 2.5 (...)
This match our constraint well.
We can now sample the PMREM in the shader with the right mipmap index. You must use trilinear filtering for the cubemap sampler. Pseudo-code:
float MipmapIndex = -0.5 * log2(SpecularPower) + 5.5; float3 AmbientSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Disclaimer: Log(0) is undefined. You may want to add an epsilon to avoid this case. This will generate a high MipmapIndex for 0 but this will still correct as the mipmap sampled can’t be greater than number of mipmap (n).
PMREM Mipmap mode
In this mode, the cosine power value and its decrease are control by NumMipmap, Gloss scale and Gloss bias values. Gloss scale and Gloss bias refer to two parameters commonly used when decompressing gloss value to specular power in game engine (See Adopting a physically based shading model for an example).
SpecularPower = exp2(GlossScale * Gloss + GlossBias)
Values must match what is used in your game engine. NumMipmap allow to control the number of mipmap in the PMREM you will effectly used in your game engine. This number will determine the specular power value to used for the convolution of a mipmap with the following formula:
Gloss = 1 - CurrentMipIndexProcessed / (NumMipmap - 1); specularPower = exp2(GlossScale * Gloss + GlossBias);
Here is a simple tutorial of how to generate a prefiltered cubemap mipmap chain:
– Load the base cubemap you want to process ( The loaded cubemap should be HDR (and so in linear space) for best result).
– Chose an output cube texture resolution, we will use 128.
– Set NumMipmap, we will use 8 (A 128x128x6 cubemap as 8 mipmap to reach 1x1x6)
– Set values for GlossScale and GlossBias to match your game engine specular power range, we will use 10 and 1 for a range of [2..2048]
– Click on filter cubemap.
This will generate a PMREM of 8 mipmaps where each mipmap is convolved with a cosine power of respectively:
2048; 760.82 ; 282.64; 105; 39; 14.49; 5.38; 2
If instead your game engine don’t handle mipmap 1x1x6 and 2x2x6, you can put 6 in NumMipmap and get the following values:
2048; 512; 128; 32; 8; 2.
Benefit of Mipmap mode over Drop is to automatically match your range of specular power and the number of mipmap allowed with the PMREM generation. The runtime code is also simpler than with Drop :
// Gloss is the [0..1] value from your gloss map not decompressed in specular power float MipmapIndex = (1 - Gloss) * (NumMipmap - 1); float3 AmbientSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Added note:
There is several way to generate the PMREM. Default Cubemapgen behavior is to process the current mipmap with the previous mipmap as input. I made an exception for the cosine power filter which always use the base cubemap as input. This improve the quality but slow the process.
Exclude Base
When enabled, this option will not modify the base mipmap of the PMREM. Mean you have no filtering applyed. But others mipmaps still convolve normally with the right specular power.
Phong / Phong BRDF/ Blinn/ Blinn BRDF
Lighting model selection should be used when modified Cubemapgen use cosine power filter and the choice depends on your game lighting equation. If you used a normalized Phong lighting in your game, i.e ![]() , chose Phong. If you use a normalized Phong BRDF lighting in your game , i.e
, chose Phong. If you use a normalized Phong BRDF lighting in your game , i.e ![]() you should chose Phong BRDF. Same for Blinn and Blinn BRDF. For more details on physically based lighting model check Adopting a physically based shading model. To understand the disappear of
you should chose Phong BRDF. Same for Blinn and Blinn BRDF. For more details on physically based lighting model check Adopting a physically based shading model. To understand the disappear of ![]() in following code see PI or not to PI in game lighting equation.
in following code see PI or not to PI in game lighting equation.
Pseudo-code for a Phong shader:
// Note here that there is no more PI due to punctual light equation float3 DirectSpecular = (SpecularPower + 1) / 2 * pow(dot(R, V), SpecularPower) * c_specular * c_light; float MipmapIndex = -1.66096404744368 * log(SpecularPower) + 5.5; // Note that there is no normalization factor because it is included in the PMREM by cubemapgen // (see theory after) float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Pseudo-code for a Phong BRDF shader:
float3 DirectSpecular = (SpecularPower + 2) / 2 * pow(dot(R, V), SpecularPower ) * dot(N, L) * c_specular * c_light; float MipmapIndex = -1.66096404744368 * log(SpecularPower) + 5.5; float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Actually, for performance reason, only Phong highlight shape can be prefiltered in cubemapgen. The Blinn lighting model is approximate by fitting its highlight shape to a Phong highlight shape. The fitting process is just a modification of the cosine power at the filtering step. Note that you will not be able to match the elongated highlight shape the Blinn lighting model can provide at grazing angle, the fitting only concern the size of the spot highlight shape.
Other BRDF can’t be represented with PMREM generated by Cubemapgen.
Added note:
A cosine power of 0 with a cosine power filter and Phong BRDF will produce an irradiance cubemap.
A cosine power of 1 with a cosine power filter and Phong will produce an irradiance cubemap.
Edge Fixup warp, bent and stretch
ModifiedCubemapGen provide three new edge fixup methods: Bent, Warp and Strecth. These edge fixup methods give better result than old edge fixup method without requiring any tweak. The parameter Width is not use with these new methods. Three methods are provided because depends on cubemap values, one method provides better result than others. For now, Warp is the recommanded method to start with and is the default method. Here is a sample list of image using differents edge fixup method. On each image, spheres are mapped with a cubemap which is from left to right:
– The original cubemap 128x128x6 filtered with a cosine power of 2048
– The mipmap of a specified resolution and cosine power without edge fixup
– The mipmap of a specified resolution and cosine power with Linear edge fixup and Width of 1
– The mipmap of a specified resolution and cosine power with Bent edge fixup
– The mipmap of a specified resolution and cosine power with Warp edge fixup
– A cubemap of 128x128x6 resolution with specifed cosine power use as reference
(Click for full rez)
 Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
 Original cubemap 128x128x6 – Mipmap from mipchain 4x4x6 – Cosine Power 2
Original cubemap 128x128x6 – Mipmap from mipchain 4x4x6 – Cosine Power 2
 Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
 Original cubemap 128x128x6 – Mipmap from mipchain 2x2x6 – Cosine Power 0.5
Original cubemap 128x128x6 – Mipmap from mipchain 2x2x6 – Cosine Power 0.5
 Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
 Original cubemap 128x128x6 – Mipmap from mipchain 32x32x6 – Cosine Power 128
Original cubemap 128x128x6 – Mipmap from mipchain 32x32x6 – Cosine Power 128
 Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Even if result are subtils, Warp and Bent always perform better or equal than old edge fixup method and don’t depends on Width. It is recommanded to not used old AMD Cubemapgen edge fixup method anymore.
Result of strecht method is not show here. The stretch method purpose is to be used with a specific shader code which allow to fix the seams at runtime as describe by Ignacio Castaño in [10] . Reader should refer to the article for details. If the shader code is not used, the result is less good than with the Warp or Bent method.
To visualize the result of the shader fix seams code from [10] in Modified Cubemapgen, once the PMREM has been filtered with Edge fixup Stretch mode, enable the Select Mip Level on the Modify display panel and enable fix seams:
(Click for full rez)
The pseudo shader code to add is:
// Gloss is the [0..1] value from your gloss map not decompressed in specular power float MipmapIndex = (1 - Gloss) * (NumMipmap - 1); float scale = 1 - exp2(MipmapIndex) / CubemapSize; // CubemapSize is the size of the base mipmap float M = max(max(abs(WorldSpaceReflectionVector.x), abs(WorldSpaceReflectionVector.y)), abs(WorldSpaceReflectionVector.z)); if (abs(WorldSpaceReflectionVector.x) != M) WorldSpaceReflectionVector.x *= scale; if (abs(WorldSpaceReflectionVector.y) != M) WorldSpaceReflectionVector.y *= scale; if (abs(WorldSpaceReflectionVector.z) != M) WorldSpaceReflectionVector.z *= scale; float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Sadly, this code require many instructions: max, exp2, sne, mad, lots of mul and mov representing 4 cycles on PS3.
Added notes:
The shader code work well with the Warp method too.
Theory behind the modification
Prefiltered mipmaped radiance environment map (PMREM)
A cubemap is a way to represent our environment lighting. Each texel in a cubemap (captured from game engine or camera) represent the radiance (incoming lighting) arriving at a single location. The reflectance equation with such environment lighting is defined by :
![]()
To know the output radiance at a given point, we must compute this integral. If the object is perfectly specular (a mirror), a single texel of the cubemap will be required to lit the point. However for glossy or diffuse object, a lot more texels are required. This is a computationally intensive process.
To speed the runtime evaluation, we precompute the integral above and store the result in a cubemap. If we use a Lambertian BRDF for ![]() , we get an irradiance environment map. If we use a Phong or Phong BRDF, we get a PMREM. A PMREM store the reflected light instead of the incoming radiance and is defined for one particular glossiness value.
, we get an irradiance environment map. If we use a Phong or Phong BRDF, we get a PMREM. A PMREM store the reflected light instead of the incoming radiance and is defined for one particular glossiness value.
In case of complex BRDF, like microfacet Blinn BRDF, precomputing the whole integral is not practical due to the large number of input and with a single environment lookup, we are only able to match a Phong lobe shape. This mean that whatever the BRDF shape you have, you must approximate it with a Phong lobe shape. In game we will approximate the evaluation in two parts. We precompute a convolution with a Phong lobe shape in a cubemap (even if we used a Blinn shape lobe as our lighting model) similar to [4]:
![]()
and apply other part of the BRDF (if any, like Fresnel, visibility term) at runtime. Remark that I apply the normalized Phong BRDF as a sample, but you can use normalized Phong depends on your game lighting equation.
The new features added to Cubemapgen allow to generate such a PMREM. The Phong BRDF option allows to specify if you want used a Phong BRDF of just a Phong as lobe shape. Cubemapgen will apply the normalized factor of Phong or Phong BRDF automatically at the PMREM generation, so you don’t need to apply them at runtime.
Lighting model Phong/Blinn
As explain above we must approximate a Blinn lobe shape with a Phong lobe shape if we want to use a Blinn lighting model. Only the spot highlight shape of a Blinn lighting model can be approximate. This two lighting model are related by the relationship (See Relationship between Phong and Blinn lighting model for details):
![]()
Irradiance environment map
It is usual in a game to approximate distant diffuse lighting with an irradiance environment map. This subject has been covered by many and will not be discuss here. The common speed-up today to perform an irradiance environment map is to capture a cubemap, project it in spherical harmonic (SH), apply the cosine convolution then recreate a cubemap from the SH coefficient. This was describe first in [5]. A Gpu approach is also describe in [3].
Normalization factor
Cubemapgen apply the energy conserving factor linked to the filter type in the cubemap result. This mean that for irradiance cubemap you don’t need to divide irradiance to radiance (The factor ![]() ) and for prefiltered radiance environment map you don’t need to deal with the
) and for prefiltered radiance environment map you don’t need to deal with the ![]() or
or ![]() factor.
factor.
Implementation detail
Source code for this modified Cubemapgen are submit on the google code repository http://code.google.com/p/cubemapgen/ which can be browse online. All changed from the original source code are tagged with BEGIN / END. As seeing code often help to the understanding of features, here is some implementation details.
An update of the code I do which affect cubemap processing is the calcul of the solid angle of a cubemap texel. The default Cubemapgen approximation can be improved with this code (Thanks to Ignacio Castaño for it) :
/** Original code from Ignacio Castaño
* This formula is from Manne Öhrström's thesis.
* Take two coordiantes in the range [-1, 1] that define a portion of a
* cube face and return the area of the projection of that portion on the
* surface of the sphere.
**/
static float32 AreaElement( float32 x, float32 y )
{
return atan2(x * y, sqrt(x * x + y * y + 1));
}
float32 TexelCoordSolidAngle(int32 a_FaceIdx, float32 a_U, float32 a_V, int32 a_Size)
{
//scale up to [-1, 1] range (inclusive), offset by 0.5 to point to texel center.
float32 U = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
float32 V = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
float32 InvResolution = 1.0f / a_Size;
// U and V are the -1..1 texture coordinate on the current face.
// Get projected area for this texel
float32 x0 = U - InvResolution;
float32 y0 = V - InvResolution;
float32 x1 = U + InvResolution;
float32 y1 = V + InvResolution;
float32 SolidAngle = AreaElement(x0, y0) - AreaElement(x0, y1) - AreaElement(x1, y0) + AreaElement(x1, y1);
return SolidAngle;
}
Detailed derivation of this result by Rory Driscoll can be found here [7].
Lighting model Phong/Blinn
As explain in theory section, there is a 4 factor which link a Blinn and a Phong lobe shape. This mean that we can generate PMREM to better match Blinn lobe shape when not elongated by dividing its cosine power by 4 before the filtering process:
inline float32 GetSpecularPowerFactorToMatchPhong(float32 SpecularPower)
{
return 4.0f;
}
float32 RefSpecularPower =
(a_MCO.LightingModel == CP_LIGHTINGMODEL_BLINN || a_MCO.LightingModel == CP_LIGHTINGMODEL_BLINN_BRDF) ?
a_MCO.SpecularPower / GetSpecularPowerFactorToMatchPhong(a_MCO.SpecularPower) : a_MCO.SpecularPower;
Prefiltered mipmaped radiance environment map (PMREM)
Code added to support a new cosine power filter is:
//solid angle stored in 4th channel of normalizer/solid angle cube map
weight = *(texelVect+3);
// Here we decide if we use a Phong or a Phong BRDF.
// Phong BRDF is jsut the Phong model multiply by the cosine of the lambert law
// so just adding one to specularpower do the trick.
weight *= pow(tapDotProd, (float32)(a_SpecularPower + IsPhongBRDF));
//iterate over channels
for(k=0; k < nSrcChannels; k++) //up to 4 channels
{
dstAccum[k] += weight * *(srcCubeRowStartPtr + srcCubeRowWalk);
srcCubeRowWalk++;
}
The IsPhongBRDF is defined to 1 when PhongBRDF or BlinnBRDF option is enabled and 0 else. As you can see, the added dot(N, L) is factored in the pow.
Normally, we should go through half texels of the cubemap, as describe by the integral in theory section, to compute a value (Base Filter Angle of 180). To speed up the process I calc a BaseFilterAngle based on the specular power which allow to discard insignificant part (Thanks to Ignacio Castaño again for this optimized version).
// We want to find the alpha such that:
// cos(alpha)^cosinePower = epsilon
// That's: acos(epsilon^(1/cosinePower))
const float32 threshold = 0.000001f; // Empirical threshold
float32 Angle = 180.0f;
if (Angle != 0.0f)
{
Angle = acosf(powf(threshold, 1.0f / cosinePower));
Angle *= 180.0f / (float32)CP_PI; // Convert to degree
Angle *= 2.0f; // * 2.0f because cubemapgen divide by 2 later
}
But with very high value in the HDR cubemap, this can bias the result.
Irradiance environment map
For irradiance cubemap I use spherical harmonics(SH) order 5 which mean 25 coefficients. SH order 3 on my test can introduce little error with some HDR cubemaps.
Projecting a cubemap in SH is simple once you get the right formula for solid angle (the one provide above). You can use the D3DXSHProjectCubeMap if you want. I do my own implementation which can help you to avoid to link with D3DX:
for (int32 iFaceIdx = 0; iFaceIdx < 6; iFaceIdx++)
{
for (int32 y = 0; y < SrcSize; y++)
{
normCubeRowStartPtr = &a_NormCubeMap[iFaceIdx].m_ImgData[NormCubeMapNumChannels * (y * SrcSize)];
srcCubeRowStartPtr = &SrcCubeImage[iFaceIdx].m_ImgData[SrcCubeMapNumChannels * (y * SrcSize)];
for (int32 x = 0; x < SrcSize; x++)
{
//pointer to direction and solid angle in cube map associated with texel
texelVect = &normCubeRowStartPtr[NormCubeMapNumChannels * x];
if(a_bUseSolidAngleWeighting == TRUE)
{ //solid angle stored in 4th channel of normalizer/solid angle cube map
weight = *(texelVect+3);
}
else
{ //all taps equally weighted
weight = 1.0;
}
EvalSHBasis(texelVect, SHdir);
// Convert to float64
float64 R = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 0];
float64 G = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 1];
float64 B = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 2];
for (int32 i = 0; i < NUM_SH_COEFFICIENT; i++)
{
SHr[i] += R * SHdir[i] * weight;
SHg[i] += G * SHdir[i] * weight;
SHb[i] += B * SHdir[i] * weight;
}
weightAccum += weight;
}
}
}
//Normalization - 4.0 * CP_PI is the solid angle of a sphere
for (int32 i = 0; i < NUM_SH_COEFFICIENT; ++i)
{
SHr[i] *= 4.0 * CP_PI / weightAccum;
SHg[i] *= 4.0 * CP_PI / weightAccum;
SHb[i] *= 4.0 * CP_PI / weightAccum;
}
And last piece of code, the conversion from SH to cubemap. The goal is just to sample the SH coefficient with the current direction derive from the cubemap pixel. The tricky part here is the band factor you must apply. The scaling factors for each SH band is due to the fact that we process a convolution over the hemisphere in SH (see PI or not to PI in game lighting equation).:
// See Peter-Pike Sloan paper for these coefficients
static float64 SHBandFactor[NUM_SH_COEFFICIENT] = { 1.0,
2.0 / 3.0, 2.0 / 3.0, 2.0 / 3.0,
1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, // The 4 band will be zeroed
- 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0};
for (int32 iFaceIdx = 0; iFaceIdx < 6; iFaceIdx++)
{
for (int32 y = 0; y < DstSize; y++)
{
normCubeRowStartPtr = &a_NormCubeMap[iFaceIdx].m_ImgData[NormCubeMapNumChannels * (y * DstSize)];
dstCubeRowStartPtr = &DstCubeImage[iFaceIdx].m_ImgData[DstCubeMapNumChannels * (y * DstSize)];
for (int32 x = 0; x < DstSize; x++)
{
//pointer to direction and solid angle in cube map associated with texel
texelVect = &normCubeRowStartPtr[NormCubeMapNumChannels * x];
EvalSHBasis(texelVect, SHdir);
// get color value
CP_ITYPE R = 0.0f, G = 0.0f, B = 0.0f;
for (int32 i = 0; i < NUM_SH_COEFFICIENT; ++i)
{
R += (CP_ITYPE)(SHr[i] * SHdir[i] * BandFactor[i]);
G += (CP_ITYPE)(SHg[i] * SHdir[i] * BandFactor[i]);
B += (CP_ITYPE)(SHb[i] * SHdir[i] * BandFactor[i]);
}
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 0] = R;
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 1] = G;
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 2] = B;
}
}
}
Normalization factor
The normalization factor to apply is calculated numerically in Cubemapgen.
When Cubemapgen do a filtering it calc the accumulated sum of the weight of each texel then divide the accumulated color by the accumulated weight
weight *= pow(tapDotProd, (float32)(a_SpecularPower + IsPhongBRDF));
(...)
weightAccum += weight;
(...)
if(weightAccum != 0.0f)
{
for(k=0; k < m_NumChannels; k++)
{
a_DstVal[k] = (float32)(dstAccum[k] / weightAccum);
}
}
Let’s see what will be calculated for a cosine filter of 180. We will accumulate dot(N,L) * texelSolidAngle for the whole hemisphere. The sum of texelSolidAngle must always be 2 * PI as this is the solid angle of the hemisphere. The result of the numerical integration is PI. Which is what we can deduce analytically :
![]()
Derivation of this result can be found in [6]. As you can see, when we calculate an irradiance cubemap, we divide the result by PI, which is what we expect.
Each numerical integration for Phong and Phong BRDF will match the analytic integration we done to calculate the energy conserving factor of Phong or Phong BRDF : ![]() and
and ![]() . Derivation of this result can be found in [6]. So Cubemapgen is energy conserving at the source!
. Derivation of this result can be found in [6]. So Cubemapgen is energy conserving at the source!
Edge fixup
The Bent edge fixup is my interpretation of the work done by TriAce research [9]. The algorithm is describe on slide titled “Bent Phong Filter Kernel”. The slides are actually in Japanese but an english version is available on the TriAce’s web site.
The goal here is not to blend color like in classic AMD edge fixup but to blend normal instead. Warp do this too and this is why these two new methods provide better results.
The algorithm defined an offset angle which will be used to bent the vector from cubemap center to texel center away from the face normal. To get the offset angle, we define a target angle as the angle between the vector from cubemap center to face edge and vector from cubemap center to edge texel . The offset angle is the value linearly interpolate from 0 to target angle based on distance from cubemap center. This allow to have stronger effect at edge and no effect near cubemap center. There is some tweak added to reduced the contribution of the target angle based on cubemap resolution. I chose to perform this code on texel coordinate rather than change normal later like the Warp method. However contrary to Warp, Bent perform a linear interpolation in spherical domain.
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
(...)
else if (a_FixupType == CP_FIXUP_BENT && a_Size > 1)
{
// Method following description of Physically based rendering slides from CEDEC2011 of TriAce
// Get vector at edge
float32 EdgeNormalU[3];
float32 EdgeNormalV[3];
float32 EdgeNormal[3];
float32 EdgeNormalMinusOne[3];
// Recover vector at edge
(...)
// Get vector at (edge - 1)
float32 nvcUEdgeMinus1 = (2.0f * ((float32)(nvcU < 0.0f ? 0 : a_Size-1) + 0.5f) / (float32)a_Size ) - 1.0f;
float32 nvcVEdgeMinus1 = (2.0f * ((float32)(nvcV < 0.0f ? 0 : a_Size-1) + 0.5f) / (float32)a_Size ) - 1.0f;
// Recover vector at (edge - 1)
(...)
// Get angle between the two vector (which is 50% of the two vector presented in the TriAce slide)
float32 AngleNormalEdge = acosf(VM_DOTPROD3(EdgeNormal, EdgeNormalMinusOne));
// Here we assume that high resolution required less offset than small resolution (TriAce based this on blur radius and custom value)
// Start to increase from 50% to 100% target angle from 128x128x6 to 1x1x6
float32 NumLevel = (logf(min(a_Size, 128)) / logf(2)) - 1;
AngleNormalEdge = LERP(0.5 * AngleNormalEdge, AngleNormalEdge, 1.0f - (NumLevel/6) );
float32 factorU = abs((2.0f * ((float32)a_U) / (float32)(a_Size - 1) ) - 1.0f);
float32 factorV = abs((2.0f * ((float32)a_V) / (float32)(a_Size - 1) ) - 1.0f);
AngleNormalEdge = LERP(0.0f, AngleNormalEdge, max(factorU, factorV) );
// Get current vector
(...)
float32 RadiantAngle = AngleNormalEdge;
// Get angle between face normal and current normal. Used to push the normal away from face normal.
float32 AngleFaceVector = acosf(VM_DOTPROD3(sgFace2DMapping[a_FaceIdx][CP_FACEAXIS], a_XYZ));
// Push the normal away from face normal by an angle of RadiantAngle
slerp(a_XYZ, sgFace2DMapping[a_FaceIdx][CP_FACEAXIS], a_XYZ, 1.0f + RadiantAngle / AngleFaceVector);
}
The Warp edge fixup method of ModifiedCubemapgen is based on NVTT implementation [8]. And have similarity with the TriAce research method:
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
if (a_FixupType == CP_FIXUP_WARP && a_Size > 1)
{
// Code from Nvtt : http://code.google.com/p/nvidia-texture-tools/source/browse/trunk/src/nvtt/CubeSurface.cpp
float32 a = powf(float32(a_Size), 2.0f) / powf(float32(a_Size - 1), 3.0f);
nvcU = a * powf(nvcU, 3) + nvcU;
nvcV = a * powf(nvcV, 3) + nvcV;
(...)
The Stretch edge fixup method of ModifiedCubemapgen is based on NVTT implementation [8].
if (a_FixupType == CP_FIXUP_STRETCH && a_Size > 1)
{
// transform from [0..res - 1] to [-1 .. 1], match up edges exactly.
nvcU = (2.0f * (float32)a_U / ((float32)a_Size - 1.0f) ) - 1.0f;
nvcV = (2.0f * (float32)a_V / ((float32)a_Size - 1.0f) ) - 1.0f;
}
else
{
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
}
The last 1x1x6 mipmap of the mipmap chain is the average of the 6 face in both method.
Reference
[1] http://developer.amd.com/archive/gpu/cubemapgen/Pages/default.aspx
[2] http://code.google.com/p/cubemapgen/
[3] King, “Real-Time Computation of Dynamic Irradiance Environment Maps” http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter10.html
[4] McAllister, “Spatial BRDFs” http://http.developer.nvidia.com/GPUGems/gpugems_ch18.html
[5] Ramamoorthi, Hanrahan “An Efficient Representation for Irradiance Environment Maps” http://graphics.stanford.edu/papers/envmap/
[6] Driscoll, “Energy conservation in game” http://www.rorydriscoll.com/2009/01/25/energy-conservation-in-games/
[7] Driscoll, “Cubemap Texel Solid Angle” http://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/
[8] Castaño, http://code.google.com/p/nvidia-texture-tools/source/browse/trunk/src/nvtt/CubeSurface.cpp
[9] Gotanda, “Real-time Physically Based Rendering – Implementation”, http://research.tri-ace.com/Data/cedec2011_RealtimePBR_Implementation.pptx
[10] Castaño, “Seamless Cube Map Filtering”, http://the-witness.net/news/2012/02/seamless-cube-map-filtering/#more-1502
JUNE 10, 2012 57 COMMENTS
Version : 1.67 – Living blog – First version was 4 September 2011
AMD Cubemapgen is a useful tool which allow cubemap filtering and mipchain generation. Sadly, AMD decide to stop the support of it. However it has been made open source [1] and has been upload on Google code repository [2] to be improved by community. With some modification, this tool is really useful for physically based rendering because it allow to generate an irradiance environment map (IEM) or a prefiltered mipmaped radiance environment map (PMREM). A PMREM is an environment map (in our case a cubemap) where each mipmap has been filtered by a cosine power lobe of decreasing cosine power value. This post describe such improvement I made for Cubemapgen and few others.
Latest version of Modified Cubemapgen (which include modification describe in this post) are available in the download section of the google code repository. Direct link : ModifiedCubeMapGen-1_66 (require VS2008 runtime and DX9) .
This post will first describe the new features added to Cubemapgen, then for interested (and advanced) readers, I will talk about theory behind the modification and go into some implementation details.
The modified Cubemapgen
The current improvements are under the form of new options accessible in the interface:
(click for full rez)

– Use Multithread : Allow to use all hardware threads available on the computer. If uncheck, use the default behavior of Cubemapgen. However new features are unsupported with the default behavior.
– Irradiance Cubemap : Allow a fast computation of an irradiance cubemap. When checked, no other filter or option are take in account. An irradiance cubemap can be get without this option by setting a cosine filter with a Base angle filter of 180 which is a really slow process. Only the base cubemap is affected by this option, the following mipmap use a cosine filter with some default values but these mipmaps should not be used.
– Cosine power filter : Allow to specify a cosine power lobe filter as current filter. It allow to filter the cubemap with a cosine power lobe. You must select this filter to generate a PMREM.
– MipmapChain : Only available with Cosine power filter. Allow to select which mode to use to generate the specular power values used to generate each PMREM’s mipmaps.
– Power drop on mip, Cosine power edit box : Only available with the Drop mode of MipmapChain. Use to generate specular power values used for each PMREM’s mipmaps. The first mipmap will use the cosine power edit box value as cosine power for the cosine power lobe filter. Then the cosine power will be scale by power drop on mip to process the next mipmap and once again this new cosine power will be scale for the next mipmap until all mipmap are generated. For sample, settings 2048 as cosine power edit box and 0.25 as power drop on mip, you will generate a PMREM with each mipmap respectively filtered by cosine power lobe of 2048, 512, 128, 32, 8, 2…
– Num Mipmap, Gloss scale, Gloss bias : Only available with the Mipmap mode of MipmapChain. Use to generate specular power values used for each PMREM’s mipmaps. The value of Num mipmap, Gloss scale and Gloss bias will be used to generate a specular power value for each mipmap.
– Lighting model: This option should be use only with cosine power filter. The choice of the lighting model depends on your game lighting equation. The goal is that the filtering better match your in game lighting.
– Exclude Base : With Cosine power filter, allow to not process the base mimap of the PMREM.
– Warp edge fixup: New edge fixup method which do not used Width based on NVTT from Ignacio Castaño.
– Bent edge fixup: New edge fixup method which do not used Width based on TriAce CEDEC 2011 presentation.
– Strecht edge fixup, FixSeams: New edge fixup method which do not used Width based on NVTT from Ignacio Castaño. FixSeams allow to display PMREM generated with Edge fixup’s Stretch method without seams.
All modification are available in command line (Print usage for detail with “ModifiedCubemapgen.exe – help”).
Irradiance cubemap
Here is a comparison between irradiance map generated with cosine filter of 180 and the option irradiance cubemap (Which use spherical harmonic(SH) for fast processing):
(click for full rez)
Reference
Irradiance cubemap(SH order 5)
Here is a simple shader pseudo-code usage:
float3 AmbientDiffuse = texCube(sampler, WorldSpaceNormal) * c_diffuse;
Prefiltered mipmaped radiance environment map (PMREM)
The cosine power filter allow to apply a convolution with a cosine power (can be call Phong) lobe on the cubemap. There is two methods to generate cosine power values for each PMREM’s mipmaps. Drop and Mipmap. The one to choose depends on you and your engine.
PMREM Drop mode
With the value power drop on mip you can control how fast the cosine power use for convolving each mipmap of the cubemap is decreasing. The radiance come from the fact that cubemap texel store radiance (the incoming lighting).
Here is a simple tutorial of how to generate a prefiltered cubemap mipmap chain:
– Load the base cubemap you want to process ( The loaded cubemap should be HDR (and so in linear space) for best result).
– Chose an output cube texture resolution, we will use 128.
– Chose cosine power filter as filter type.
– Set a value in cosine power edit box. This value will represent the maximum specular power (cosine power and specular power are same thing) you allow for material interacting with this PMREM. We will use 2048 here.
– Chose a power drop on mip, we will use 0.25.
– Click on filter cubemap.
This will generate a PMREM of 8 mipmaps where each mipmap is convolved with a cosine power of respectively:
2048; 512; 128; 32; 8; 2; 0.5; 0.125.
(click for full rez)
The left cross is the loaded cubemap, other are the PMREM, only 5 mipmaps are displayed due to their size (and cubemapgen badly export such crossmap).
There is several way to use such a PMREM in a shader, here I will present you one but remember that you can do as you want.
Our first goal is to define a mapping function which will convert the specular power value of the material on which we will apply the PMREM to a mipmap index. Mipmap index goes from 0 (higher mipmap) to n (smallest mipmap) where n depends on the resolution of the output cubemap:
n = log2(cubemap_size) + 1
In this tutorial we have set cosine power edit box value to 2048. So 2048 is our maximun specular power value for this PMREM. Our mapping function should respect the condition:
MappingFunction(2048) = 0; // 0 is the mipmap index of the base cubemap (first mipmap) MappingFunction(512) = 1; // 1 is the mipmap index of the second mipmap MappingFunction(128) = 2; MappingFunction(32) = 3; MappingFunction(8) = 4; (...)
I do the math for you, the function we are looking for is ![]() or in pseudo code:
or in pseudo code:
float MipmapIndex = log(SpecularPower / MaximunSpecularPower) / log(PowerDropOnMip);
MaximunSpecularPower is the value set in cosine power edit box.
PowerDropOnMip is the value set in power drop on mip.
SpecularPower is the specular power of the material evaluated in the shader.
This formula work perfectly for all PMREMs generated with Modified Cubemapgen and the Drop MipmapChain mode. Whatever the output cubemap resolution you chose, the formula will affect the current material specular power to the mipmap index which best represent it in PMREM. Using this formula for our tutorial values we get:
float MipmapIndex = log(SpecularPower / 2048) / log(0.25);
There is constant values here which can be precomputed. At end we can simplify to a log and a multiply add (which generate 3 instructions: log2 mul madd, log(x) = log(2) * log2(x)):
float MipmapIndex = -0.5 * log2(SpecularPower) + 5.5;
Let’s check the behavior of this code:
-0.5 * log2(2048) + 5.5 = 0 -0.5 * log2(1024) + 5.5 = 0.5 -0.5 * log2(512) + 5.5 = 1 -0.5 * log2(256) + 5.5 = 1.5 -0.5 * log2(128) + 5.5 = 2 -0.5 * log2(64) + 5.5 = 2.5 (...)
This match our constraint well.
We can now sample the PMREM in the shader with the right mipmap index. You must use trilinear filtering for the cubemap sampler. Pseudo-code:
float MipmapIndex = -0.5 * log2(SpecularPower) + 5.5; float3 AmbientSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Disclaimer: Log(0) is undefined. You may want to add an epsilon to avoid this case. This will generate a high MipmapIndex for 0 but this will still correct as the mipmap sampled can’t be greater than number of mipmap (n).
PMREM Mipmap mode
In this mode, the cosine power value and its decrease are control by NumMipmap, Gloss scale and Gloss bias values. Gloss scale and Gloss bias refer to two parameters commonly used when decompressing gloss value to specular power in game engine (See Adopting a physically based shading model for an example).
SpecularPower = exp2(GlossScale * Gloss + GlossBias)
Values must match what is used in your game engine. NumMipmap allow to control the number of mipmap in the PMREM you will effectly used in your game engine. This number will determine the specular power value to used for the convolution of a mipmap with the following formula:
Gloss = 1 - CurrentMipIndexProcessed / (NumMipmap - 1); specularPower = exp2(GlossScale * Gloss + GlossBias);
Here is a simple tutorial of how to generate a prefiltered cubemap mipmap chain:
– Load the base cubemap you want to process ( The loaded cubemap should be HDR (and so in linear space) for best result).
– Chose an output cube texture resolution, we will use 128.
– Set NumMipmap, we will use 8 (A 128x128x6 cubemap as 8 mipmap to reach 1x1x6)
– Set values for GlossScale and GlossBias to match your game engine specular power range, we will use 10 and 1 for a range of [2..2048]
– Click on filter cubemap.
This will generate a PMREM of 8 mipmaps where each mipmap is convolved with a cosine power of respectively:
2048; 760.82 ; 282.64; 105; 39; 14.49; 5.38; 2
If instead your game engine don’t handle mipmap 1x1x6 and 2x2x6, you can put 6 in NumMipmap and get the following values:
2048; 512; 128; 32; 8; 2.
Benefit of Mipmap mode over Drop is to automatically match your range of specular power and the number of mipmap allowed with the PMREM generation. The runtime code is also simpler than with Drop :
// Gloss is the [0..1] value from your gloss map not decompressed in specular power float MipmapIndex = (1 - Gloss) * (NumMipmap - 1); float3 AmbientSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Added note:
There is several way to generate the PMREM. Default Cubemapgen behavior is to process the current mipmap with the previous mipmap as input. I made an exception for the cosine power filter which always use the base cubemap as input. This improve the quality but slow the process.
Exclude Base
When enabled, this option will not modify the base mipmap of the PMREM. Mean you have no filtering applyed. But others mipmaps still convolve normally with the right specular power.
Phong / Phong BRDF/ Blinn/ Blinn BRDF
Lighting model selection should be used when modified Cubemapgen use cosine power filter and the choice depends on your game lighting equation. If you used a normalized Phong lighting in your game, i.e ![]() , chose Phong. If you use a normalized Phong BRDF lighting in your game , i.e
, chose Phong. If you use a normalized Phong BRDF lighting in your game , i.e ![]() you should chose Phong BRDF. Same for Blinn and Blinn BRDF. For more details on physically based lighting model check Adopting a physically based shading model. To understand the disappear of
you should chose Phong BRDF. Same for Blinn and Blinn BRDF. For more details on physically based lighting model check Adopting a physically based shading model. To understand the disappear of ![]() in following code see PI or not to PI in game lighting equation.
in following code see PI or not to PI in game lighting equation.
Pseudo-code for a Phong shader:
// Note here that there is no more PI due to punctual light equation float3 DirectSpecular = (SpecularPower + 1) / 2 * pow(dot(R, V), SpecularPower) * c_specular * c_light; float MipmapIndex = -1.66096404744368 * log(SpecularPower) + 5.5; // Note that there is no normalization factor because it is included in the PMREM by cubemapgen // (see theory after) float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Pseudo-code for a Phong BRDF shader:
float3 DirectSpecular = (SpecularPower + 2) / 2 * pow(dot(R, V), SpecularPower ) * dot(N, L) * c_specular * c_light; float MipmapIndex = -1.66096404744368 * log(SpecularPower) + 5.5; float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Actually, for performance reason, only Phong highlight shape can be prefiltered in cubemapgen. The Blinn lighting model is approximate by fitting its highlight shape to a Phong highlight shape. The fitting process is just a modification of the cosine power at the filtering step. Note that you will not be able to match the elongated highlight shape the Blinn lighting model can provide at grazing angle, the fitting only concern the size of the spot highlight shape.
Other BRDF can’t be represented with PMREM generated by Cubemapgen.
Added note:
A cosine power of 0 with a cosine power filter and Phong BRDF will produce an irradiance cubemap.
A cosine power of 1 with a cosine power filter and Phong will produce an irradiance cubemap.
Edge Fixup warp, bent and stretch
ModifiedCubemapGen provide three new edge fixup methods: Bent, Warp and Strecth. These edge fixup methods give better result than old edge fixup method without requiring any tweak. The parameter Width is not use with these new methods. Three methods are provided because depends on cubemap values, one method provides better result than others. For now, Warp is the recommanded method to start with and is the default method. Here is a sample list of image using differents edge fixup method. On each image, spheres are mapped with a cubemap which is from left to right:
– The original cubemap 128x128x6 filtered with a cosine power of 2048
– The mipmap of a specified resolution and cosine power without edge fixup
– The mipmap of a specified resolution and cosine power with Linear edge fixup and Width of 1
– The mipmap of a specified resolution and cosine power with Bent edge fixup
– The mipmap of a specified resolution and cosine power with Warp edge fixup
– A cubemap of 128x128x6 resolution with specifed cosine power use as reference
(Click for full rez)
 Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
 Original cubemap 128x128x6 – Mipmap from mipchain 4x4x6 – Cosine Power 2
Original cubemap 128x128x6 – Mipmap from mipchain 4x4x6 – Cosine Power 2
 Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
 Original cubemap 128x128x6 – Mipmap from mipchain 2x2x6 – Cosine Power 0.5
Original cubemap 128x128x6 – Mipmap from mipchain 2x2x6 – Cosine Power 0.5
 Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
Original cubemap 128x128x6 – Mipmap from mipchain 8x8x6 – Cosine Power 8
 Original cubemap 128x128x6 – Mipmap from mipchain 32x32x6 – Cosine Power 128
Original cubemap 128x128x6 – Mipmap from mipchain 32x32x6 – Cosine Power 128
 Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Original cubemap 128x128x6 – Mipmap from mipchain 16x16x6 – Cosine Power 32
Even if result are subtils, Warp and Bent always perform better or equal than old edge fixup method and don’t depends on Width. It is recommanded to not used old AMD Cubemapgen edge fixup method anymore.
Result of strecht method is not show here. The stretch method purpose is to be used with a specific shader code which allow to fix the seams at runtime as describe by Ignacio Castaño in [10] . Reader should refer to the article for details. If the shader code is not used, the result is less good than with the Warp or Bent method.
To visualize the result of the shader fix seams code from [10] in Modified Cubemapgen, once the PMREM has been filtered with Edge fixup Stretch mode, enable the Select Mip Level on the Modify display panel and enable fix seams:
(Click for full rez)
The pseudo shader code to add is:
// Gloss is the [0..1] value from your gloss map not decompressed in specular power float MipmapIndex = (1 - Gloss) * (NumMipmap - 1); float scale = 1 - exp2(MipmapIndex) / CubemapSize; // CubemapSize is the size of the base mipmap float M = max(max(abs(WorldSpaceReflectionVector.x), abs(WorldSpaceReflectionVector.y)), abs(WorldSpaceReflectionVector.z)); if (abs(WorldSpaceReflectionVector.x) != M) WorldSpaceReflectionVector.x *= scale; if (abs(WorldSpaceReflectionVector.y) != M) WorldSpaceReflectionVector.y *= scale; if (abs(WorldSpaceReflectionVector.z) != M) WorldSpaceReflectionVector.z *= scale; float3 IndirectSpecular = texCubeLod(sampler, float4(WorldSpaceReflectionVector, MipmapIndex)) * c_specular;
Sadly, this code require many instructions: max, exp2, sne, mad, lots of mul and mov representing 4 cycles on PS3.
Added notes:
The shader code work well with the Warp method too.
Theory behind the modification
Prefiltered mipmaped radiance environment map (PMREM)
A cubemap is a way to represent our environment lighting. Each texel in a cubemap (captured from game engine or camera) represent the radiance (incoming lighting) arriving at a single location. The reflectance equation with such environment lighting is defined by :
![]()
To know the output radiance at a given point, we must compute this integral. If the object is perfectly specular (a mirror), a single texel of the cubemap will be required to lit the point. However for glossy or diffuse object, a lot more texels are required. This is a computationally intensive process.
To speed the runtime evaluation, we precompute the integral above and store the result in a cubemap. If we use a Lambertian BRDF for ![]() , we get an irradiance environment map. If we use a Phong or Phong BRDF, we get a PMREM. A PMREM store the reflected light instead of the incoming radiance and is defined for one particular glossiness value.
, we get an irradiance environment map. If we use a Phong or Phong BRDF, we get a PMREM. A PMREM store the reflected light instead of the incoming radiance and is defined for one particular glossiness value.
In case of complex BRDF, like microfacet Blinn BRDF, precomputing the whole integral is not practical due to the large number of input and with a single environment lookup, we are only able to match a Phong lobe shape. This mean that whatever the BRDF shape you have, you must approximate it with a Phong lobe shape. In game we will approximate the evaluation in two parts. We precompute a convolution with a Phong lobe shape in a cubemap (even if we used a Blinn shape lobe as our lighting model) similar to [4]:
![]()
and apply other part of the BRDF (if any, like Fresnel, visibility term) at runtime. Remark that I apply the normalized Phong BRDF as a sample, but you can use normalized Phong depends on your game lighting equation.
The new features added to Cubemapgen allow to generate such a PMREM. The Phong BRDF option allows to specify if you want used a Phong BRDF of just a Phong as lobe shape. Cubemapgen will apply the normalized factor of Phong or Phong BRDF automatically at the PMREM generation, so you don’t need to apply them at runtime.
Lighting model Phong/Blinn
As explain above we must approximate a Blinn lobe shape with a Phong lobe shape if we want to use a Blinn lighting model. Only the spot highlight shape of a Blinn lighting model can be approximate. This two lighting model are related by the relationship (See Relationship between Phong and Blinn lighting model for details):
![]()
Irradiance environment map
It is usual in a game to approximate distant diffuse lighting with an irradiance environment map. This subject has been covered by many and will not be discuss here. The common speed-up today to perform an irradiance environment map is to capture a cubemap, project it in spherical harmonic (SH), apply the cosine convolution then recreate a cubemap from the SH coefficient. This was describe first in [5]. A Gpu approach is also describe in [3].
Normalization factor
Cubemapgen apply the energy conserving factor linked to the filter type in the cubemap result. This mean that for irradiance cubemap you don’t need to divide irradiance to radiance (The factor ![]() ) and for prefiltered radiance environment map you don’t need to deal with the
) and for prefiltered radiance environment map you don’t need to deal with the ![]() or
or ![]() factor.
factor.
Implementation detail
Source code for this modified Cubemapgen are submit on the google code repository http://code.google.com/p/cubemapgen/ which can be browse online. All changed from the original source code are tagged with BEGIN / END. As seeing code often help to the understanding of features, here is some implementation details.
An update of the code I do which affect cubemap processing is the calcul of the solid angle of a cubemap texel. The default Cubemapgen approximation can be improved with this code (Thanks to Ignacio Castaño for it) :
/** Original code from Ignacio Castaño
* This formula is from Manne Öhrström's thesis.
* Take two coordiantes in the range [-1, 1] that define a portion of a
* cube face and return the area of the projection of that portion on the
* surface of the sphere.
**/
static float32 AreaElement( float32 x, float32 y )
{
return atan2(x * y, sqrt(x * x + y * y + 1));
}
float32 TexelCoordSolidAngle(int32 a_FaceIdx, float32 a_U, float32 a_V, int32 a_Size)
{
//scale up to [-1, 1] range (inclusive), offset by 0.5 to point to texel center.
float32 U = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
float32 V = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
float32 InvResolution = 1.0f / a_Size;
// U and V are the -1..1 texture coordinate on the current face.
// Get projected area for this texel
float32 x0 = U - InvResolution;
float32 y0 = V - InvResolution;
float32 x1 = U + InvResolution;
float32 y1 = V + InvResolution;
float32 SolidAngle = AreaElement(x0, y0) - AreaElement(x0, y1) - AreaElement(x1, y0) + AreaElement(x1, y1);
return SolidAngle;
}
Detailed derivation of this result by Rory Driscoll can be found here [7].
Lighting model Phong/Blinn
As explain in theory section, there is a 4 factor which link a Blinn and a Phong lobe shape. This mean that we can generate PMREM to better match Blinn lobe shape when not elongated by dividing its cosine power by 4 before the filtering process:
inline float32 GetSpecularPowerFactorToMatchPhong(float32 SpecularPower)
{
return 4.0f;
}
float32 RefSpecularPower =
(a_MCO.LightingModel == CP_LIGHTINGMODEL_BLINN || a_MCO.LightingModel == CP_LIGHTINGMODEL_BLINN_BRDF) ?
a_MCO.SpecularPower / GetSpecularPowerFactorToMatchPhong(a_MCO.SpecularPower) : a_MCO.SpecularPower;
Prefiltered mipmaped radiance environment map (PMREM)
Code added to support a new cosine power filter is:
//solid angle stored in 4th channel of normalizer/solid angle cube map
weight = *(texelVect+3);
// Here we decide if we use a Phong or a Phong BRDF.
// Phong BRDF is jsut the Phong model multiply by the cosine of the lambert law
// so just adding one to specularpower do the trick.
weight *= pow(tapDotProd, (float32)(a_SpecularPower + IsPhongBRDF));
//iterate over channels
for(k=0; k < nSrcChannels; k++) //up to 4 channels
{
dstAccum[k] += weight * *(srcCubeRowStartPtr + srcCubeRowWalk);
srcCubeRowWalk++;
}
The IsPhongBRDF is defined to 1 when PhongBRDF or BlinnBRDF option is enabled and 0 else. As you can see, the added dot(N, L) is factored in the pow.
Normally, we should go through half texels of the cubemap, as describe by the integral in theory section, to compute a value (Base Filter Angle of 180). To speed up the process I calc a BaseFilterAngle based on the specular power which allow to discard insignificant part (Thanks to Ignacio Castaño again for this optimized version).
// We want to find the alpha such that:
// cos(alpha)^cosinePower = epsilon
// That's: acos(epsilon^(1/cosinePower))
const float32 threshold = 0.000001f; // Empirical threshold
float32 Angle = 180.0f;
if (Angle != 0.0f)
{
Angle = acosf(powf(threshold, 1.0f / cosinePower));
Angle *= 180.0f / (float32)CP_PI; // Convert to degree
Angle *= 2.0f; // * 2.0f because cubemapgen divide by 2 later
}
But with very high value in the HDR cubemap, this can bias the result.
Irradiance environment map
For irradiance cubemap I use spherical harmonics(SH) order 5 which mean 25 coefficients. SH order 3 on my test can introduce little error with some HDR cubemaps.
Projecting a cubemap in SH is simple once you get the right formula for solid angle (the one provide above). You can use the D3DXSHProjectCubeMap if you want. I do my own implementation which can help you to avoid to link with D3DX:
for (int32 iFaceIdx = 0; iFaceIdx < 6; iFaceIdx++)
{
for (int32 y = 0; y < SrcSize; y++)
{
normCubeRowStartPtr = &a_NormCubeMap[iFaceIdx].m_ImgData[NormCubeMapNumChannels * (y * SrcSize)];
srcCubeRowStartPtr = &SrcCubeImage[iFaceIdx].m_ImgData[SrcCubeMapNumChannels * (y * SrcSize)];
for (int32 x = 0; x < SrcSize; x++)
{
//pointer to direction and solid angle in cube map associated with texel
texelVect = &normCubeRowStartPtr[NormCubeMapNumChannels * x];
if(a_bUseSolidAngleWeighting == TRUE)
{ //solid angle stored in 4th channel of normalizer/solid angle cube map
weight = *(texelVect+3);
}
else
{ //all taps equally weighted
weight = 1.0;
}
EvalSHBasis(texelVect, SHdir);
// Convert to float64
float64 R = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 0];
float64 G = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 1];
float64 B = srcCubeRowStartPtr[(SrcCubeMapNumChannels * x) + 2];
for (int32 i = 0; i < NUM_SH_COEFFICIENT; i++)
{
SHr[i] += R * SHdir[i] * weight;
SHg[i] += G * SHdir[i] * weight;
SHb[i] += B * SHdir[i] * weight;
}
weightAccum += weight;
}
}
}
//Normalization - 4.0 * CP_PI is the solid angle of a sphere
for (int32 i = 0; i < NUM_SH_COEFFICIENT; ++i)
{
SHr[i] *= 4.0 * CP_PI / weightAccum;
SHg[i] *= 4.0 * CP_PI / weightAccum;
SHb[i] *= 4.0 * CP_PI / weightAccum;
}
And last piece of code, the conversion from SH to cubemap. The goal is just to sample the SH coefficient with the current direction derive from the cubemap pixel. The tricky part here is the band factor you must apply. The scaling factors for each SH band is due to the fact that we process a convolution over the hemisphere in SH (see PI or not to PI in game lighting equation).:
// See Peter-Pike Sloan paper for these coefficients
static float64 SHBandFactor[NUM_SH_COEFFICIENT] = { 1.0,
2.0 / 3.0, 2.0 / 3.0, 2.0 / 3.0,
1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0, 1.0 / 4.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, // The 4 band will be zeroed
- 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0, - 1.0 / 24.0};
for (int32 iFaceIdx = 0; iFaceIdx < 6; iFaceIdx++)
{
for (int32 y = 0; y < DstSize; y++)
{
normCubeRowStartPtr = &a_NormCubeMap[iFaceIdx].m_ImgData[NormCubeMapNumChannels * (y * DstSize)];
dstCubeRowStartPtr = &DstCubeImage[iFaceIdx].m_ImgData[DstCubeMapNumChannels * (y * DstSize)];
for (int32 x = 0; x < DstSize; x++)
{
//pointer to direction and solid angle in cube map associated with texel
texelVect = &normCubeRowStartPtr[NormCubeMapNumChannels * x];
EvalSHBasis(texelVect, SHdir);
// get color value
CP_ITYPE R = 0.0f, G = 0.0f, B = 0.0f;
for (int32 i = 0; i < NUM_SH_COEFFICIENT; ++i)
{
R += (CP_ITYPE)(SHr[i] * SHdir[i] * BandFactor[i]);
G += (CP_ITYPE)(SHg[i] * SHdir[i] * BandFactor[i]);
B += (CP_ITYPE)(SHb[i] * SHdir[i] * BandFactor[i]);
}
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 0] = R;
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 1] = G;
dstCubeRowStartPtr[(DstCubeMapNumChannels * x) + 2] = B;
}
}
}
Normalization factor
The normalization factor to apply is calculated numerically in Cubemapgen.
When Cubemapgen do a filtering it calc the accumulated sum of the weight of each texel then divide the accumulated color by the accumulated weight
weight *= pow(tapDotProd, (float32)(a_SpecularPower + IsPhongBRDF));
(...)
weightAccum += weight;
(...)
if(weightAccum != 0.0f)
{
for(k=0; k < m_NumChannels; k++)
{
a_DstVal[k] = (float32)(dstAccum[k] / weightAccum);
}
}
Let’s see what will be calculated for a cosine filter of 180. We will accumulate dot(N,L) * texelSolidAngle for the whole hemisphere. The sum of texelSolidAngle must always be 2 * PI as this is the solid angle of the hemisphere. The result of the numerical integration is PI. Which is what we can deduce analytically :
![]()
Derivation of this result can be found in [6]. As you can see, when we calculate an irradiance cubemap, we divide the result by PI, which is what we expect.
Each numerical integration for Phong and Phong BRDF will match the analytic integration we done to calculate the energy conserving factor of Phong or Phong BRDF : ![]() and
and ![]() . Derivation of this result can be found in [6]. So Cubemapgen is energy conserving at the source!
. Derivation of this result can be found in [6]. So Cubemapgen is energy conserving at the source!
Edge fixup
The Bent edge fixup is my interpretation of the work done by TriAce research [9]. The algorithm is describe on slide titled “Bent Phong Filter Kernel”. The slides are actually in Japanese but an english version is available on the TriAce’s web site.
The goal here is not to blend color like in classic AMD edge fixup but to blend normal instead. Warp do this too and this is why these two new methods provide better results.
The algorithm defined an offset angle which will be used to bent the vector from cubemap center to texel center away from the face normal. To get the offset angle, we define a target angle as the angle between the vector from cubemap center to face edge and vector from cubemap center to edge texel . The offset angle is the value linearly interpolate from 0 to target angle based on distance from cubemap center. This allow to have stronger effect at edge and no effect near cubemap center. There is some tweak added to reduced the contribution of the target angle based on cubemap resolution. I chose to perform this code on texel coordinate rather than change normal later like the Warp method. However contrary to Warp, Bent perform a linear interpolation in spherical domain.
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
(...)
else if (a_FixupType == CP_FIXUP_BENT && a_Size > 1)
{
// Method following description of Physically based rendering slides from CEDEC2011 of TriAce
// Get vector at edge
float32 EdgeNormalU[3];
float32 EdgeNormalV[3];
float32 EdgeNormal[3];
float32 EdgeNormalMinusOne[3];
// Recover vector at edge
(...)
// Get vector at (edge - 1)
float32 nvcUEdgeMinus1 = (2.0f * ((float32)(nvcU < 0.0f ? 0 : a_Size-1) + 0.5f) / (float32)a_Size ) - 1.0f;
float32 nvcVEdgeMinus1 = (2.0f * ((float32)(nvcV < 0.0f ? 0 : a_Size-1) + 0.5f) / (float32)a_Size ) - 1.0f;
// Recover vector at (edge - 1)
(...)
// Get angle between the two vector (which is 50% of the two vector presented in the TriAce slide)
float32 AngleNormalEdge = acosf(VM_DOTPROD3(EdgeNormal, EdgeNormalMinusOne));
// Here we assume that high resolution required less offset than small resolution (TriAce based this on blur radius and custom value)
// Start to increase from 50% to 100% target angle from 128x128x6 to 1x1x6
float32 NumLevel = (logf(min(a_Size, 128)) / logf(2)) - 1;
AngleNormalEdge = LERP(0.5 * AngleNormalEdge, AngleNormalEdge, 1.0f - (NumLevel/6) );
float32 factorU = abs((2.0f * ((float32)a_U) / (float32)(a_Size - 1) ) - 1.0f);
float32 factorV = abs((2.0f * ((float32)a_V) / (float32)(a_Size - 1) ) - 1.0f);
AngleNormalEdge = LERP(0.0f, AngleNormalEdge, max(factorU, factorV) );
// Get current vector
(...)
float32 RadiantAngle = AngleNormalEdge;
// Get angle between face normal and current normal. Used to push the normal away from face normal.
float32 AngleFaceVector = acosf(VM_DOTPROD3(sgFace2DMapping[a_FaceIdx][CP_FACEAXIS], a_XYZ));
// Push the normal away from face normal by an angle of RadiantAngle
slerp(a_XYZ, sgFace2DMapping[a_FaceIdx][CP_FACEAXIS], a_XYZ, 1.0f + RadiantAngle / AngleFaceVector);
}
The Warp edge fixup method of ModifiedCubemapgen is based on NVTT implementation [8]. And have similarity with the TriAce research method:
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
if (a_FixupType == CP_FIXUP_WARP && a_Size > 1)
{
// Code from Nvtt : http://code.google.com/p/nvidia-texture-tools/source/browse/trunk/src/nvtt/CubeSurface.cpp
float32 a = powf(float32(a_Size), 2.0f) / powf(float32(a_Size - 1), 3.0f);
nvcU = a * powf(nvcU, 3) + nvcU;
nvcV = a * powf(nvcV, 3) + nvcV;
(...)
The Stretch edge fixup method of ModifiedCubemapgen is based on NVTT implementation [8].
if (a_FixupType == CP_FIXUP_STRETCH && a_Size > 1)
{
// transform from [0..res - 1] to [-1 .. 1], match up edges exactly.
nvcU = (2.0f * (float32)a_U / ((float32)a_Size - 1.0f) ) - 1.0f;
nvcV = (2.0f * (float32)a_V / ((float32)a_Size - 1.0f) ) - 1.0f;
}
else
{
// transform from [0..res - 1] to [- (1 - 1 / res) .. (1 - 1 / res)]
// + 0.5f is for texel center addressing
nvcU = (2.0f * ((float32)a_U + 0.5f) / (float32)a_Size ) - 1.0f;
nvcV = (2.0f * ((float32)a_V + 0.5f) / (float32)a_Size ) - 1.0f;
}
The last 1x1x6 mipmap of the mipmap chain is the average of the 6 face in both method.
Reference
[1] http://developer.amd.com/archive/gpu/cubemapgen/Pages/default.aspx
[2] http://code.google.com/p/cubemapgen/
[3] King, “Real-Time Computation of Dynamic Irradiance Environment Maps” http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter10.html
[4] McAllister, “Spatial BRDFs” http://http.developer.nvidia.com/GPUGems/gpugems_ch18.html
[5] Ramamoorthi, Hanrahan “An Efficient Representation for Irradiance Environment Maps” http://graphics.stanford.edu/papers/envmap/
[6] Driscoll, “Energy conservation in game” http://www.rorydriscoll.com/2009/01/25/energy-conservation-in-games/
[7] Driscoll, “Cubemap Texel Solid Angle” http://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/
[8] Castaño, http://code.google.com/p/nvidia-texture-tools/source/browse/trunk/src/nvtt/CubeSurface.cpp
[9] Gotanda, “Real-time Physically Based Rendering – Implementation”, http://research.tri-ace.com/Data/cedec2011_RealtimePBR_Implementation.pptx
[10] Castaño, “Seamless Cube Map Filtering”, http://the-witness.net/news/2012/02/seamless-cube-map-filtering/#more-1502



