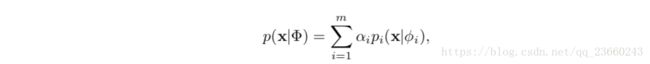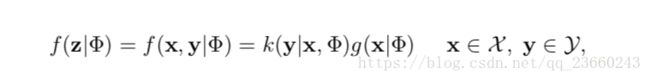EM+GMM

最近在研究HMM底层，想法是能够自己手动实现全部底层部件。包括GMM，Baum-Welch和维特比算法等。刚进入GMM就遇到了很多的坑，这里总算走过一遍，自己也实现了一遍，代码放在我的github地址，感兴趣的可以去看。这里我主要介绍EM和GMM的联合使用，主要是训练阶段，并给出实验结果。

在开始之前，我必须要对几个点说清楚。首先，我不会再跟大家讲解EM算法，因为博客上大家都在讲，不过我认为他们讲的真的太断章取义，拿几个点直接来说没有意义，我们要知道怎么来的，怎么用的，为什么这么用。所以我建议大家看这篇论文：The EM Algorithm in Multivariate Gaussian Mixture Models using Anderson Acceleration，真的非常有帮助。关于EM我认为第一次接触的人明白一下两点就可以：

1. EM和MLE（最大相似估计）的区别？

其实二者最大的区别是前者EM认为后者MLE处理的数据是不完整的。所谓不完整可能指数据本身有缺失，或者有隐藏状态没有表现出来。【再深入？看论文去，再说多就是害你】

2. EM算法核心？

EM主要分为两部分：第一步（也就是E步骤）：确定Q函数  第二步（也就是M步骤）：找到使得Q函数最大的参数。至于细节，看论文去！

关于EM算法我就叙述到这里，下面主要是关于GMM的部分。首先有几个概念要白扯清楚：单高斯，混合高斯，多变量混合高斯。不要懵，其实经过仔细查看就会明白区别，不过鉴于你查看博客而不是查看wiki，所以我认为你想更快的得到他们的区别，那么我用下面的一段话来概括说明他们的区别：

单高斯是一维变量一个模型，混合高斯是一维变量多个模型，多变量混合高斯是多个维度变量多个模型。

还是糊涂？好，那么我再用更浅显的说法叙述一遍。

假设你有一堆数据，比如是人的名字，同时假设有N个。那么你拥有一个N*1维度的初始数据，你可以用一个单高斯模型来模拟他的分布。单高斯如下：

高斯分布：

其图像如下：

ok，到此为止如果有人不明白上述我说的，就可以关闭此博客，去wiki上查看什么叫正态分布或者回去恶补一下概率论等。

那么现在变了，经过我们小组的讨论，一个高斯模型，并不能很好的描述该分布，我们认为多个高斯分布（高斯分布就是正态分布）才能描述样本的分布，所以我们使用混合高斯分布，其公式如下：

让我这样来描述这个公式：假设你有m个模型，也就是说在本分类问题中，你要把N个样本分为m类，每个类用一个高斯分布来描述。那么第一个参数alpha，所有的alpha值的和应该为1，它表明属于各个模型的初始概率【比方说：第一个高斯概率的数据比较多为15，第二个高斯比较少为5，那么m=2的情况下，其初始概率分布为3/4和1/4，仔细想这个问题】。那么其中每个pi都是上面的单高斯模型，要想确定它必须知道均值和方差。

ok假设大家理解了上面的例子，那么我们继续。其实我说原始数据是一维度的是很不切实际的，哪有光记人名字不记电话好吗什么的，现在几乎拿到手的数据至少二维度，所以假设我们一开始的数据是：名字，电话，地址等。那么我们描述样本分布和刚才的第二个例子有什么不同吗？

其实前面都一样的，只不过我们的pi已经不是刚才的单高斯pdf了，而是形如下面的pdf：

那么到此结束我想我已经把关于高斯分布的几种形式表示清楚了。那么我们下面进入GMM的主体，我们假设的使用环境就是上述的第三种情况：多变量混合高斯模型（multivariate GMM ）。

首先要说明，EM算法所起的作用是什么？

EM算法是用来估计参数的。那么问题来了，我们要确定GMM模型，需要确定哪些参数？

一个高斯模型需要确定一个均值和方差，那么混合高斯模型需要确定多个均值和方差，同时还有初始概率分布。那么没错，我们仅仅需要确定这三大类参数我们就确定了GMM模型。

那么同时回想一下EM算法和MLE算法最大的区别和EM算法的核心。那么在看一下我们的概率模型：

这里x表示观测数据（也就是你的多维原始数据），这里的phi表示参数集合，就是我们上面说的均值，方差，和初始概率分布。我们可以假设：x数据是不完整的，缺了y，假设z=（x,y）才是完整数据，所以我们改写似然函数，假如y，这样能够大大简化求解最大似然函数的过程。那么我们当我们知道y的时候，其实似然函数特别容易求解：

具体不求解，不过在真实情况下，y一般是未知的【废话，不然为啥叫隐藏数据呀】。所以我们不能按照上面的MLE的似然函数的套路求解，没错，要换套路了。

换成啥套路了呢？EM的套路呀！EM算法核心是得先确定Q函数呀，所以首要目标确定Q函数。

我们先给出下面两个PDF：

第一个表明在知道参数（均值，方差，初始分布）的请款下，生成该观测数据的概率，第二个表明在如果该观测数据属于y模型，那么最终生成该观测数据序列的概率（很不好理解，确实，没办法，我也没有更好的解释）。

同时根据EM算法我们知道：

所以我们可以得到：

【看到这里上述几个公式大家都应该理解了，如果没有理解可以到论文查看详细过程】。

下面要确定Q函数了，这里我不会为难自己和大家，我不会推，确实不会，大家可以看个初版Q：

所以根据种种条件，我们得到最终的Q如下：

其中，pi为：

完美，跟我们之前说的都一一对应。下面是最大化Q函数，这里不细讲，我只说核心思想（因为细讲了也没用，你最终需要的仅仅是一个更新公式）：利用拉格朗日乘子法，对初始化概率相加为1的条件带入，然后求导数，导数为0.....（我相信我说到这大家都知道后面要做什么了，至于是局部最优解还是全局最优解的问题，作者说了：二阶导数为负数，这就说明了导数在变小，斜率在变小说明是一个凸函数，局部最大即为全局最大）。最终我们得到更新公式如下：

那么到此大家应该明白了GMM算法了。希望跟大家讨论语音方面的问题，所以很早就建了个群：704645273，感兴趣的朋友可以加一下，大家一起进步学习。

我的github地址