MFCC & PLP
我的书:
![]()
淘宝购买链接
当当购买链接
京东购买链接
这在前一篇博客中提到的语音特征提取的常用方法之一。
##MFCC
对于语音/说话人识别,最常用的声学特征是梅尔导谱系数(mel-scale frequency cepstral coefficient,MFCC)。
kaldi 特征提取默认参数设置:
###预加重
将信号通过高通滤波器:
s 2 ( n ) = s ( n ) − a ∗ s ( n − 1 ) s_2(n)=s(n)-a^{*}s(n-1) s2(n)=s(n)−a∗s(n−1)
上式中 s 2 s_2 s2是输出, a a a是滤波器系数,通常取 0.9 ∼ 1 0.9 \sim1 0.9∼1之间,其Z变换是:
H ( z ) = 1 − a ∗ z − 1 H(z)=1-a^{*}z^{-1} H(z)=1−a∗z−1
通常预加重是为了补偿人发声系统对高频部分的抑制,也就是可以放大高频谐振峰的重要性。
waveFile='whatFood.wav';
au=myAudioRead(waveFile);
y=au.signal; fs=au.fs a=0.95;
y2 = filter([1, -a], 1, y);
time=(1:length(y))/fs;
au2=au;
au2.signal=y2;
myAudioWrite(au2, 'whatFood_preEmphasis.wav');
subplot(2,1,1); plot(time, y);
title('Original wave: s(n)');
subplot(2,1,2); plot(time, y2);
title(sprintf('After pre-emphasis:
s_2(n)=s(n)-a*s(n-1), a=%f', a));
subplot(2,1,1); set(gca, 'unit', 'pixel');
axisPos=get(gca, 'position');
uicontrol('string', 'Play', 'position', [axisPos(1:2), 60, 20], 'callback', 'sound(y, fs)');
subplot(2,1,2); set(gca, 'unit', 'pixel');
axisPos=get(gca, 'position');
uicontrol('string', 'Play', 'position', [axisPos(1:2), 60, 20], 'callback', 'sound(y2, fs)');

###分帧
MFCC将语音分为很多帧,每帧长度通常,128,256或,512,涵盖的时间范围通常是 10 m s ∼ 30 m s 10ms\sim30ms 10ms∼30ms,为了避免相邻两帧之间变化过大,通常相邻两帧之间会有重叠,重叠部分约为帧长的 1 / 3 1/3 1/3,以8kHz为例,若帧长取256点,则帧长对于的时间是 ( 256 / 8000 ∗ 1000 ) = 32 m s (256/8000*1000)=32ms (256/8000∗1000)=32ms。
###加窗
将每帧程序汉明窗,加窗的原因是后面做FFT变换时避免频谱混叠问题,否则会产生不存在信号的频谱。以增加帧左右两端的连续性,设帧内信号是 S ( n ) , n = 0 , 1 , . . . , N − 1 S(n),n=0,1,...,N-1 S(n),n=0,1,...,N−1。则乘上汉明窗后为 S ′ ( n ) = S ( n ) ∗ W ( n ) S^{'}(n)=S(n)*W(n) S′(n)=S(n)∗W(n),其中:
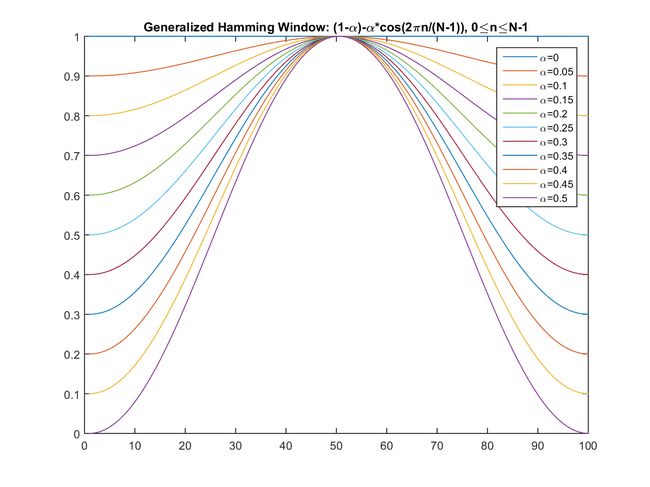
W ( n , a ) = ( 1 − a ) − a cos ( 2 π n / ( N − 1 ) ) , 0 ≤ n ≤ N − 1 W(n,a)=(1-a)-a\cos(2\pi n/(N-1)), 0 \le n \le N-1 W(n,a)=(1−a)−acos(2πn/(N−1)),0≤n≤N−1
不同的a产生不同的汉明窗,通常a取0.46:
feature-window.h
struct FrameExtractionOptions {
BaseFloat samp_freq;
BaseFloat frame_shift_ms; // in milliseconds.
BaseFloat frame_length_ms; // in milliseconds.
BaseFloat dither; // Amount of dithering, 0.0 means no dither.
BaseFloat preemph_coeff; // Preemphasis coefficient.
bool remove_dc_offset; // Subtract mean of wave before FFT.
std::string window_type; // e.g. Hamming window
bool round_to_power_of_two;
BaseFloat blackman_coeff;
bool snip_edges;
// May be "hamming", "rectangular", "povey", "hanning", "blackman"
// "povey" is a window I made to be similar to Hamming but to go to zero at the
// edges, it's pow((0.5 - 0.5*cos(n/N*2*pi)), 0.85)
// I just don't think the Hamming window makes sense as a windowing function.
FrameExtractionOptions():
samp_freq(16000),
frame_shift_ms(10.0),
frame_length_ms(25.0),
dither(1.0),
preemph_coeff(0.97),
remove_dc_offset(true),
window_type("povey"),
round_to_power_of_two(true),
blackman_coeff(0.42),
snip_edges(true){ }
###STFT
语音对应一个频谱(通过短时FFT计算),频谱表示频率与能量的关系。在实际使用中,频谱图有三种,即线性振幅频谱/对数振幅谱/自功率谱(对数振幅谱中各谱线的振幅都作了对数计算,所以其纵坐标的单位是dB(分贝))。这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号)。

S a ′ ( k ) = ∑ n = 0 N − 1 s ′ ( n ) e − j 2 π k / N , 0 ≤ k ≤ N S_a^{'}(k)=\sum_{n=0}^{N-1}s'(n)e^{-j2\pi k/N}, 0 \le k \le N Sa′(k)=∑n=0N−1s′(n)e−j2πk/N,0≤k≤N
###三角带通滤波器
将能量谱城西一组22~26个三角带通滤波器,带通滤波器的中心频率 f ( m ) , m = 1 , 2... f(m), m=1,2... f(m),m=1,2..., f ( m ) f(m) f(m)之间的间隔随着m值的减小而缩小,随着m的增大而加宽。求得每个滤波器输出的对数能量( L o g ( E n e r g y ) Log(Energy) Log(Energy)),这20个三角带通滤波器在“梅尔频谱”上是均匀分布的,梅尔频谱和一般频率 f f f的关系如下:
m e l ( f ) = 2595 ∗ l o g 10 ( 1 + f / 700 ) mel(f)=2595*log_{10}(1+f/700) mel(f)=2595∗log10(1+f/700)
或者
m e l ( f ) = 1125 ∗ l n ( 1 + f / 700 ) mel(f)=1125*ln(1+f/700) mel(f)=1125∗ln(1+f/700)
梅尔频率代表一般人耳对于频率的感受度(人耳对频率f的感受是呈对数变化的)。在低频部分,人耳感受是比较敏锐的,在高频部分,人耳的感受就会越来越粗糙。


三角滤波器的频率相应定义如下:

式中 ∑ m = 0 M − 1 H ) m ( k ) = 1 \sum_{m=0}^{M-1}H)_m(k)=1 ∑m=0M−1H)m(k)=1
三角带通滤波主要有两个目的:
1.对频谱进行平滑,并消除谐波的作用,突出原语音的共振峰。(因此一段语音的音调或音高,是不在MFCC参数内,也就是是以MFCC为特征的语音识别系统,并不收输入语音音调不同而有所影响)
2.减少包函的特征信息量。
###计算每个滤波器组输出的对数能量
S ∗ ( m ) = l n ( ∑ k = 0 N − 1 ∣ S a ′ ( k ) ∣ 2 H m ( k ) ) , 0 ≤ m ≤ M S^*(m)=ln(\sum_{k=0}^{N-1}|S_a^{'}(k)|^2H_m(k)), 0 \le m \le M S∗(m)=ln(∑k=0N−1∣Sa′(k)∣2Hm(k)),0≤m≤M
###离散余弦变换
将上述20个对数能量 E k E_k Ek带入离散余弦变换,求出L阶的Mel导谱系数,通常L取 12 ∼ 16 12\sim 16 12∼16,离散余弦变换公式如下:
C m = ∑ m = 0 N − 1 S m ∗ cos n ∗ ( m − 0.5 ) ∗ π N , m = 1 , 2 , . . . , L C_m=\sum\limits_{m=0}^{N-1}S_{m}^{*}\cos \frac{n*(m-0.5)*\pi}{N}, m=1,2,...,L Cm=m=0∑N−1Sm∗cosNn∗(m−0.5)∗π,m=1,2,...,L
其中 S m ∗ S_{m}^{*} Sm∗是由前一个步计算出来的三角滤波器和频谱能量的内积值,N是三角滤波器的个数。由于之前做过FFT计算,DCT变换是期望转换到时域的,称为Quefrency Domain。其实也就是导谱。又因为之前采用Mel-Frequency来转换至梅尔频谱。
###对数能量
一帧的能量也是语音的重要特征,而且非常容易计算。因此,通常将对数能量做为MFCC的第13个特征。如果需要也可以加上其它特征,如音高(pitch), 过零率和高阶共振峰。
###动态导谱差分参数(Delta cepstrum)
虽然已经求出13个参数,这反映的是静态特性,实际应用于语音识别时,通常会再加上差量导谱参数,以显示语音的动态特性。其意义是导谱参数对时间的变化率:

式中, d t d_t dt表示第t个一阶差分, C t C_t Ct表示第t个导谱系数的系数,Q表示导谱系数的阶数, K表示一阶导数的时间差,可以取1或者2,将上式结果再次带入,可以求得二阶差分参数。这里如果K值取2,如果在加上差量运算,就会产生26维的特征向量;如果同事考虑差量运算就会产生39维特征向量,一般语音识别系统,就是使用这39维的特征向量。

图1 一帧信号的频谱变换
先将其中一帧语音(蓝色)的频谱(红色)通过坐标表示出来,如上图。现在将频谱旋转 90 度。然后把这些幅度映射到一个灰度级表示,255 表示黑, 0 表示白色。幅度值越
大,相应的区域越黑。这样我们会得到一个随着时间变化的频谱图,这个就是描述语音信号的 spectrogram 声谱图。
音素(Phones)的属性可以更好的在声谱图里观察出来。另外,通过观察共振峰和它们的转变可以更好的识别声音。隐马尔科夫模型(Hidden Markov Models)就是隐含地对声谱图进行建模以达到好的识别性能。还有一个作用就是它可以直观的评估 TTS 系统(text to speech)的好坏,直接对比合成的语音和自然的语音声谱图的匹配度即可。上图是中文“区”这个字的时域和频域语音的频谱图。峰值就表示语音的主要频率成分,这些峰值称为共振峰(formants),而共振峰就是携带了声音的辨识属性。用它就可以识别不同的声音。
要提取的不仅仅是共振峰的位置,还得提取它们转变的过程。所以提取的是频谱的包络(Spectral Envelope)。这包络就是一条连接这些共振峰点的平滑曲线。
###Mel 频率分析(Mel-Frequency Analysis)
给一段语音,可以得到了它的频谱包络(连接所有共振峰值点的平滑曲线)了。但是,对于人类听觉感知的实验表明,人类听觉的感知只聚焦在某些特定的区域,而不是整个频谱包络。
而 Mel 频率分析就是基于人类听觉感知实验的。实验观测发现人耳就像一个滤波器组一样,它只关注某些特定的频率分量(人的听觉对频率是有选择性的)。也就说,它只让某些频率的信号通过,而压根就直接无视它不想感知的某些频率信号。但是这些滤波器在频率坐标轴上却不是统一分布的,在低频区域有很多的滤波器,他们分布比较密集,但在高频区域,滤波器的数目就变得比较少,分布很稀疏。
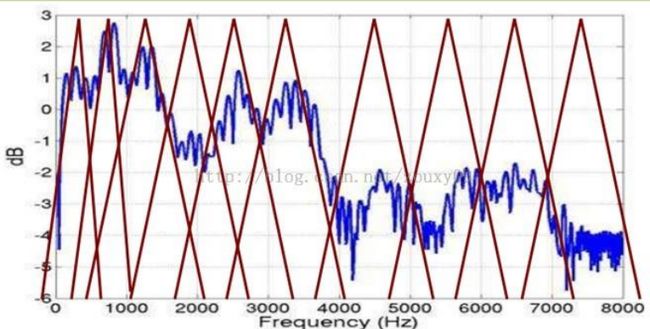
人的听觉系统是一个特殊的非线性系统,它响应不同频率信号的灵敏度是不同的。在语音特征的提取上,人类听觉系统做得非常好,它不仅能提取出语义信息, 而且能提取出说话人的个人特征,这些都是现有的语音识别系统所望尘莫及的。如果在语音识别系统中能模拟人类听觉感知处理特点,就有可能提高语音的识别率。
梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)考虑到了人类的听觉特征,先将线性频谱映射到基于听觉感知的 Mel 非线性频谱中,然后转换到倒谱上。
将普通频率转化到 Mel 频率的公式是:
m e l ( f ) = 2595 ∗ log 1 0 ( 1 + ( f / 700 ) = 1127 log [ 1 + f H z / 700 ] mel ( f ) = 2595*\log_10( 1 +( f / 700 )=1127\log[1+f_{Hz}/700] mel(f)=2595∗log10(1+(f/700)=1127log[1+fHz/700]
由下图可以看到,它可以将不统一的频率转化为统一的频率,也就是统一的滤波器组。
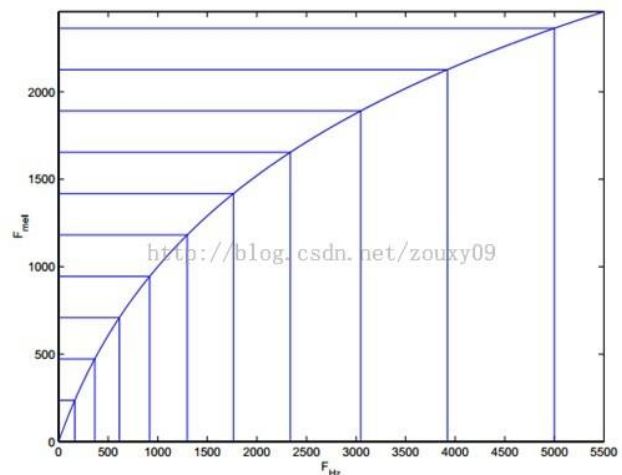
在 Mel 频域内,人对音调的感知度为线性关系。举例来说,如果两段语音的 Mel 频率相差两倍,则人耳听起来两者的音调也相差两倍。
###PLP(perceptual linear prediction)
PLP尽量模拟听觉的心里声学获得的系数,人类听觉的三个特性由PLP实现:
- 人耳对频率响应的非线性
- 耳蜗的临界频带
- 人耳对响度响应的非线性
首先非线性响应频率通过下式将频谱变换到 f b a r k f_{bark} fbarkBark频率范围获得。
f b a r k = log f H z 600 + [ ( f H z 600 ) 2 + 1 ] 0.5 (5.2) f_{bark}=\log{\frac{f_{Hz}}{600}+[(\frac{f_{Hz}}{600})^2+1]^{0.5}} \tag {5.2} fbark=log600fHz+[(600fHz)2+1]0.5(5.2)
上述获得的频谱然后和一系列和人耳心里声学相似的临界频率滤波器卷积。
人耳对3.5kHz较为敏感,这个可以通过一个频谱滤波器来模拟:
E ( ω ) = ( ω 2 + 56.8 × 1 0 6 ) ω 4 ( ω 2 + 6.3 × 1 0 6 ) 2 ( ω 2 + 0.38 × 1 0 9 ) ( ω 6 + 9.58 × 1 0 26 ) E(\omega)=\frac{(\omega^2+56.8×10^6)\omega^4}{(\omega^2+6.3×10^6)^2(\omega^2+0.38×10^9)(\omega^6+9.58×10^{26})} E(ω)=(ω2+6.3×106)2(ω2+0.38×109)(ω6+9.58×1026)(ω2+56.8×106)ω4
最后对响度频率取立方根,这个反映的就是观察到频率和感知到频率的非线性关系。
u ( n ) = α n 1 u n 1 ( n − 1 ) + α n 2 u n 2 ( n − 1 ) u(n)=\alpha_{n1}u_{n1}(n-1)+\alpha_{n2}u_{n2}(n-1) u(n)=αn1un1(n−1)+αn2un2(n−1)
二维高斯联合分布
p ( x , y ) = 1 2 π σ 1 σ 2 ( 1 − ρ 2 ) exp [ − 1 2 ( 1 − ρ 2 ) ( − ( x − μ 1 ) 2 σ 1 2 ) − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 ) 2 σ 2 2 ] p(x,y)=\frac{1}{2\pi \sigma_1 \sigma_2 \sqrt(1-\rho^2)}\exp [-\frac{1}{2(1-\rho^2)}(-\frac{(x-\mu_1)^2}{\sigma_1^2})-\frac{2\rho(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}] p(x,y)=2πσ1σ2(1−ρ2)1exp[−2(1−ρ2)1(−σ12(x−μ1)2)−σ1σ22ρ(x−μ1)(y−μ2)+σ22(y−μ2)2]
p ( x , y ) = p ( x ) ⋅ p ( y ) = exp [ − ( x − μ 1 ) 2 σ 1 2 ] ⋅ exp [ − ( x − μ 2 ) 2 σ 2 2 ] ≈ exp [ − ( x − μ 1 ) 2 σ 1 2 ] + exp [ − ( x − μ 2 ) 2 σ 2 2 ] p(x,y)=p(x) \cdot p(y)=\exp[-\frac{(x-\mu_1)^2}{\sigma_1^2}]\cdot \exp[-\frac{(x-\mu_2)^2}{\sigma_2^2}] \approx \exp[-\frac{(x-\mu_1)^2}{\sigma_1^2}]+ \exp[-\frac{(x-\mu_2)^2}{\sigma_2^2}] p(x,y)=p(x)⋅p(y)=exp[−σ12(x−μ1)2]⋅exp[−σ22(x−μ2)2]≈exp[−σ12(x−μ1)2]+exp[−σ22(x−μ2)2]
噪声均值更新:
u n j ( n ) = u n j ( n − 1 ) + [ 1 − F v a d ( n ) ] ⋅ K Δ n ⋅ ∇ u n j ⋅ p n ( x ( n ) ∣ H 0 ) p 0 ( x ( n ) ∣ H 0 ) + p 0 ( x ( n ) ∣ H 1 ) + K L [ x min ( n ) − u n ( n ) ] u_{nj}(n)={u_{nj}}(n-1)+[1-F_{vad}(n)]\cdot{K_{\Delta n}}\cdot \nabla_{u_{nj}}\cdot \frac{{p_n}({x(n)|H_0})}{{{p_0}({x(n)|H_0})}+{p_0}({x(n)|H_1})}+{K_L}[{{x_{\min}}(n)-{u_n}(n)}] unj(n)=unj(n−1)+[1−Fvad(n)]⋅KΔn⋅∇unj⋅p0(x(n)∣H0)+p0(x(n)∣H1)pn(x(n)∣H0)+KL[xmin(n)−un(n)]
语音模型均值更新:
u s j ( n ) = u s j ( n − 1 ) + F v a d ( n ) ⋅ K Δ s ⋅ ∇ u s j ⋅ p n ( x ( n ) ∣ H 1 ) p 0 ( x ∣ H 1 ) + p 0 ( x ∣ H 0 ) ; ∇ u s j = ( x − μ s j 2 σ s j 2 ) u_{sj}(n)={u_{sj}}(n-1)+F_{vad}(n)\cdot{K_{\Delta s}}\cdot \nabla_{{u_{sj}}} \cdot \frac{{p_n}({x(n)|H_1})} {{{p_0}({x|H_1})}+{p_0}({x|H_0})}; \nabla_{u_{sj}}=(\frac{x-\mu_{sj}}{2\sigma_{sj}^2}) usj(n)=usj(n−1)+Fvad(n)⋅KΔs⋅∇usj⋅p0(x∣H1)+p0(x∣H0)pn(x(n)∣H1);∇usj=(2σsj2x−μsj)
噪声模型方差跟新:
σ n j ( n ) = σ n j ( n − 1 ) + [ 1 − F v a d ( n ) ] ⋅ C Δ n ⋅ ∇ σ n j ⋅ p ( x ( n ) ∣ H 0 ) p 0 ( x ( n ) ∣ H 0 ) + p 0 ( x ( n ) ∣ H 1 ) {\sigma_{nj}}(n)=\sigma_{nj}(n-1)+[{1-{F_{vad}}(n)}]\cdot{C_{\Delta n}}\cdot \nabla_{\sigma_{nj}}\cdot\frac{{p}({x(n)|H_0})}{{{p_0}({x(n)|H_0})}+{{p_0}({x(n)|H_1})}} σnj(n)=σnj(n−1)+[1−Fvad(n)]⋅CΔn⋅∇σnj⋅p0(x(n)∣H0)+p0(x(n)∣H1)p(x(n)∣H0)
语音模型方差跟新
σ s j ( n ) = σ s j ( n − 1 ) + F v a d ( n ) ⋅ C Δ n ⋅ ∇ σ s j p ( x ( n ) ∣ H 1 ) p 0 ( x ( n ) ∣ H 0 ) + p 0 ( x ( n ) ∣ H 1 ) \sigma_{sj}(n)=\sigma_{sj}(n-1)+{F_{vad}}(n)\cdot{C_{\Delta n}}\cdot {\nabla_{\sigma_{sj}}} \frac{{p}({x(n)|H_1})}{{{p_0}({x(n)|H_0})}+{{p_0}({x(n)|H_1})}} σsj(n)=σsj(n−1)+Fvad(n)⋅CΔn⋅∇σsjp0(x(n)∣H0)+p0(x(n)∣H1)p(x(n)∣H1)