Python语音基础操作--3.1语音分帧与加窗

《语音信号处理试验教程》（梁瑞宇等）的代码主要是Matlab实现的，现在Python比较热门，所以把这个项目大部分内容写成了Python实现，大部分是手动写的。使用CSDN博客查看帮助文件：

Python语音基础操作–2.1语音录制，播放，读取
Python语音基础操作–2.2语音编辑
Python语音基础操作–2.3声强与响度
Python语音基础操作–2.4语音信号生成
Python语音基础操作–3.1语音分帧与加窗
Python语音基础操作–3.2短时时域分析
Python语音基础操作–3.3短时频域分析
Python语音基础操作–3.4倒谱分析与MFCC系数
Python语音基础操作–4.1语音端点检测
Python语音基础操作–4.2基音周期检测
Python语音基础操作–4.3共振峰估计
Python语音基础操作–5.1自适应滤波
Python语音基础操作–5.2谱减法
Python语音基础操作–5.4小波分解
Python语音基础操作–6.1PCM编码
Python语音基础操作–6.2LPC编码
Python语音基础操作–6.3ADPCM编码
Python语音基础操作–7.1帧合并
Python语音基础操作–7.2LPC的语音合成
Python语音基础操作–10.1基于动态时间规整(DTW)的孤立字语音识别试验
Python语音基础操作–10.2隐马尔科夫模型的孤立字识别
Python语音基础操作–11.1矢量量化(VQ)的说话人情感识别
Python语音基础操作–11.2基于GMM的说话人识别模型
Python语音基础操作–12.1基于KNN的情感识别
Python语音基础操作–12.2基于神经网络的情感识别
Python语音基础操作–12.3基于支持向量机SVM的语音情感识别
Python语音基础操作–12.4基于LDA，PCA的语音情感识别

代码可在Github上下载：busyyang/python_sound_open

一般来讲，语音信号的采样率是挺高的，而且认为语音信号在一定时间段的基本特性不会发生较大的变化，具有一定的短时平稳性。进行“短时分析”就行将信号分解成一段一段地来处理，每一段就叫一帧，大约10-30ms，也就是一秒钟大约33-100帧，对于通常10K的采样率来说，这样也能有一定的信息存在。分帧通常有一定的交叠部分，就是帧移。帧移与帧长的比通常为0~1/2。

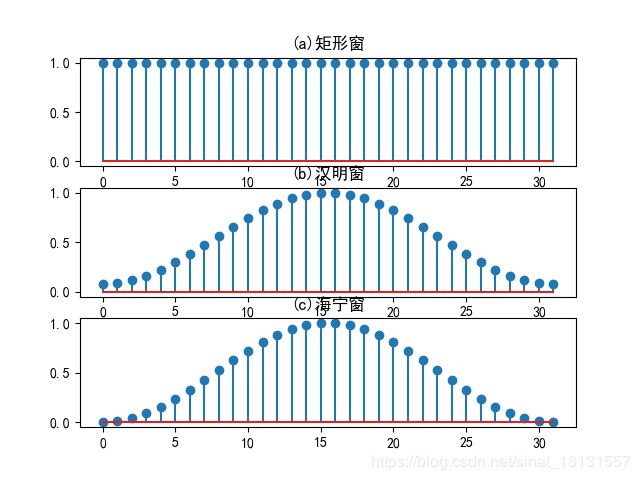
分帧就是通过加窗函数实现的，假设原始信号为$s(n)$，窗函数为$w(n)$，那么分帧就是$s_w(n)=s(n)\ast w(n)$，窗函数需要满足1. 窗口两端不引起急剧变化，应该平滑过渡到0，2.在频域有较宽的3dB贷款以及较大的边带最大值。窗口的长度一般为10~20ms。有三种常见的窗函数为：

• 矩形窗
  $$w(n)=\{\begin{array}{ll}1& ,0⩽n⩽N-1\\ 0& ,others\end{array}\text{\hspace{1em}(矩形窗)}$$

• 汉明窗

$$w(n)=\{\begin{array}{ll}0.54-0.46\cos [2\pi n/(N-1)]& ,0⩽n⩽N-1\\ 0& ,others\end{array}\text{\hspace{1em}(汉明窗)}$$

• 海宁窗

$$w(n)=\{\begin{array}{ll}0.5(1-\cos (2\pi n/(N-1)))& ,0⩽n⩽N-1\\ 0& ,others\end{array}\text{\hspace{1em}(汉明窗)}$$

其图形如下：

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

N = 32
nn = [i for i in range(N)]
plt.subplot(3, 1, 1)
plt.stem(np.ones(N))
plt.title('(a)矩形窗')

w = 0.54 - 0.46 * np.cos(np.multiply(nn, 2 * np.pi) / (N - 1))
plt.subplot(3, 1, 2)
plt.stem(w)
plt.title('(b)汉明窗')

w = 0.5 * (1 - np.cos(np.multiply(nn, 2 * np.pi) / (N - 1)))
plt.subplot(3, 1, 3)
plt.stem(w)
plt.title('(c)海宁窗')
# plt.show()
plt.savefig('images/window.png')
plt.close()

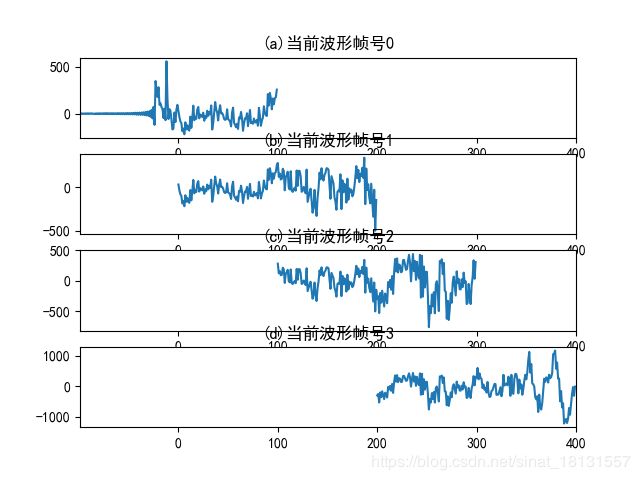
分帧操作，相当于将信号分解为若干个信号片段，并将片段与窗函数进行对应元素的乘法。

from scipy.io import wavfile
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


def enframe(x, win, inc=None):
    nx = len(x)
    if isinstance(win, list):
        nwin = len(win)
        nlen = nwin  # 帧长=窗长
    elif isinstance(win, int):
        nwin = 1
        nlen = win  # 设置为帧长
    if inc is None:
        inc = nlen
    nf = (nx - nlen + inc) // inc
    frameout = np.zeros((nf, nlen))
    indf = np.multiply(inc, np.array([i for i in range(nf)]))
    for i in range(nf):
        frameout[i, :] = x[indf[i]:indf[i] + nlen]
    if isinstance(win, list):
        frameout = np.multiply(frameout, np.array(win))
    return frameout


fs, data = wavfile.read('C3_1_y.wav')
inc = 100
wlen = 200
en = enframe(data, wlen, inc)
i = input('起始帧(i):')
i = int(i)
tlabel = i
plt.subplot(4, 1, 1)
x = [i for i in range((tlabel - 1) * inc, (tlabel - 1) * inc + wlen)]
plt.plot(x, en[tlabel, :])
plt.xlim([(i - 1) * inc + 1, (i + 2) * inc + wlen])
plt.title('(a)当前波形帧号{}'.format(tlabel))

plt.subplot(4, 1, 2)
x = [i for i in range((tlabel + 1 - 1) * inc, (tlabel + 1 - 1) * inc + wlen)]
plt.plot(x, en[i + 1, :])
plt.xlim([(i - 1) * inc + 1, (i + 2) * inc + wlen])
plt.title('(b)当前波形帧号{}'.format(tlabel + 1))

plt.subplot(4, 1, 3)
x = [i for i in range((tlabel + 2 - 1) * inc, (tlabel + 2 - 1) * inc + wlen)]
plt.plot(x, en[i + 2, :])
plt.xlim([(i - 1) * inc + 1, (i + 2) * inc + wlen])
plt.title('(c)当前波形帧号{}'.format(tlabel + 2))

plt.subplot(4, 1, 4)
x = [i for i in range((tlabel + 3 - 1) * inc, (tlabel + 3 - 1) * inc + wlen)]
plt.plot(x, en[i + 3, :])
plt.xlim([(i - 1) * inc + 1, (i + 2) * inc + wlen])
plt.title('(d)当前波形帧号{}'.format(tlabel + 3))

# plt.show()
plt.savefig('images/en.png')
plt.close()

另外，也可以直接使用numpy.hanning(N)来获得窗函数。其中N就是点数。