three.js 三维室内地图导航实例

总用three.js做一些零散好玩的效果，却也没怎么把他们整合到一起，最近因一位网友需要，把室内地图导航走通了一下。

这里主要在前端使用了有名的Dijkstra算法，关于此算法这里不再赘述，这里描述一下从路径数据准备到最佳路径输出的整个过程。

在线体验地址

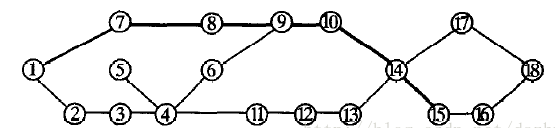
1.节点数据准备

节点是路径生成的基础，我们需要在建筑的基础上，拾取出场景中所有路径节点的坐标，作为基础数据并保存。

节点数据示例：

/**
 * 保存所有节点以及名称，也可包含其他信息
 * */
var points = {
    0:{name:"节点0",position:[-10.89,0.6,-21.11]},
    1:{name:"节点1",position:[1.45,0.6,-21.47]},
    2:{name:"节点2",position:[1.39,0.6,-15.38]},
    3:{name:"节点3",position:[11.59,0.6,-15.25]},
    4:{name:"节点4",position:[0.92,0.6,-25.03]},
    5:{name:"节点5",position:[10.88,0.6,-24.98]},
    6:{name:"节点6",position:[17.68,0.6,-14.62]},
    7:{name:"节点7",position:[14.11,0.6,-9.71]},
    8:{name:"节点8",position:[24.87,0.6,-18.04]},
    9:{name:"节点9",position:[30.06,0.6,-25.16]},
    10:{name:"节点10",position:[25.47,0.6,-35.77]},
    11:{name:"节点11",position:[19.44,0.6,-37.08]},
    12:{name:"节点12",position:[37.24,0.6,-22.84]},
    13:{name:"节点13",position:[15.98,0.6,-48.0]},
    14:{name:"节点14",position:[11.80,0.6,-33.81]},
    15:{name:"节点15",position:[2.06,0.6,-33.94]},
    16:{name:"节点16",position:[2.63,0.6,-41.60]},
    17:{name:"节点17",position:[-13.52,0.6,-40.64]},
    18:{name:"节点18",position:[-29.23,0.6,-40.49]},
    19:{name:"节点19",position:[-11.59,0.6,-56.85]}
}

2.路径数据准备

路径是表示节点与节点之间的连通性以及距离，这个距离也可以替换为路径已知的其他因素消耗。路径数据中，如果不需要区分道路的方向，那么节点1和节点2之间只需要1条路径数据；反之如果需要区分，那么节点1到节点2为1条路径数据，节点2到节点1也是一条路径数据。

路径数据示例：

/**
 *  此项为所有节点的连通性，这里测试数据中区分了道路的双向
 *  如果线路不区分双向，则同一条道路的两个方向数据可以合并为一条，比如{src:0,des:1}与{src:1,des:0}可合并为{src:0,des:1}
 * */
var routes = [
    {src:0,des:1,cost:12.345,extra:"0-1"},
    {src:1,des:0,cost:12.345,extra:"1-0"},
    {src:0,des:17,cost:19.706,extra:"0-17"},
    {src:17,des:0,cost:19.706,extra:"17-0"},
    {src:1,des:2,cost:6.090,extra:"1-2"},
    {src:2,des:1,cost:6.090,extra:"2-1"},
    {src:1,des:4,cost:3.599,extra:"1-4"},
    {src:4,des:1,cost:3.599,extra:"4-1"},
    {src:2,des:3,cost:10.201,extra:"2-3"},
    {src:3,des:2,cost:10.201,extra:"3-2"},
    {src:3,des:5,cost:9.756,extra:"3-5"},
    {src:5,des:3,cost:9.756,extra:"5-3"},
    {src:3,des:6,cost:6.122,extra:"3-6"},
    {src:6,des:3,cost:6.122,extra:"6-3"},
    {src:4,des:5,cost:9.960,extra:"4-5"},
    {src:5,des:4,cost:9.960,extra:"5-4"},
    {src:4,des:15,cost:8.983,extra:"4-15"},
    {src:15,des:4,cost:8.983,extra:"15-4"},
    {src:5,des:14,cost:8.878,extra:"5-14"},
    {src:14,des:5,cost:8.878,extra:"14-5"},
    {src:6,des:7,cost:6.071,extra:"6-7"},
    {src:7,des:6,cost:6.071,extra:"7-6"},
    {src:6,des:8,cost:7.962,extra:"6-8"},
    {src:8,des:6,cost:7.962,extra:"8-6"},
    {src:8,des:9,cost:8.811,extra:"8-9"},
    {src:9,des:8,cost:8.811,extra:"9-8"},
    {src:9,des:10,cost:11.560,extra:"9-10"},
    {src:10,des:9,cost:11.560,extra:"10-9"},
    {src:9,des:12,cost:7.546,extra:"9-12"},
    {src:12,des:9,cost:7.546,extra:"12-9"},
    {src:10,des:11,cost:6.171,extra:"10-11"},
    {src:11,des:10,cost:6.171,extra:"11-10"},
    {src:11,des:13,cost:11.455,extra:"11-13"},
    {src:13,des:11,cost:11.455,extra:"13-11"},
    {src:11,des:14,cost:8.310,extra:"11-14"},
    {src:14,des:11,cost:8.310,extra:"14-11"},
    {src:14,des:15,cost:9.741,extra:"14-15"},
    {src:15,des:14,cost:9.741,extra:"15-14"},
    {src:15,des:16,cost:7.681,extra:"15-16"},
    {src:16,des:15,cost:7.681,extra:"16-15"},
    {src:15,des:17,cost:16.960,extra:"15-17"},
    {src:17,des:15,cost:16.960,extra:"17-15"},
    {src:17,des:18,cost:15.711,extra:"17-18"},
    {src:18,des:17,cost:15.711,extra:"18-17"},
    {src:17,des:19,cost:16.324,extra:"17-19"},
    {src:19,des:17,cost:16.324,extra:"19-17"}
]

3.最佳路径选择

3.1 初始化邻接矩阵

邻接矩阵表示节点和节点之间连接以及消耗，为行列均为总节点数的矩阵，默认值均为Infinity表示无法到达，根据节点基础数据和路径基础数据对邻接矩阵进行填充，填充出能直接到达的矩阵行列。

3.2 寻找最佳路径

使用Dijkstra算法，计算出起始节点到其他所有节点的长度，返回起始节点到其他所有节点的路线消耗（距离）数组以及经过的节点数组。

/**
 * @param {Array} adjMatrix 邻接矩阵
 * @param {number} sourceV 源点的索引
 */
function Dijkstra(adjMatrix,sourceV) {
    ...
    return {
        path: path,
        dist: dist
    };
}

4.路径输出

根据路径经过的节点，找出全部的路径，并打印出所有的路径信息。

/**
 * @param {number} v 起点索引
 * @param {number} d 终点索引
 * @param {Array} adjMatrix 邻接矩阵
 */
function searchPath(v, d, adjMatrix) {
    ...
    return {distance:dist[d],path:rarr}
}

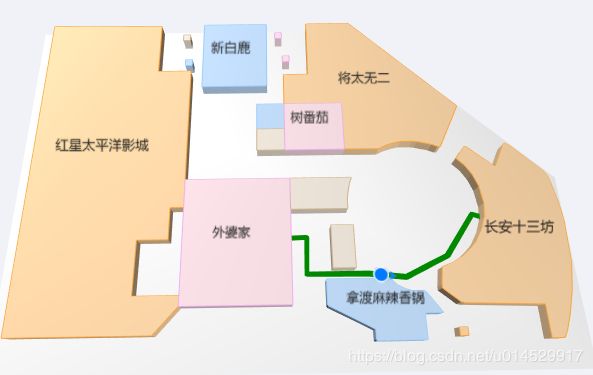
5.效果图