机器学习——回归问题(2020最新版)

一、回归的由来

 

 

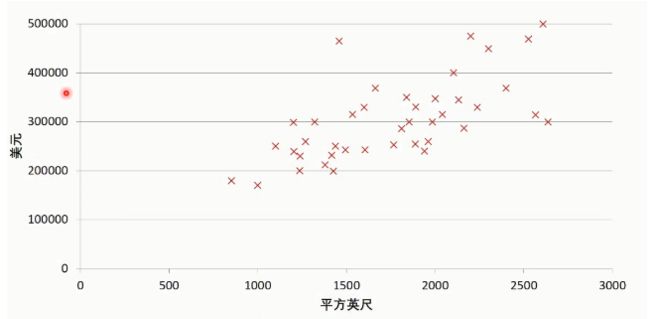
二、房价预测问题

 

 

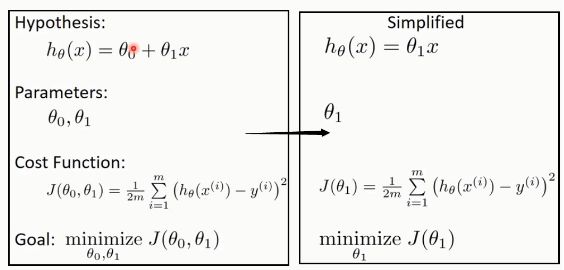
三、一元线性回归定义

 

 

四、代价函数(cost func)/损失函数(loss func)

(1) 为什么要使用平方？因为如果使用绝对值来计算误差，不方便计算；平方更准确的计算和衡量。

(2) 代价函数最小，该回归线的拟合效果越好。

(3) 为什么要乘一个1/2? 为了求解的时候更加方便更加好看，其实可以不用乘；比如对该函数求导时，可以和平方的2抵消。

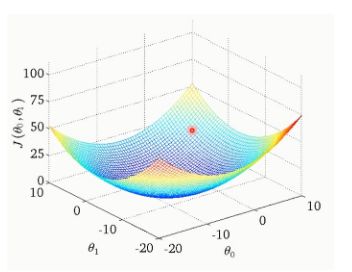
(4) 每一个@1对于一个代价函数值，这里可以看出当@1取1时，代价函数最小。即确定出@1、@0的值了。

(5) 最里面的等高线，代价函数的值最小。

 

 

五、相关系数

(1) 左图点的分布更加接近直线，相关系数更高。

(2) 当相关系数大于零，正相关；当相关系数小于零，负相关。

 

 

六、决定系数

(1) 决定系数越接近1，说明他们之间的关系越接近于线性关系；越接近于0，说明他们之间的关系越不接近于线性关系。

 

 

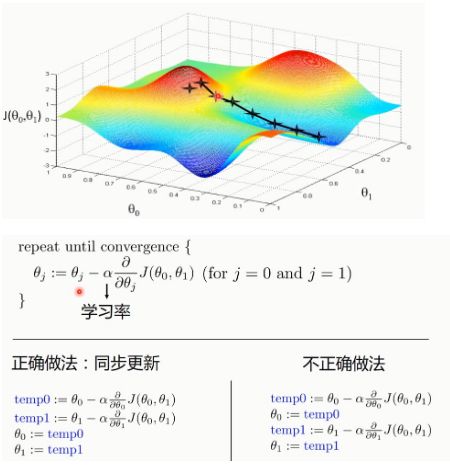
七、梯度下降法

7.1 梯度下降法优化过程

如果是二维的话，同时更新@1和@0，来进行梯度下降。

如果是一维的，也是不断通过梯度下降来改变@1的值从而再来进行梯度下降

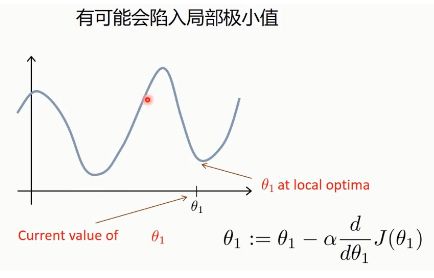
(1) 关于学习率，需要一定的经验来选择，不是固定的，且在0~1之间。

(2) 同样有可能陷入局部最小值(at local optima)。

使用梯度下降法来求解线性回归：

以@0为例，对@0求导：

同样对@1进行求导，多了一个x：

相应结果：

此外，线性回归的代价函数是凸函数

因为使用梯度下降法，总会找到全局最小值(都能走到最低点，即凸函数)

(3) 所以对于，这种非凸函数，只能找到局部极小值，所以无法使用梯度下降法进行优化。

 

7.2 使用梯度下降法完成一元线性回归(python)

import numpy as np
import matplotlib.pyplot as plt

"""
@desc 使用data.csv数据+梯度下降法进行一元线性回归
"""
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)

# 学习率(learning rate)
lr = 0.0001
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 50


# 最小二乘法（计算cost func）
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2


# 梯度下降法
def gradient_descent_method(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(0, len(x_data)):
        b_grad = 0
        k_grad = 0
        # 先求平均再求和
        for j in range(0, len(x_data)):
            b_grad += (1 / m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1 / m) * (((k * x_data[j]) + b) - y_data[j]) * x_data[j]
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)

        # 每次迭代5次，输出一次图像,可以更好的看清这个梯度下降的优化过程
        # if i % 5 == 0:
        #     print("epochs:", i)
        #     plt.plot(x_data, y_data, "b.")
        #     plt.plot(x_data, k * x_data + b, "r")
        #     plt.show()
    return b, k


print("Starting b={0}, k={1}, error={2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_method(x_data, y_data, b, k, lr, epochs)
print("After {0}, iterations b={1}, k={2}, error={3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

#画图
#b. b表示blue，颜色是blue;.表示用点的形式画出来，也叫散点图
plt.plot(x_data, y_data, "b.")
#默认是线图，红色
plt.plot(x_data, k*x_data+b, "r")
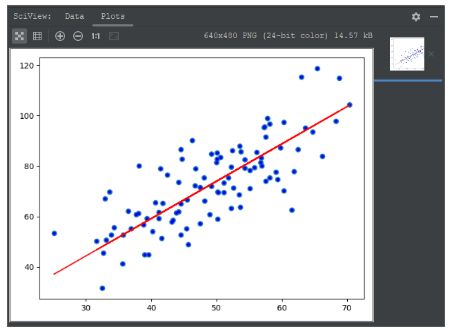
plt.show()

最终的优化效果如下：

 

7.3 使用sklearn进行一元线性回归(python)

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

#载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)
# plt.show()
# print(x_data.shape)

x_data = data[:, 0, np.newaxis]
#当使用np.newaxis加一维，变成二维数组后，这里的x_data相当于1行， 100列的二维数组；
#之所以要这么做，是因为后面fit函数要求数据类型是这样
y_data = data[:, 1, np.newaxis]
#创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)

#画图
plt.plot(x_data, y_data, "b.")
plt.plot(x_data, model.predict(x_data), "r")
plt.show()

最终的优化效果如下(比上面效果可能还好一些),使用封装包更加简单：

 

 

八、矩阵

 

 

九、多元线性回归

9.1 多元线性回归定义

比如不仅仅只使用房子的面积来判断房子的价格，而使用多个特征：

9.2 快递送货的实战

9.2.1 使用梯度下降法实现多元线性回归(python)

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    gradient_descent_method
  Author:      newlinfeng
  Date:        2020/7/22 0022  11:23
  Description: 使用Delivery.csv数据+梯度下降法进行多元线性回归
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 读入数据
data = genfromtxt(r"Delivery.csv", delimiter=",")
print(data)

# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
print(x_data)
print(y_data)

# 学习率learning rate
lr = 0.0001
# 参数
theta0 = 0
theta1 = 0
theta2 = 0
# 最大迭代次数
epochs = 1000


# 最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (theta1 * x_data[i, 0] + theta2 * x_data[i, 1] + theta0)) ** 2
    return totalError / float(len(x_data))

#cost func
def gradient_descent_runner(x_data, y_data, theta1, theta2, theta0, lr, epochs):
    # 计算总量数据
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        theta0_grad = 0
        theta1_grad = 0
        theta2_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            theta0_grad += -(1 / m) * (y_data[j] - (theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0))
            theta1_grad += -(1 / m) * (y_data[j] - (theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0)) * x_data[
                j, 0]
            theta2_grad += -(1 / m) * (y_data[j] - (theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0)) * x_data[
                j, 1]
        #更新theta0,theta1,theta2
        theta0 -= lr*theta0_grad
        theta1 -= lr*theta1_grad
        theta2 -= lr*theta2_grad

    return theta0, theta1, theta2

print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}"
      .format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta1, theta2, theta0, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".format(
    epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)
))

#3D图展示
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c = 'r', marker = 'o', s = 100)
x0 = x_data[:, 0]
x1 = x_data[:, 1]
#生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + theta1*x0+theta2*x1
#画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel("Mills")
ax.set_ylabel("Num of Deliveries")
ax.set_zlabel("Time")
#显示图像
plt.show()

最终拟合的结果如下：

 

9.2.2 使用梯度下降法实现多元线性回归(python)

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    sklearn_method_mult
  Author:      newlinfeng
  Date:        2020/7/22 0022  15:04
  Description: 使用Delivery.csv数据+sklearn法进行多元线性回归
-------------------------------------------------------------------------------
"""

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#读入数据
data = np.genfromtxt("Delivery.csv", delimiter=",")
print(data)

#切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
print(x_data)
print(y_data)

#创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)

#系数
print("coefficients:", model.coef_)
#截距
print("intercept:", model.intercept_)
#测试
x_test = [[102, 4]]
predict = model.predict(x_test)
print("predict:", predict)

#3D图展示
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c = 'r', marker = 'o', s = 100)
x0 = x_data[:, 0]
x1 = x_data[:, 1]
#生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + model.coef_[0]*x0+model.coef_[1]*x1
#画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel("Mills")
ax.set_ylabel("Num of Deliveries")
ax.set_zlabel("Time")
#显示图像
plt.show()

最终拟合的结果如下，效果和梯度下降类似：

 

 

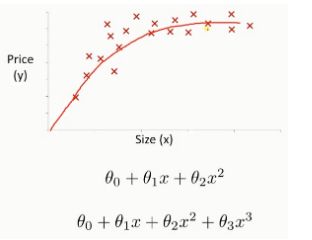
九、多项式回归

 

 

十、标准方程法(直接求解出这个cost func的最小值，之前的梯度下降是使用一种不断逼近的方法来找到最小值)

(1) 标准方程法是解决线性回归的另一种方法(上面提到是都是梯度下降法)；

例如，同样是房子的价格和面积、卧室数量、层数、已使用年数等数据的关系，如下表：

X：样本的特征    w：权值参数，类似上面的a,b    y：结果：

10.1 这里还有两个概念：分子布局、分母布局

(1) 查询矩阵计算(求导方法)：https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities

其中：

然后再整理得到，即得出最后的w矩阵的值：

 

10.2 矩阵不可逆的情况

下面这两种情况，标准方程法无法使用：

 

 

十一、梯度下降法 VS 标准方程法

(1) sklearn使用的是标准方程法进行的封装，而不是梯度下降法

11.1 使用标准方程法实现一元线性回归

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    sem_univariate_method
  Author:      newlinfeng
  Date:        2020/7/22 0022  23:04
  Description: 使用标准方程法来进行一元线性回归
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt

#载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, 0, np.newaxis]
y_data = data[:, 1, np.newaxis]
plt.scatter(x_data, y_data)
plt.show()

print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
#给样本添加偏执项
X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)
print(X_data.shape)

print(X_data[:3])

#标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T*xMat #矩阵乘法, .T是转置矩阵的意思
    #计算矩阵对应的行列式的值，如果值为0，说明该矩阵没有逆矩阵
    if np.linalg.det(xTx) == 0.0:
        print("This matrix cannot do inverse")
        return
    # xTx,T为XTx的可逆矩阵
    ws = xTx.I*xMat.T*yMat
    return ws


ws = weights(X_data, y_data)
print(ws)


#画图
x_test = np.array([[20], [80]])
y_test = ws[0] +x_test*ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()

 

 

十二、特征缩放、交叉验证法

12.1 特征缩放

由于特征的不太一致，使用梯度下降法花费时间长，所以要进行预处理

 

12.2 进行预处理的方式有两种：数据归一化、均值标准化

方法1：数据归一化

方法2：均值标准化

 

12.3 交叉验证法

当数据量很小的时候可以采用这种方式，使用每个部分都作为测试集，其余作为验证集，再求平均得到相应的结果。

 

 

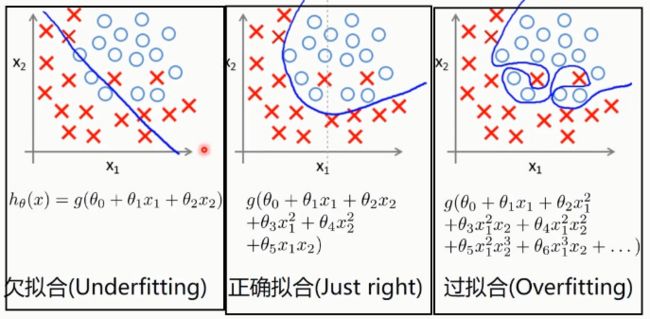
十三、过拟合(Overfitting)、正则化(Regularized)

13.1 过拟合(Overfitting)

回归的情况：

分类的情况：

防止过拟合的方式：

• 减少特征（有些特征可能没有特别大的用处或者直接是噪声）
• 增加数据量
• 正则化(Regularized)

 

13.2 正则化(Regularized)

 

 

十四、岭回归(Ridge Regression)

下面是岭回归的代价函数：

 

14.1 使用python实现岭回归

使用的数据集：Longley数据集：

使用sklearn实现岭回归：

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    rid_sklearn_method
  Author:      newlinfeng
  Date:        2020/7/26 0026  11:28
  Description: 使用sklearn算法实现岭回归
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt

#读入数据
data = genfromtxt(r"longley.csv", delimiter=",")

#切分数据
x_data = data[1:, 2:]
y_data = data[1:, 1]

#创建模型
#生成50个值
alphas_to_test = np.linspace(0.001, 1)
#创建模型，保存误差值
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
model.fit(x_data, y_data)

#岭系数
print(model.alpha_)
#loss值
print(model.cv_values_.shape)

#画图
#岭系数跟loss值的关系
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
#选取的岭系数值的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)), "ro")
plt.show()

model.predict(x_data[2, np.newaxis])

 

使用方程法实现岭回归：

使用该公式求解：

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    rid_standard_equation_method
  Author:      newlinfeng
  Date:        2020/7/27 0027  17:15
  Description: 使用标准方程法实现岭回归
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt

# 读入数据
data = genfromtxt(r"longley.csv", delimiter=",")

# 切分数据
x_data = data[1:, 2:]
y_data = data[1:, 1, np.newaxis]

# 给样本x_data添加一行偏置值
X_data = np.concatenate((np.ones((16, 1)), x_data), axis=1)


# 标准方程法求解回归系数
def weights(xArr, yArr, lam=0.2):
    x_Mat = np.mat(xArr)
    y_Mat = np.mat(yArr)
    xTx = x_Mat.T * x_Mat
    # eye()：用来生成单位矩阵，传入i的化就生成i*i的单位矩阵，这个shape[1]的值是7
    # 为什么是7？ 因为xTx是7*7列
    rxTx = xTx + np.eye(x_Mat.shape[1]) * lam
    # 计算矩阵的值，如果值为0，说明该矩阵没有逆矩阵
    if np.linalg.det(rxTx) == 0.0:
        print("This matrix cannot do inverse")
        return
    # xTx.I为xTx的逆矩阵
    ws = rxTx.I * x_Mat.T * y_Mat
    return ws

ws = weights(X_data, y_data)

#计算预测值
results = np.mat(X_data)*np.mat(ws)
print(results)

最终得到的预测结果与实际的结果差别很小：

 

 

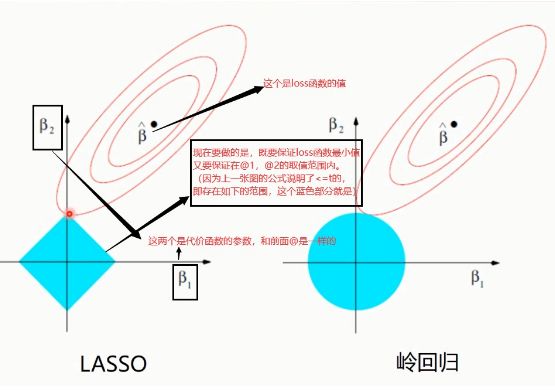
15.LASSO(The Least Absolute Shrinkage and Selectionator operator)

Lasso:最小绝对收缩与选择算子：

(1) 这里就很明显的看出，岭回归使用的是L2正则化，LASSO使用的是L1正则化。

(2) 由上图可以看出，Lasso很容易使得某个参数取值为0(左图@1就已经取值为0了)，而岭回归则很难。

15.1 使用python实现Lasso回归

使用sklearn实现LASSO回归：

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    las_sklearn_mathod
  Author:      newlinfeng
  Date:        2020/7/27 0027  22:21
  Description: 使用sklearn实现LASSO回归
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

#读入数据
data = genfromtxt(r"longley.csv", delimiter=",")

#切分数据
x_data = data[1:, 2:]
y_data = data[1:, 1]

#创建模型
model = linear_model.LassoCV()
model.fit(x_data, y_data)

#LASSON系数
print(model.alpha_)
#系数
print(model.coef_)

model.predict(x_data[-2, np.newaxis])

 

 

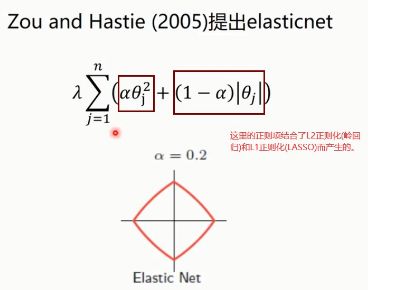
十六、弹性网(Elastic Net)

(1) 所以从该公式出发，既然集合了岭回归和LASSO，那么应该表现出更好的效果。

使用sklearn实现弹性网络：

# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
  FileName:    elas_sklearn_method
  Author:      newlinfeng
  Date:        2020/7/27 0027  22:55
  Description: 使用sklearn实现elastic net（弹性网络）
-------------------------------------------------------------------------------
"""
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

#读入数据
data = genfromtxt(r"longley.csv", delimiter=",")

#切分数据
x_data = data[1:, 2:]
y_data = data[1:, 1]

#创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data, y_data)

#elastic net系数
print(model.alpha_)
#每个特征系数
print(model.coef_)

#取x_data的-2行数据进行预测
model.predict(x_data[-2, np.newaxis])

 

 

到这里回归问题基本结束，接下来的逻辑回归实际上属于分类问题。

2020-07-28更新