Apollo学习笔记(8)车辆动力学模型
车辆动力学模型
动力学主要研究作用于物体的力与物体运动的关系,车辆动力学模型一般用于分析车辆的平顺性和车辆操纵的稳定性。对于车来说,研究车辆动力学,主要是研究车辆轮胎及其相关部件的受力情况。
正常情况下,车辆上的作用力沿着三个不同的轴分布:
-
纵轴上的力包括驱动力和制动力,以及滚动阻力和拖拽阻力作滚摆运动(roll);
-
横轴上的力包括转向力、离心力和侧风力,汽车绕横轴作俯仰运动(pitch);
-
立轴上的力包括车辆上下振荡施加的力,汽车绕立轴作偏摆或转向运动(yaw);
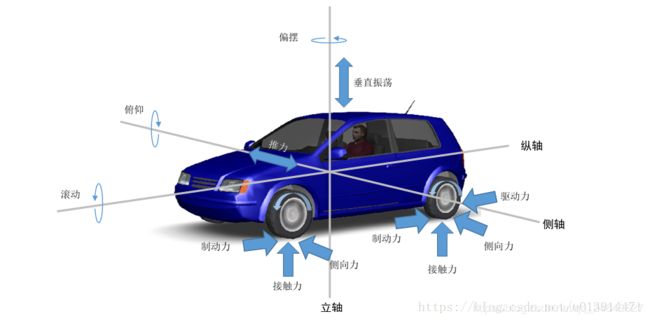
图 1 车 辆 受 力 模 型 图 1 \space车辆受力模型 图1 车辆受力模型
而在单车模型假设的前提下,再作如下假设1即可简单搭建车辆的动力学模型:
- 只考虑纯侧偏轮胎特性,忽略轮胎力的纵横向耦合关系;
- 用单车模型来描述车辆的运动,不考虑载荷的左右转移;
- 忽略横纵向空气动力学。
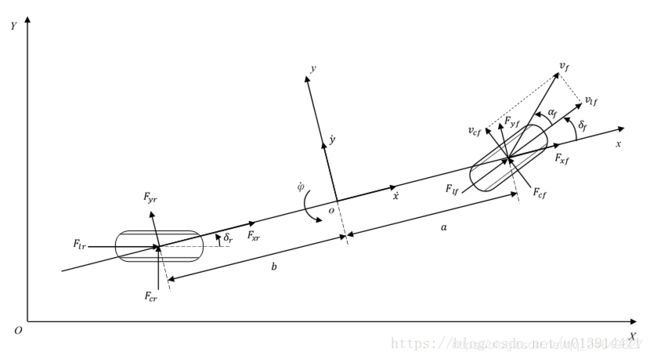
图 2 车 辆 单 车 模 型 受 力 状 态 图 2 \space车辆单车模型受力状态 图2 车辆单车模型受力状态
如图2所示, o x y z oxyz oxyz为固定于车身的车辆坐标系, O X Y OXY OXY为固定于地面的惯性坐标系。单车模型的车辆具有2个自由度:绕 z z z轴的横摆运动,和沿 x x x轴的纵向运动。
纵向指沿物体前进方向,横向(或侧向)指垂直纵向方向。
横向运动:出自横向的风力,以及曲线行驶时的离心力等。
纵向运动:受总驱动阻力、加速、减速等的影响。总驱动阻力由滚动阻力、拖拽阻力和坡度阻力等构成。
滑移角(slip−angle)(slip−angle):轮胎方向和轮胎速度方向的夹角。滑移角的产生主要是由于车轮所受合力方向并非朝向车轮行进方向,但车轮的偏移角通常较小。
图2中各符号定义:
| 符号 | 定义 |
|---|---|
| F l f , F l r F_{lf},F_{lr} Flf,Flr | 前、后轮胎受到的纵向力 |
| F c f , F c r F_{cf},F_{cr} Fcf,Fcr | 前、后轮胎受到的侧向力 |
| F x f , F x r F_{xf},F_{xr} Fxf,Fxr | 前、后轮胎受到的x方向力 |
| F y f , F y r F_{yf},F_{yr} Fyf,Fyr | 前、后轮胎受到的y方向力 |
| a, ℓ f \ell_f ℓf | 前悬长度 |
| b, ℓ r \ell_r ℓr | 后悬长度 |
| δ f \delta_f δf, δ \delta δ | 前轮偏角 |
| δ r \delta_r δr | 后轮偏角 |
| a f a_f af | 前轮偏移角 |
分别沿着 x x x, y y y, z z z轴做相关分析:
在x轴上:
m a x = F x f + F x r (1) ma_x=F_{xf}+F_{xr} \tag{1} max=Fxf+Fxr(1)
在y轴上:
m a y = F y f + F y r (2) ma_y=F_{yf}+F_{yr} \tag{2} may=Fyf+Fyr(2)
在z轴上:
I z φ ¨ = a F y f − b F y r (3) I_z\ddot{\varphi}=aF_{yf}-bF_{yr} \tag{3} Izφ¨=aFyf−bFyr(3)
式中,m为车辆质量, φ \varphi φ为车辆航向(yaw), I z I_z Iz为车辆绕z轴的转动惯量。
x轴方向的运动暂时不用考虑,车子翻滚不属于正常行驶范围。
横向动力学
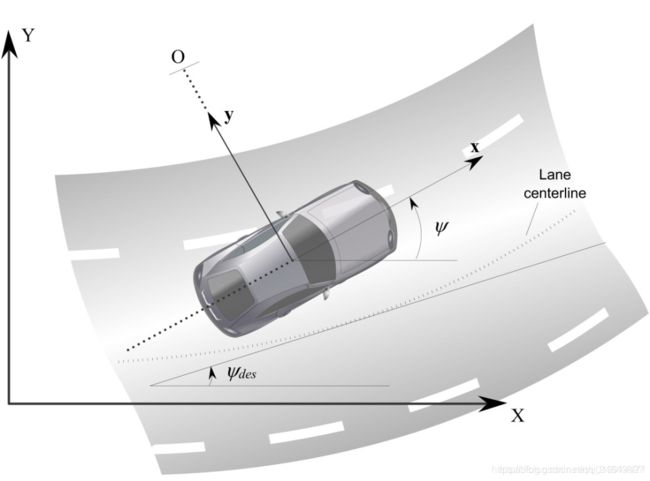
图 3 横 向 动 力 学 图\space 3 \space横向动力学 图 3 横向动力学
y轴方向加速度 a y a_y ay由两部分构成:沿着y轴方向的加速度 y ¨ \ddot{y} y¨,垂直于y轴方向的向心加速度 V x φ ˙ V_x\dot{\varphi} Vxφ˙
a y = y ¨ + V x φ ˙ a_y=\ddot{y}+V_x\dot{\varphi} ay=y¨+Vxφ˙
则式(2)可变为:
m ( y ¨ + V x φ ˙ ) = F y f + F y r (4) m(\ddot{y}+V_x\dot{\varphi})=F_{yf}+F_{yr} \tag{4} m(y¨+Vxφ˙)=Fyf+Fyr(4)
由于轮胎受到的横向压力,轮胎会有一个很小的滑移角,如图4所示
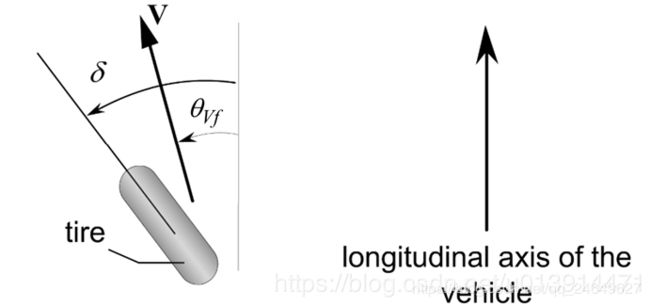
图 4 轮 胎 滑 移 角 图\space4 \space 轮胎滑移角 图 4 轮胎滑移角
前轮滑移角
a f = δ − θ V f (5) a_f=\delta-\theta_{Vf} \tag{5} af=δ−θVf(5)
其中, θ V f \theta_{Vf} θVf为前轮速度方向, δ \delta δ为前轮转角。
后轮滑移角
a r = − θ V r (6) a_r=-\theta_{Vr} \tag{6} ar=−θVr(6)
其中, θ V r \theta_{Vr} θVr为前轮速度方向。
则前轮所受到的横向力为
F y f = 2 C a f ( δ − θ V f ) (7) F_{yf}=2C_{af}(\delta-\theta_{Vf}) \tag{7} Fyf=2Caf(δ−θVf)(7)
后轮所受到的横向力为
F y r = 2 C a r ( − θ V r ) (8) F_{yr}=2C_{ar}(-\theta_{Vr}) \tag{8} Fyr=2Car(−θVr)(8)
其中, C a f C_{af} Caf、 C a r C_{ar} Car分别为前后轮的侧偏刚度(cornering stiffness),由于车辆前后各两个轮,所以受力要乘以2。
结合图4,可以有
tan ( θ V f ) = y ˙ + a φ ˙ V x (9) \tan(\theta_{Vf})=\frac{\dot{y}+a\dot{\varphi}}{V_{x}} \tag{9} tan(θVf)=Vxy˙+aφ˙(9)
tan ( θ V r ) = y ˙ − b φ ˙ V x (10) \tan(\theta_{Vr})=\frac{\dot{y}-b\dot{\varphi}}{V_{x}} \tag{10} tan(θVr)=Vxy˙−bφ˙(10)
式(9),(10)可以近似转换为:
θ V f = y ˙ + a φ ˙ V x (11) \theta_{Vf}=\frac{\dot{y}+a\dot{\varphi}}{V_{x}} \tag{11} θVf=Vxy˙+aφ˙(11)
θ V r = y ˙ − b φ ˙ V x (12) \theta_{Vr}=\frac{\dot{y}-b\dot{\varphi}}{V_{x}} \tag{12} θVr=Vxy˙−bφ˙(12)
将式(5),(6),(11),(12)带入式(2),(3)可以得到车辆动力学模型
d d t [ y y ˙ φ φ ˙ ] = [ 0 1 0 0 0 − 2 C a f + 2 C a r m V x 0 − V x − 2 C a f ℓ f − 2 C a r ℓ r m V x 0 0 0 1 0 − 2 C a f ℓ f − 2 C a r ℓ r I z V x 0 − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] [ y y ˙ φ φ ˙ ] + [ 0 2 C a f m 0 2 C a f ℓ f I z ] δ (13) \frac{d}{dt}\begin{bmatrix} y \\ \dot{y} \\ \varphi \\ \dot{\varphi} \\ \end{bmatrix} = \begin{bmatrix} 0 && 1 && 0 && 0 \\ 0 && -\frac{2C_{af}+2C_{ar}}{mV_{x}} && 0 && -V_{x}- \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{mV_{x}} \\ 0 && 0 && 0 && 1 \\ 0 && -\frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{I_{z}V_{x}} && 0 && -\frac{2C_{af}\ell_{f}^{2}+2C_{ar}\ell_{r}^{2}}{I_{z}V_{x}} \end{bmatrix} \begin{bmatrix} y \\ \dot{y} \\ \varphi \\ \dot{\varphi} \\ \end{bmatrix}+\begin{bmatrix} 0 \\ \frac{2C_{af}}{m} \\ 0 \\ \frac{2C_{af}\ell_{f}}{I_{z}} \\ \end{bmatrix}\delta \tag{13} dtd⎣⎢⎢⎡yy˙φφ˙⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001−mVx2Caf+2Car0−IzVx2Cafℓf−2Carℓr00000−Vx−mVx2Cafℓf−2Carℓr1−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤⎣⎢⎢⎡yy˙φφ˙⎦⎥⎥⎤+⎣⎢⎢⎡0m2Caf0Iz2Cafℓf⎦⎥⎥⎤δ(13)
式中, ℓ f \ell_{f} ℓf, ℓ r \ell_{r} ℓr分别为车辆的前悬距离,后悬距离,也就是前文中的a,b。
方向盘控制模型
横向控制主要通过控制轮胎转角实现,而对于驾驶员来说,可直接操控的是方向盘角度,因此在搭建车辆动力学模型时,可以以相对于道路的方向和距离误差为状态变量的动力学模型。
如上文所述, e 1 e_1 e1为横向误差,车辆质心到规划轨迹最近投影点的距离, e 2 e_2 e2为航向误差,车辆纵向速度为 V x V_x Vx,车辆转弯半径为 R R R,结合上文有:
车辆转过期望角度所需角速度
φ ˙ = V x / R (14) \dot{\varphi}=V_{x}/R \tag{14} φ˙=Vx/R(14)
所需横向加速度
a y d e s = V x 2 / R = V x φ d e s (15) a_{ydes}=V_{x}^{2}/R=V_{x} \space \varphi_{des} \tag{15} aydes=Vx2/R=Vx φdes(15)
则横向加速度误差
e ¨ 1 = a y − a y d e s = ( y ¨ + V x φ ˙ ) − V x 2 R = y ¨ + V x ( φ ˙ − φ ˙ d e s ) (16) \ddot{e}_1=a_{y}-a_{ydes}=(\ddot{y}+V_{x}\dot{\varphi})-\frac{V_{x}^{2}}{R}=\ddot{y}+V_{x}(\dot{\varphi} - \dot{\varphi}_{des}) \tag{16} e¨1=ay−aydes=(y¨+Vxφ˙)−RVx2=y¨+Vx(φ˙−φ˙des)(16)
横向速度误差为
e ˙ 1 = V y − V y d e s = y ˙ + V x ( φ − φ d e s ) (17) \dot{e}_1=V_{y}-V_{ydes}=\dot{y}+V_{x}(\varphi - \varphi_{des}) \tag{17} e˙1=Vy−Vydes=y˙+Vx(φ−φdes)(17)
航向误差
e 2 = φ − φ d e s (18) e_2=\varphi - \varphi_{des} \tag{18} e2=φ−φdes(18)
将式(17),(18)带入式(3),(4)后,有
d d t [ e 1 e ˙ 1 e 2 e ˙ 2 ] = [ 0 1 0 0 0 − 2 C a f + 2 C a r m V x 2 C a f + 2 C a r m − 2 C a f ℓ f − 2 C a r ℓ r m V x 0 0 0 1 0 − 2 C a f ℓ f − 2 C a r ℓ r I z V x 2 C a f ℓ f − 2 C a r ℓ r I z − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] [ e 1 e ˙ 1 e 2 e ˙ 2 ] + [ 0 2 C a f m 0 2 C a f ℓ f I z ] δ + [ 0 − V x − 2 C a f ℓ f − 2 C a r ℓ r m V x 0 − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] φ ˙ d e s (19) \frac{d}{dt}\begin{bmatrix} e_1 \\ \dot{e}_1 \\ e_2 \\ \dot{e}_2 \\ \end{bmatrix} = \begin{bmatrix} 0 && 1 && 0 && 0 \\ 0 && -\frac{2C_{af}+2C_{ar}}{mV_{x}} && \frac{2C_{af}+2C_{ar}}{m} && - \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{mV_{x}} \\ 0 && 0 && 0 && 1 \\ 0 && -\frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{I_{z}V_{x}} && \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{I_{z}} && -\frac{2C_{af}\ell_{f}^{2}+2C_{ar}\ell_{r}^{2}}{I_{z}V_{x}} \end{bmatrix}\begin{bmatrix} e_1 \\ \dot{e}_1 \\ e_2 \\ \dot{e}_2 \\ \end{bmatrix} \\ +\begin{bmatrix} 0 \\ \frac{2C_{af}}{m} \\ 0 \\ \frac{2C_{af}\ell_{f}}{I_{z}} \\ \end{bmatrix}\delta+ \begin{bmatrix} 0 \\ -V_{x}- \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{mV_{x}} \\ 0 \\ -\frac{2C_{af}\ell_{f}^{2}+2C_{ar}\ell_{r}^{2}}{I_{z}V_{x}} \\ \end{bmatrix}\dot{\varphi}_{des} \tag{19} dtd⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤=⎣⎢⎢⎢⎡00001−mVx2Caf+2Car0−IzVx2Cafℓf−2Carℓr0m2Caf+2Car0Iz2Cafℓf−2Carℓr0−mVx2Cafℓf−2Carℓr1−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤⎣⎢⎢⎡e1e˙1e2e˙2⎦⎥⎥⎤+⎣⎢⎢⎡0m2Caf0Iz2Cafℓf⎦⎥⎥⎤δ+⎣⎢⎢⎢⎡0−Vx−mVx2Cafℓf−2Carℓr0−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤φ˙des(19)
综上,车辆动力学模型在Apollo中主要使用的为横向动力学模型,且有以下假设前提,
- 侧偏角角度很小
- 车辆匀速行驶
- 不考虑环境因素
再根据上述公式推导,得到横向动力学连续模型转换为可用的近似离散化模型
x ( k + 1 ) = A x + B u + C (20) x(k+1)=Ax+Bu+C \tag{20} x(k+1)=Ax+Bu+C(20)
式中,
A = [ 0 1 0 0 0 − 2 C a f + 2 C a r m V x 2 C a f + 2 C a r m − 2 C a f ℓ f − 2 C a r ℓ r m V x 0 0 0 1 0 − 2 C a f ℓ f − 2 C a r ℓ r I z V x 2 C a f ℓ f − 2 C a r ℓ r I z − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] , B = [ 0 2 C a f m 0 2 C a f ℓ f I z ] , C = [ 0 − V x − 2 C a f ℓ f − 2 C a r ℓ r m V x 0 − 2 C a f ℓ f 2 + 2 C a r ℓ r 2 I z V x ] φ ˙ d e s A=\begin{bmatrix} 0 && 1 && 0 && 0 \\ 0 && -\frac{2C_{af}+2C_{ar}}{mV_{x}} && \frac{2C_{af}+2C_{ar}}{m} && - \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{mV_{x}} \\ 0 && 0 && 0 && 1 \\ 0 && -\frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{I_{z}V_{x}} && \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{I_{z}} && -\frac{2C_{af}\ell_{f}^{2}+2C_{ar}\ell_{r}^{2}}{I_{z}V_{x}} \end{bmatrix},\\ B=\begin{bmatrix} 0 \\ \frac{2C_{af}}{m} \\ 0 \\ \frac{2C_{af}\ell_{f}}{I_{z}} \\ \end{bmatrix},\\ C=\begin{bmatrix} 0 \\ -V_{x}- \frac{2C_{af}\ell_{f}-2C_{ar}\ell_{r}}{mV_{x}} \\ 0 \\ -\frac{2C_{af}\ell_{f}^{2}+2C_{ar}\ell_{r}^{2}}{I_{z}V_{x}} \\ \end{bmatrix}\dot{\varphi}_{des} A=⎣⎢⎢⎢⎡00001−mVx2Caf+2Car0−IzVx2Cafℓf−2Carℓr0m2Caf+2Car0Iz2Cafℓf−2Carℓr0−mVx2Cafℓf−2Carℓr1−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤,B=⎣⎢⎢⎡0m2Caf0Iz2Cafℓf⎦⎥⎥⎤,C=⎣⎢⎢⎢⎡0−Vx−mVx2Cafℓf−2Carℓr0−IzVx2Cafℓf2+2Carℓr2⎦⎥⎥⎥⎤φ˙des
Apollo中的LQR控制就是基于此模型的,具体的LQR控制在另外一篇文章中有详细描述。
前馈控制
系统加入反馈后,发现还有一个问题,就是相关的项不一定收敛于0,为了解决这个问题,于是就再加入了一个前馈项来进行补偿。
δ f f = L / R + K v a y − k 3 [ ℓ r R − ℓ f 2 C a r m V x 2 R ℓ ] (21) \delta_{ff}=L/R+K_{v}a_{y}-k_3[\frac{\ell_r}{R}-\frac{\ell_{f}}{2C_{ar}}\frac{mV^{2}_{x}}{R\ell}] \tag{21} δff=L/R+Kvay−k3[Rℓr−2CarℓfRℓmVx2](21)
式中,
K v = ℓ r m 2 C a f ( ℓ f + ℓ r ) − ℓ f m 2 C a r ( ℓ f + ℓ r ) K_v=\frac{\ell_{r}m}{2C_{af}(\ell_f+\ell_r)}-\frac{\ell_{f}m}{2C_{ar}(\ell_f+\ell_r)} Kv=2Caf(ℓf+ℓr)ℓrm−2Car(ℓf+ℓr)ℓfm
a y = V x 2 / R a_y=V_{x}^{2}/R ay=Vx2/R。