2018深圳杯B题无限拓扑回传规划题解
前言
这是我第一次参加数学建模比赛,经过和队友几天(特别是在辛酸的520日)的通力合作,最终拿了个校奖,其中,由于建模期间同时沉迷于java,建模的语言没有采用建模常用语言matlab,我觉得matlab太不友好了,于是乎,所有的代码都是我亲自手写的,包括基础的聚类算法、各种模型类等,代码地址在文末,欢迎参考交流。
废话不多说,来看题目和题解。
题目:无限拓扑回传规划
- 背景介绍
在城区建设基站,传输光纤部署最后一公里的成本高,光纤到站率低,全球综合来看低于60%;如果使用微波传输,由于微波只能在LOS(视距)场景下部署,而城区场景中LOS信道比例低于50%。
在农村网建设基站,单站业务量低,收入低,ROI(投资回报率)差,运营商建站对成本较为敏感。卫星传输租金、光纤传输建设费用对于运营商是很大的负担,而如果使用微波传输,对于相当一部分站点需要提升铁塔高度来满足微波的LOS场景要求,铁塔费用的增加对于运营商来说同样是不小的负担。
Relay无线回传方案利用FDD LTE或TDDLTE制式承载来为站点回传,相对微波有较强的NLOS(非视距)传输能力,可以解决城区、农网等场景下的传统传输方式不可达的问题,同时在部分场景下也可以替代微波,有效降低站高,节省加站费用。
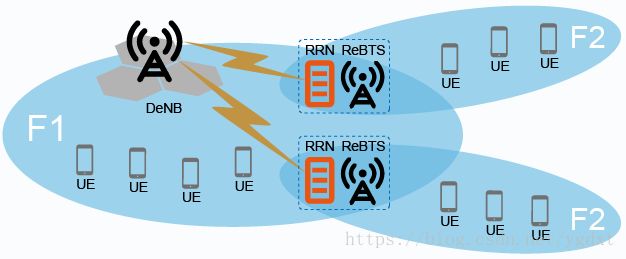
图1 Relay架构
RRN(eRelay Remote Node),是Relay方案中的无线回传设备,它用于为基站提供无线回传服务。如图1所示。Relay组网包含宿主基站DeNB和中继站RN两个逻辑节点:
- DeNB是在普通基站(DeNB)上增加了Relay功能,DeNB支持普通手机(UE)接入,也支持RRN的接入;
- RN包括RRN和ReBTS两部分。RRN通过无线信号接入DeNB并建立空口承载;ReBTS可供覆盖范围内的UE接入;ReBTS的传输由RRN提供
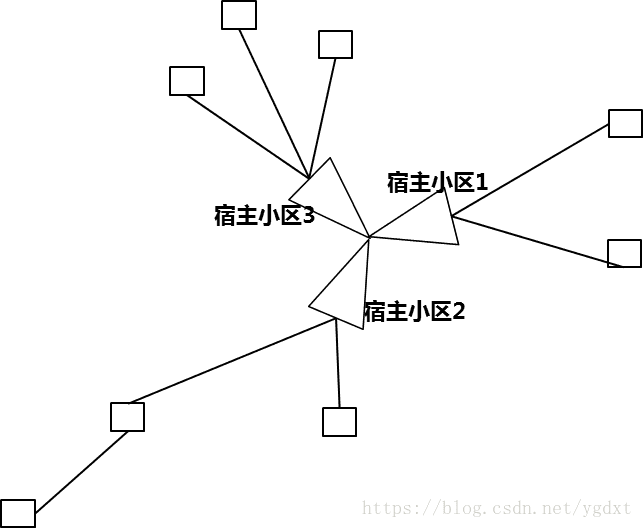
为了方便理解,这里分别将DeNB和RRN称作宿主站和子站,一个宿主基站通常可以有1~3个宿主小区,分别覆盖不同的方向(可理解为扇区的定义),如图2所示。图2中方块代表子站,每个宿主小区可以接入一定数量的子站,子站与子站之间可以级联(即多跳),但跳数有限制。
图2 Relay拓扑关系示意图
- 任务表述
2.1 任务简述
本任务中,在给定一个地区中候选站点的位置分布的情况下,参赛队伍需要根据站点间的相互位置、站点间拓扑关系限制等条件,在满足一定回传质量(本次任务仅根据宿主站与子站的距离是否满足某门限来判断是否满足最低回传质量要求。而实际Relay部署时,影响回传质量的因素包括距离、地形阻挡、普通手机接入影响、ReBTS干扰、相邻基站干扰等多种复杂因素)的前提下,设计成本最优的部站方案,包括:
- 候选站点是安装子站还是宿主站?
- 候选站点间的连接关系如何?
结合现网中对于无线回传拓扑规划问题的具体需求,算法还应该具有以下特点:算法收敛速度快、尽可能覆盖更多的站点。
2.2 输入输出
1、输入:
每个地区内,所有站点列表,包括:
- 站点经纬度;
- 站型:RuralStar或蝴蝶站;
各种站型的综合成本,包括:
- 宿主站的综合成本;
- 子站的综合成本;
- 卫星设备成本;
2、约束
输出的拓扑关系,应满足如下限制条件:
-
- 首跳距离≤20km,之后每跳距离≤10km
- 站点包含RuralStar和蝴蝶站两种不同站型;其中,RuralStar共包含1个扇区,蝴蝶站共包含2个扇区;若该站点为宿主站,则每个扇区第一级最大接入子站数4,最大总接入子站数6;为了简化问题,暂不考虑蝴蝶站的扇区覆盖方向;
- 宿主站之间采用微波连接,最大通信距离为50KM
- 宿主站和子站以及子站之间采用无线回传连接
- 每个子站最多只能有2条无线回传连接;
- 任意子站只能归属一个宿主站,到达所属宿主站有且只有一条通路,且该通路包含的跳数小于等于3
- 任意宿主站都有且只有一颗卫星负责回传,成片连接的宿主站可共享同一颗卫星,但一颗卫星最多只能负担8个成片宿主站的回传数据
- 成片宿主站中,宿主站总数不设上限
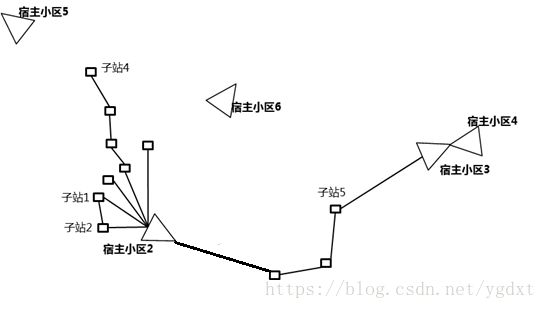
例如,如下图所示的连接关系中
- 宿主小区2不满足“每个扇区第一级最大接入数4,最大总接入数6”
- 子站1、子站2不满足“任意子站只能归属一个宿主站,到达所属宿主站有且只有一条通路”
- 子站4不满足“任意子站只能归属一个宿主站,到达所属宿主站有且只有一条通路,且该通路包含的跳数小于等于3”中的“跳数小于等于3”
- 子站5不满足“任意子站只能归属一个宿主站,到达所属宿主站有且只有一条通路,且该通路包含的跳数小于等于3”中的“任意子站只能归属一个宿主站”
上图连接关系可修改如下(前提是其它约束条件也满足),即可满足约束条件:
3、输出:
按输入数据中站点顺序,输出以下数据:
输出文件包含以下两个
Graph.csv
包含:
- 二维矩阵表示所有站点间的连接关系,0表示没有连接关系,1表示采用无线回传连接,2表示采用微波连接;
Posi.csv
包含以下数组,按列存储:
- 一维数组表示站点类型,0表示子站,1表示宿主站;
例如:
如上图所示的连接关系,以上数组将表述为:
|
|
宿主站1 |
宿主站2 |
宿主站3 |
子站1 |
子站2 |
子站3 |
子站4 |
子站5 |
子站6 |
子站7 |
子站8 |
| 宿主站1 |
0 |
2 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 宿主站2 |
2 |
0 |
2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
| 宿主站3 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
| 子站1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站2 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| 子站3 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站7 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 子站8 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 站点名 |
站点类型 |
| 宿主站1 |
1 |
| 宿主站2 |
1 |
| 宿主站3 |
1 |
| 子站1 |
0 |
| 子站2 |
0 |
| 子站3 |
0 |
| 子站4 |
0 |
| 子站5 |
0 |
| 子站6 |
0 |
| 子站7 |
0 |
| 子站8 |
0 |
算法效率:5分钟内
站点规模:1000站点左右
2.2 挑战目标
在拓扑架构满足约束条件的前提下,
挑战目标1(最高优先级):更低的总体成本
总体成本:宿主站数量*宿主站成本+子站数量*子站成本+卫星数量*卫星成本
平均成本=总体成本/地区内站点总数
这里,卫星的数量等于Ceil(宿主站数量/8),Ceil()表示向上取整。
下表为各种传输方式的成本,单位:W USD
| 宿主站成本 |
10 |
| 子站成本 |
5 |
| 卫星成本 |
50 |
挑战目标2:更低的回传路径损耗
虽然无线回传中存在NLOS影响,但为了简化问题,采用自由空间传播模型估计站点之间的路径损耗,公式如下:
PL=32.5+20*lg(D)+20*lg(F)
其中,PL是路径损耗,是两个站点之间的距离,D单位为km,F是发射频率,单位为MHz,这里默认采用900MHz。
系统平均损耗=所有无线回传连接的损耗之和/无线回传连接数
需要注意,该路径损耗只考虑子站回传部分,宿主站之间采用微波传输,只需满足距离限制,不计算该损耗。
附:球面距离公式
计算球面两点间距离的公式,设A点纬度β1,经度α1;B点纬度β2,经度α2,则距离S为:
S=R·arc cos[cosβ1cosβ2cos(α1-α2)+sinβ1sinβ2]
其中R为地球半径,本题中取6378km;
题解:
因为考虑到分组,最后采用了人工智能里常见的K-Means聚类方法来把子站按照距离最近原则分组。本人当时比较喜欢java,所有代码均采用java语言编写。
在具体实现过程中,所有输入数据均是符合条件的随机值,1000个站点大致随机分布在东经112.98~113.98和北纬28.12~28.24的公共区域内,1000个站点,每组最多12个,大致分为84组,这里就有两种思路了
思路一:
在第一次分区的时候不加限制每个区子站数,这样就可能有的区子站数会超过12个,超过12个的区再分簇,以此类推,直至符合条件,将所有符合条件的分区加入结果集。
思路二:
在第一次分区的时候限制每个区子站数最多为12个。
细细体会,觉得第一种思路好些,于是最后完成了思路一,思路二也做了大半,最后提交的是思路一。
算法核心思想:
算法的核心是K均值聚类和图的拓扑算法,K均值聚类主要用在分站点为以宿主站为中心包含合适数量的子站的若干个簇,拓扑算法主要用于连接每个簇内的子站和宿主站。
考虑到成本,采用这样的思路聚类:固定每个分区大小为12,后来输出数据和打印散点图时发现这样不满足首跳距离小于20Km等一系列约束条件;最后转而采用这样的思路进行聚类:先不设定分区大小,暂定分区数为84(1000/12),因为这样能保证相互距离最小的点分在一簇里,然后进行聚类,对聚类的结果进行分析,遍历蔟,如果簇满足约束条件,将该簇加入到结果集中;否则,则以该簇为聚类对象再聚类,再分析聚类结果(如,如果簇内站点数量超过12个,则构建模型分区数N = 站点数量/12(整除) + 1),类似于神经网络里的训练思想;这样,就能保证所有的簇都能满足约束条件,但是分区数不止84,因为在初始的84个簇里,不满足条件的已经进行裂变。
然后是图的拓扑算法,对结果集中的簇进行遍历,对每一个簇,先遍历每个子站并得到其与宿主站之间的距离,取距离最小的四个子站作为首跳,然后遍历剩下的子站,对于每一个剩下的子站,得到其与首跳的四个子站的距离,并与距离最小的那个首跳子站建立连接(采用矩阵无向图表示图),以此类推,构图完成。
代码地址
https://github.com/inspurer/MathematicalModeling
整个项目工程结果如下:
代码里有丰富的注释,代码、算法思想说明、运算结果结果csv文件都已上传到github,欢迎star,有问题欢迎评论