论文笔记：2004-Model Predictive Control of a Mobile Robot Using Linearization

摘要

提出了一种非完整约束轮式移动机器人的最优控制方案。
众所周知，具有非完整约束的wheeled mobile robot (WMR)不能通过连续可微的时不变控制律来反馈稳定。
利用模型预测控制（MPC），自然地得到了一个不连续的控制律。
MPC的主要优点之一是能够直接处理约束（由于状态或输入限制）。
二次规划（QP）通过对WMR误差模型的逐次线性化来求解线性MPC。

引言

移动机器人控制领域是近几十年来研究的热点。

尽管轮式移动机器人（WMR）的运动学模型显然很简单，但非完整约束的存在使得这些系统的稳定控制律设计面临相当大的挑战。

由于Brockett条件[1]，无法得到连续可微的时不变稳定反馈控制律。为了克服这些限制，大多数作品使用非光滑和时变控制律[2]-[6]。

关于WMRs鲁棒自适应控制的最新研究成果，见[7]，[8]。

然而，在实际的实现中，由于自然产生的对输入或状态的约束，很难获得良好的性能。以前引用的著作都没有考虑到这些限制。这可以通过使用模型预测控制（MPC）方案以简单的方式实现。

对于WMR来说，这是一个重要的问题，因为机器人的位置可以被限制在一个安全的操作区域内。通过考虑输入约束，可以产生与执行器限值相关的控制动作。

此外，动态系统到链式或幂形式的坐标变换不再是必需的，这使得MPC的调谐参数的选择更加直观。

针对WMR的非完整特性，MPC隐式地生成了分段连续（非光滑）控制律。

模型预测控制是利用系统的模型通过最小化目标函数来获得最优控制序列的一种最优控制策略。在每个采样间隔，该模型用于预测系统在预测范围内的行为。基于这些预测，目标函数相对于未来的输入序列最小化，因此需要对每个采样间隔求解一个约束优化问题。尽管预测和优化是在未来的时间范围内执行的，但只使用当前采样间隔的输入值，并且在下一个采样时间重复相同的过程。

这种机制被称为移动或后退地平线策略，参照时间窗口从一个采样时间向前移动到下一个采样时间的方式。对于复杂的、约束的、多变量的控制问题，MPC已经成为过程工业中公认的标准[9]。在许多情况下，当被控制的工厂足够慢，允许其实施时，它被使用[10]。然而，对于具有快速和/或非线性动力学的系统，由于需要大量的在线计算，这种技术的实现在适用性上仍然存在根本的限制[11]。

WMR的模型是非线性的。尽管非线性模型预测控制（NMPC）已经得到了很好的发展[10]、[12]、[13]，但所需的计算量远远高于线性模型预测控制。

在NMPC中，有一个非线性规划问题需要在线求解，它是非凸的，有大量的决策变量，全局最小值通常是不可能找到的[14]。

在本文中，我们提出了一个策略，以克服至少一部分这些问题。**基本思想是使用连续线性化方法，如[14]所述，产生通过线性MPC求解的系统的线性时变描述。**然后，以控制输入为决策变量，将优化问题转化为二次规划问题。由于这是一个凸问题，QP问题可以通过数值鲁棒解得到全局最优解。结果表明，即使是实时实现也是可能的。虽然MPC并不是一种新的控制方法，但处理WMRs的MPC的工作是最近的且较少的[15]–[17]。

WMR的运动学模型

考虑了由刚体和非变形车轮组成的移动机器人（见图1）。

假定车辆在平面上运动而不打滑，即车轮与地面之间存在纯滚动接触。

WMR的运动学模型：
$$\{\begin{array}{l}\dot{x}=v\cos \theta \\ \dot{y}=v\sin \theta \\ \dot{\theta }=w\end{array}\text{\hspace{1em}(1)}$$
写作更紧凑的形式：
$$\dot{\mathbf{x}}=f(\mathbf{x},\mathbf{u})\text{\hspace{1em}(2)}$$
$\mathbf{x}\triangleq {\left[\begin{array}{lll}x& y& \theta \end{array}\right]}^T$表示车轮中心$C$相对于全局惯性坐标系$\{O,X,Y\}$中的（configuration）配置（位置和方向）；

$\mathbf{u}\triangleq [vw{]}^T$是控制输入，其中$v$和$w$分别是线速度和角速度。

通过计算相对于参考车的误差模型得到线性模型。这样做。考虑同样由（2）描述的参考车。因此，它的轨迹${\mathbf{x}}_r$和${\mathbf{u}}_r$:
$${\dot{\mathbf{x}}}_r=f\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)\text{\hspace{1em}(3)}$$
通过在点$\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)$处展开式（2）的右侧，并丢弃高阶项，得到：
$$\begin{array}{r}\dot{\mathbf{x}}=f\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)+{\frac{\partial f(\mathbf{x},\mathbf{u})}{\partial \mathbf{x}}|}_{\genfrac{}{}{0ex}{}{\mathbf{x}={\mathbf{x}}_r}{\mathbf{u}={\mathbf{u}}_r}}\left(\mathbf{x}-{\mathbf{x}}_r\right)+{\frac{\partial f(\mathbf{x},\mathbf{u})}{\partial \mathbf{u}}|}_{\genfrac{}{}{0ex}{}{\mathbf{x}={\mathbf{x}}_r}{\mathbf{u}={\mathbf{u}}_r}}\left(\mathbf{u}-{\mathbf{u}}_r\right)\end{array}\text{\hspace{1em}(4)}$$
或者，表示为：
$$\dot{\mathbf{x}}=f\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)+f_{\mathbf{x},r}\left(\mathbf{x}-{\mathbf{x}}_r\right)+f_{\mathbf{u},r}\left(\mathbf{u}-{\mathbf{u}}_r\right)\text{\hspace{1em}(5)}$$
其中，$f_{\mathbf{x},r}$和$f_{\mathbf{u},r}$分别表示$f$对于$x$和$u$的雅各比矩阵，分别在参考点$\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)$周围计算。

运动学模型参考论文：

[18] G. Campion, G. Bastin, and B. D’Andr´ea-Novel, “Structural properties and classification of kinematic and dynamical models ofwheeled mobile robots,” IEEE Transactions on Robotics and Automation, vol. 12, no. 1, pp. 47–62, Feb 1996.

然后，用式5减去式3，可得：
$$\dot{\tilde{\mathbf{x}}}=f_{\mathbf{x},r}\tilde{\mathbf{x}}+f_{\mathbf{u},r}\tilde{\mathbf{u}}\text{\hspace{1em}(6)}$$
$\tilde{\mathbf{x}}\triangleq \mathbf{x}-{\mathbf{x}}_r$表示相对于参考车辆的误差；

$\tilde{\mathbf{u}}\triangleq \mathbf{u}-{\mathbf{u}}_r$是其相关的扰动控制输入。

利用前向差分对$\dot{\mathbf{x}}$的近似给出了如下离散时间系统模型：
$$\tilde{\mathbf{x}}(k+1)=\mathbf{A}(k)\tilde{\mathbf{x}}(k)+\mathbf{B}(k)\tilde{\mathbf{u}}(k)\text{\hspace{1em}(7)}$$
其中：$T$是采样周期，$k$是采样时间。
$$\begin{array}{l}\mathbf{A}(k)\triangleq \left[\begin{array}{ccc}1& 0& -v_r(k)\sin {\theta }_r(k)T\\ 0& 1& v_r(k)\cos {\theta }_r(k)T\\ 0& 0& 1\end{array}\right]\\ \mathbf{B}(k)\triangleq \left[\begin{array}{cc}\cos {\theta }_r(k)T& 0\\ \sin {\theta }_r(k)T& 0\\ 0& T\end{array}\right]\end{array}$$
实际上，$x$收敛到$x_r$，相当于$\tilde{\mathbf{x}}$收敛到集合$\mathcal{O}=\{\mathbf{x}|(\tilde{x},\tilde{y},\tilde{\theta })=(0,0,2\pi n)\},n\in \{0,\pm 1,\pm 2,\dots \}$

文献[2]证明了非线性非完整系统（1）是完全可控的，即它可以在有限时间内用有限的输入从任何初始状态转向任何最终状态。

很容易看出，当机器人不运动时，固定工作点的线性化是不可控的。

然而，只要控制输入$u$不为零，这种线性化就可以控制[3]。

这意味着可以使用线性MPC[17]跟踪参考轨迹。

[2] A. M. Bloch and N. H. McClamroch, “Control of mechanical systems with classical nonholonomic constraint,” in American Conference on Decision and Control, Tampa, Florida, 1989, pp. 201–205…

[3] C. Samson and K. Ait-Abderrahim, “Feedback control of a nonholonomic wheeled cart in cartesian space,” in IEEE Int. Conf. on Robotics and Automation, Sacramento, California, 1991, pp. 1136–1141

[17] H. V. Essen and H. Nijmeijer, “Non-linear model predictive control of constrained mobile robots,” in European Control Conference, Porto, Portugal, 2001, pp. 1157–1162

MPC算法

在第一节中，MPC方案的本质是在一系列未来控制输入上优化过程行为的预测。这样的预测是通过使用一个过程模型在一个有限的时间间隔内完成的，称为预测时域prediction horizon。在每个采样时刻，模型预测控制器通过求解一个优化问题生成一个最优控制序列。该序列的第一个元素应用于模型。在下一次采样时，使用更新的过程测量值和移动的视界horizon再次解决该问题。

为了简单起见，我们假设在这项工作中，设备的状态始终可用于测量，并且不存在模型不匹配。

要最小化的目标函数可以表示为状态和控制输入的二次函数：
$$\begin{array}{r}\Phi (k)=\sum _{j=1}^N{\tilde{\mathbf{x}}}^T(k+j|k)\mathbf{Q}\tilde{\mathbf{x}}(k+j|k)+{\tilde{\mathbf{u}}}^T(k+j-1|k)\mathbf{R}\tilde{\mathbf{u}}(k+j-1|k)\end{array}\text{\hspace{1em}(8)}$$
其中$N$是预测时域，$Q，R$是加权矩阵，同时要求$Q>0，R>0$。记号$a(m|n)$表示在$n$时刻预测的$m$时刻的$a$的值。注意：此处是$\tilde{\mathbf{x}}(k+j|k)$，而$\tilde{\mathbf{u}}(k+j-1|k)$，两者之间相差一个时刻。

优化问题可以表述为找到${\tilde{\mathbf{u}}}^{\star }$，使得：
$${\tilde{\mathbf{u}}}^{\ast }=\arg \underset{\tilde{\mathbf{u}}}{\min }\{\Phi (k)\}\text{\hspace{1em}(9)}$$
在每个时刻$k$求解最小化（8）的问题，得到一个最优控制序列$\{{\tilde{\mathbf{u}}}^{\star }(k|k),\cdots ,{\tilde{\mathbf{u}}}^{\star }(k+N-1|k)\}$和最优成本cost${\Phi }^{\star }(k)$。MPC控制律由最优控制序列${\tilde{\mathbf{u}}}^{\star }(k|k)$的第一个控制动作隐式给出。

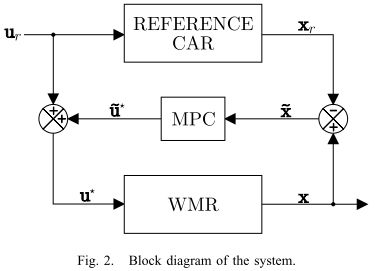
包含系统中所有单元的方框图如图2所示。图中省略了索引$(k|k)$。

为了用一种常见的二次规划的形式重新描述优化问题，我们引入以下向量：
$$\overline{\mathbf{x}}(k+1)\triangleq \left[\begin{array}{c}\tilde{\mathbf{x}}(k+1|k)\\ \tilde{\mathbf{x}}(k+2|k)\\ ⋮\\ \tilde{\mathbf{x}}(k+N|k)\end{array}\right]\overline{\mathbf{u}}(k)\triangleq \left[\begin{array}{c}\tilde{\mathbf{u}}(k|k)\\ \tilde{\mathbf{u}}(k+1|k)\\ ⋮\\ \tilde{\mathbf{u}}(k+N-1|k)\end{array}\right]$$
因此，式8可以重新被写作：
$$\Phi (k)={\overline{\mathbf{x}}}^T(k+1)\overline{\mathbf{Q}}\overline{\mathbf{x}}(k+1)+{\overline{\mathbf{u}}}^T(k)\overline{\mathbf{R}}\overline{\mathbf{u}}(k)\text{\hspace{1em}(10)}$$
其中：
$$\overline{\mathbf{Q}}\triangleq \left[\begin{array}{cccc}\mathbf{Q}& 0& \cdots & 0\\ 0& \mathbf{Q}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \mathbf{Q}\end{array}\right]\overline{\mathbf{R}}\triangleq \left[\begin{array}{cccc}\mathbf{R}& 0& \cdots & 0\\ 0& \mathbf{R}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \mathbf{R}\end{array}\right]$$
因此，结合式7可以将$\overline{\mathbf{x}}(k+1)$写作：
$$\overline{\mathbf{x}}(k+1)=\overline{\mathbf{A}}(k)\tilde{\mathbf{x}}(k|k)+\overline{\mathbf{B}}(k)\overline{\mathbf{u}}(k)\text{\hspace{1em}(11)}$$
其中：
$$\overline{\mathbf{A}}(k)\triangleq \left[\begin{array}{c}\mathbf{A}(k|k)\\ \mathbf{A}(k|k)\mathbf{A}(k+1|k)\\ ⋮\\ \alpha (k,0)\end{array}\right]$$

$$\begin{array}{l}\mathbf{B}(k)\triangleq \left[\begin{array}{ccccc}\mathbf{B}(k|k)& 0& \cdots & 0& \\ \mathbf{A}(k+1|k)\mathbf{B}(k|k)& \mathbf{B}(k+1|k)& \cdots & 0& \\ ⋮& ⋮& \ddots & ⋮& \\ \alpha (k,1)\mathbf{B}(k|k)& \alpha (k,2)\mathbf{B}(k+1|k)& \cdots & \mathbf{B}(k+N-1|k)& \end{array}\right]\end{array}$$

其中$\alpha (k,j)$被定义为：
$$\alpha (k,j)\triangleq \prod _{i=j}^{N-1}\mathbf{A}(k+i|k)$$
根据式10和式11，可以将目标函数式8重写为标准的二次形式：
$$\Phi (k)=\frac{1}{2}{\overline{\mathbf{u}}}^T(k)\mathbf{H}(k)\overline{\mathbf{u}}(k)+{\mathbf{f}}^T(k)\overline{\mathbf{u}}(k)+\mathbf{d}(k)$$
其中：
$$\begin{array}{rl}\mathbf{H}(k)& \triangleq 2\left(\overline{\mathbf{B}}(k{)}^T\overline{\mathbf{Q}}\overline{\mathbf{B}}(k)+\overline{\mathbf{R}}\right)\\ \mathbf{f}(k)& \triangleq 2{\overline{\mathbf{B}}}^T(k)\overline{\mathbf{Q}}\overline{\mathbf{A}}(k)\tilde{\mathbf{x}}(k|k)\\ \mathbf{d}(k)& \triangleq {\tilde{\mathbf{x}}}^T(k|k){\overline{\mathbf{A}}}^T(k)\overline{\mathbf{Q}}\overline{\mathbf{A}}(k)\tilde{\mathbf{x}}(k|k)\end{array}$$
说明：矩阵$H$是Hessian矩阵，必须是正定的。它描述了目标函数的二次部分，向量$f$描述了线性部分。$d$独立于$\tilde{\mathbf{u}}$，与${\mathbf{u}}^{\ast }$的决定无关。

**模型预测控制是基于对小时间范围内的对象和模型行为相同的假设。**为了保持这种假设，模型的不匹配应保持较小。显然，对于任何真实世界的模型，控制输入都受到物理限制。因此，在计算控制输入时，应考虑这些限制，以避免大型设备/模型失配。这可以通过在控制输入上定义上下界以简单的方式完成。解决优化问题，必须同时确保将控制输入保持在上下界之间。因此，控制约束可以写作：
$${\mathbf{u}}_{\min }(k)\le \mathbf{u}(k)\le {\mathbf{u}}_{\max }(k)\text{\hspace{1em}(12)}$$
其中下标$min$和$max$分别表示下界和上界，（9）中的优化问题可以重新公式化为找${\tilde{\mathbf{u}}}^{\star }$使得：
$${\tilde{\mathbf{u}}}^{\star }=\arg \underset{\tilde{\mathbf{u}}}{\min }\{\Phi (k)\}\text{\hspace{1em}(13)}$$
使得：
$$\mathbf{D}\tilde{\mathbf{u}}\le \mathbf{d}\text{\hspace{1em}(14)}$$
其中$\Phi (k)$是目标函数，$\tilde{\mathbf{u}}$是优化不等式（14）中的自由变量，不等式14是描述控制变量中约束的一种通用方法。例如只有式（12）所述的控制振幅约束时，我们有：
$$\left[\begin{array}{c}\mathbf{I}\\ -\mathbf{I}\end{array}\right]\tilde{\mathbf{u}}\le \left[\begin{array}{c}{\tilde{\mathbf{u}}}_{\max }\\ -{\tilde{\mathbf{u}}}_{\min }\end{array}\right]$$
即表示：${\tilde{\mathbf{u}}}_{min}\le \tilde{\mathbf{u}}\le {\tilde{\mathbf{u}}}_{max}$。

因为优化中的自由变量是$\tilde{\mathbf{u}}(k)$，限制12需要关于此变量重写为：
$${\mathbf{u}}_{\min }(k)-{\mathbf{u}}_r(k)\le \tilde{\mathbf{u}}(k)\le {\mathbf{u}}_{\max }(k)-{\mathbf{u}}_r(k)$$
其中：
$$\begin{array}{ccccc}{\overline{\mathbf{u}}}_{\min }(k)\triangleq \left[\begin{array}{c}{\mathbf{u}}_{\min }(k)\\ {\mathbf{u}}_{\min }(k+1)\\ ⋮\\ {\mathbf{u}}_{\min }(k+N-1)\end{array}\right]& & {\overline{\mathbf{u}}}_{\max }(k)\triangleq \left[\begin{array}{c}{\mathbf{u}}_{\max }(k)\\ {\mathbf{u}}_{\max }(k+1)\\ ⋮\\ {\mathbf{u}}_{\max }(k+N-1)\end{array}\right]& & {\mathbf{u}}_r(k)\triangleq \left[\begin{array}{c}{\mathbf{u}}_r(k)\\ {\mathbf{u}}_r(k+1)\\ ⋮\\ {\mathbf{u}}_r(k+N-1)\end{array}\right]\end{array}$$
由于状态预测是要计算的最优序列的函数，所以很容易证明状态约束也可以用（14）来一般地描述。此外，控制和状态变化率的约束也可以用类似的方式表示。

仿真结果

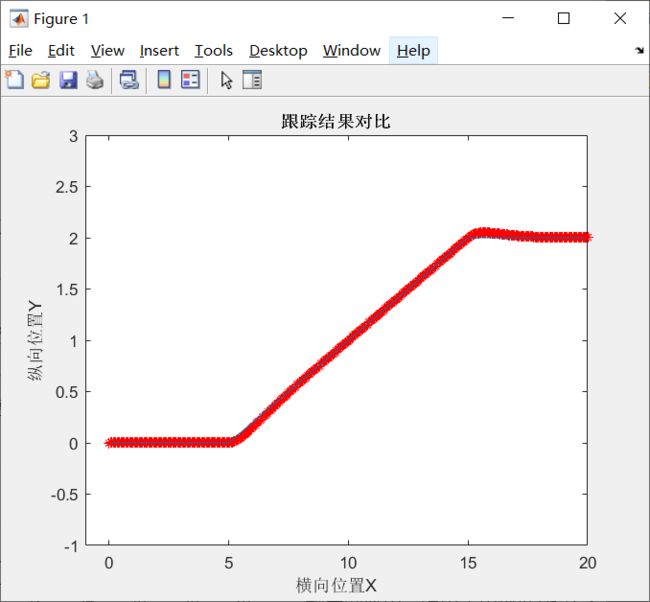
论文中跟踪曲线为8字型曲线，曲率是连续的，此处跟踪一个折线段，因为实际运行时的角度不能突变，所以在转弯处会有一个调节过程。

结论

本文介绍了MPC在非完整WMR轨迹跟踪问题中的应用。给出了用标准QP法求解优化问题的方法。所获得的控制信号使得施加在控制变量上的约束得以成立。

MPC的一些优点：

• 可以直接处理状态/输入约束；
• 不需要坐标转换为链式或幂形式；
• MPC隐式生成分段连续控制律，从而处理Brockett条件。

结果表明，采用逐次线性化方法，最优控制问题得到了成功的解决，从而产生了实时实现的可能性。利用这种技术，可以将优化问题转化为一个标准的QP公式，该公式计算速度快，且具有很强的鲁棒性。

参考链接

quadprog

二次规划问题和MATLAB函数quadprog的使用

二次规划的MATLAB解法：quadprog函数

dsolve函数

matlab eval函数的使用