机器学习中的ROC曲线与AUC指标的意义与代码实现

ROC曲线与AUC指标是机器学习中的常用评价方法。
ROC曲线与AUC指标理解

混淆矩阵：

TP = True Postive = 真正例（真阳性）；
FP = False Positive = 假正例（假阳性）；
FN = False Negative = 假负例（假阴性）；
TN = True Negative = 真负例（真阴性）。

ROC曲线

用来绘制ROC曲线的纵坐标是TPR（True Positive Rate），横坐标是FPR（False Positive Rate）：

指标	意义
FPR（假正例率）	FP / ( FP + TN ) = FP / F（真实值为负例，而预测为正例的比例）
TPR（真正例率）	TP / ( TP+FN ) = TP / T （真实值是正例，且预测为正例的比例）（同召回率）

绘制方法

机器学习的的输出是对样本的一个实值或概率预测，然后将这个预测值与一个分类阈值进行比较，若大于阈值分为正类，否则为反类，分类阈值即为截断点。（比如截取点为0.5，大于0.5为正例，小于0.5为负例）

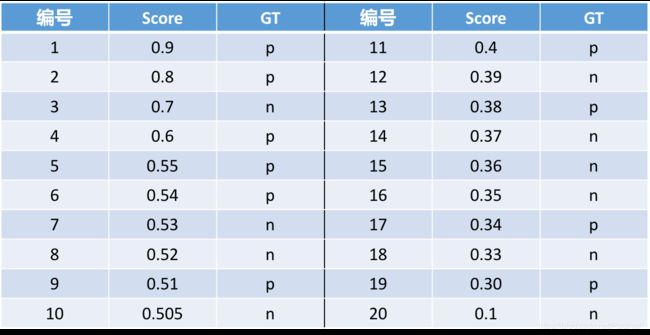
比如有一组数据如下。把学习器输出的，该样本为正例的概率，记为Score。GT即GroundTruth，即样本真实分类。

1.按Score从大到小排列。

2.依次对每个阈值计算FPR、TPR

每次取的分类阈值即为当前Score值（比如第一次取1，第二次取0.9，第三次取0.8，以此类推）。然后每次以当前Score作为截断点对所有样本的预测概率进行归类，根据该分类计算当前的FPR、TPR。

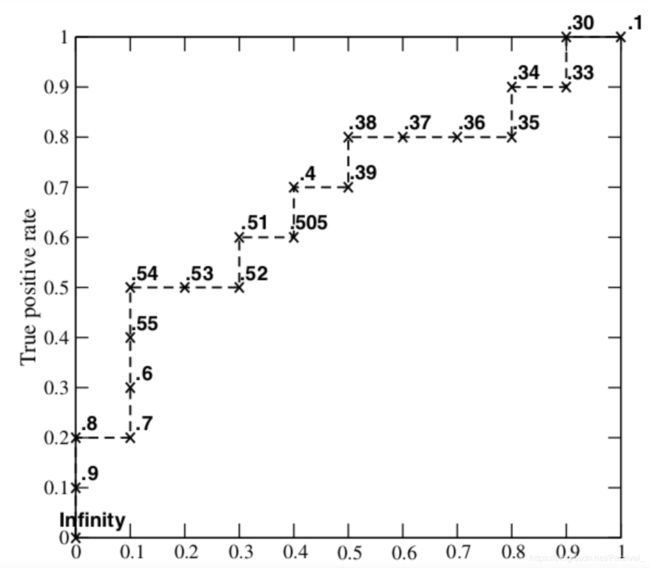
图中曲线上标的数字即为当前使用的分类阈值（截断点）。

代码

获取分类阈值（截断点）：

import numpy as np
from sklearn.metrics import roc_curve

gt = np.array([0,1,0,1,0,0,0,1,0,1,0,1,0,0,1,1,1,0,1,1]) 
scores = np.array([0.1,0.3,0.33,0.34,0.35,0.36,0.37,0.38,0.39,0.4,0.505,0.51,0.52,0.53,0.54,0.55,0.6,0.7,0.8,0.9])
fpr, tpr, thresholds = roc_curve(gt, scores, pos_label=1) # 设置正标签为1
print(fpr)
print(tpr)
print(thresholds)

结果：

[0.  0.  0.  0.1 0.1 0.3 0.3 0.4 0.4 0.5 0.5 0.8 0.8 0.9 0.9 1. ]
[0.  0.1 0.2 0.2 0.5 0.5 0.6 0.6 0.7 0.7 0.8 0.8 0.9 0.9 1.  1. ]
[1.9   0.9   0.8   0.7   0.54  0.52  0.51  0.505 0.4   0.39  0.38  0.35
 0.34  0.33  0.3   0.1  ]

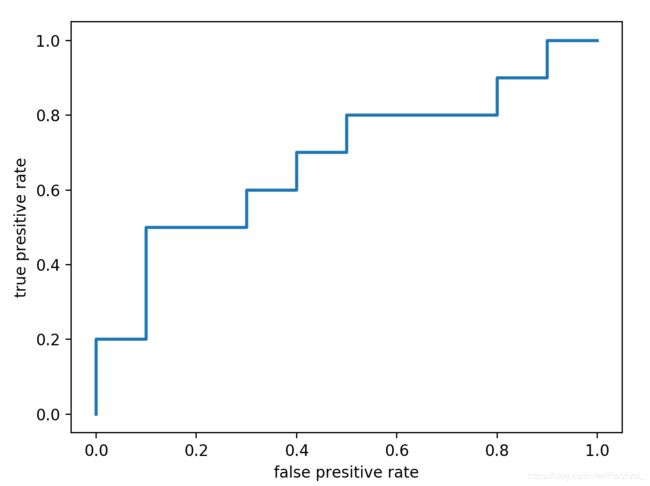
可视化：

plt.plot(fpr,tpr,linewidth=2,label="ROC")
plt.xlabel("false presitive rate")
plt.ylabel("true presitive rate")

plt.show()

结果：

计算AUC

from sklearn.metrics import roc_auc_score

auc = roc_auc_score(gt, scores)
print(auc)

结果

0.6799999999999999

ROC与PR曲线相比

两者区别：

曲线	区别
ROC曲线	FPR为横坐标，TPR为纵坐标
PR曲线	recall为横坐标，precision 为纵坐标

其中：

指标	计算
精确率(precision)	TP / ( TP+FP ) = TP / P
召回率(recall）	TP / (TP + FN ) = TP / T

精确度意义：预测为正例的样本中真实正例比例（查准）。
召回率意义：所有真实正例中被预测为正例的比例(查全）。

精确率(precision) 与召回率(recall)的理解

正负样本分布发生变化时，PR曲线会有较大改变。ROC曲线变化不大。