陈宝林《最优化理论与算法》超详细学习笔记 (二)————补充知识(凸集) & 第二章 线性规划的基本性质
陈宝林《最优化理论与算法》超详细学习笔记 (二)————补充知识 凸集 & 第二章 线性规划的基本性质
- 补充知识
- 凸集
- 方向与极方向
- 表示定理
- 择一定理
- 第一章 线性规划的基本性质
- 问题的提出
- 图解法
- 标准型
- 线性规划问题的解概念
补充知识
凸集
设 S 为 n 维欧氏空间 R n R^n Rn中一个集合。 若对 S 中任意两点,联结它们的线既仍属于 S; 换言之,对 S 中任意两点 x ( 1 ) , x ( 2 ) \bf{x}^{(1)},\bf{x}^{(2)} x(1),x(2) 及每个实数
λ ∈ [ 0 , 1 ] \lambda \in[0, \quad1] λ∈[0,1] 都有:
λ x ( 1 ) + ( 1 − λ ) x ( 2 ) ∈ S \lambda x^{(1)}+(1-\lambda) x^{(2)} \in S λx(1)+(1−λ)x(2)∈S
则称 S 为凸集, λ x ( 1 ) + ( 1 − λ ) x ( 2 ) \lambda x^{(1)}+(1-\lambda)x^{(2)} λx(1)+(1−λ)x(2)称为凸组合.

如图(a)是凸集,而图(b)不是.
方向与极方向
设S为 R n R^n Rn中闭四集,d为非零向量,如果对S中的每一个x都 有 射 线 { x + λ d ∣ λ ≥ 0 } ∈ S \{\mathrm{ x} + \lambda d | ~ \lambda \geq 0 \}\in S {x+λd∣ λ≥0}∈S , 则 称 d 为 S 的 一 个 方 向 。
设d是S的两个方向,若S不能表示成该集合的两个不同 方向的正线性组合,则称d为S的极方向.
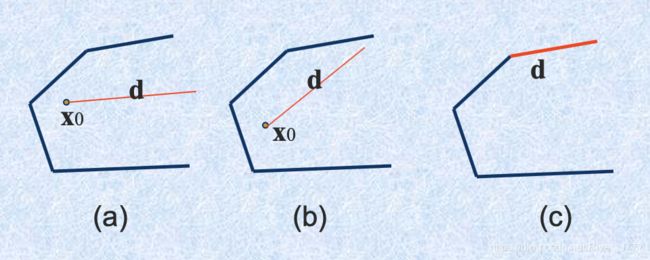
如图(a)中d是一个方向,图©中与边界重合的d是一个极方向,图(b)中d则既不是方向也不是极方向.
表示定理
设 S = { x ∣ A x = b , x ≥ 0 } \mathrm{~S = \{ x |A x = b , x \geq 0 \} ~} S={x∣Ax=b,x≥0} 为 非 空 多 面 集 , 则 有 :
(1)P的极点集K是非空的有限集合,记为 { x ( 1 ) , x ( 2 ) , x ( k ) } \{ \left.x^{(1)}, \mathbf{x}^{(2)}, \mathbf{x}^{(k)}\right\} {x(1),x(2),x(k)}
(2)设S的极方向集为J,则指标集J是空集当且仅当S是有界 集合,即多胞形.
(3) x ∈ S x \in S x∈S的充要条件为:
x = ∑ k ∈ K λ k x k + ∑ j ∈ J μ j d j x=\sum_{k \in K} \lambda_{k} x^{k}+\sum_{j \in J} \mu_{j} d^{j} x=k∈K∑λkxk+j∈J∑μjdj
其中 ∑ k ∈ K λ k = 1 , λ k ≥ 0 , k ∈ K , μ j ≥ 0 , j ∈ J \sum_{k \in K} \lambda_{k}=1, \lambda_{k} \geq 0, k \in K, \mu_{j} \geq 0, j \in J k∈K∑λk=1,λk≥0,k∈K,μj≥0,j∈J
择一定理
- Farkas定理
设A为 m × n m \times n m×n矩阵,c为n维向量,则 A x ≤ 0 , c T x > 0 A x \leq 0, \quad c^{T} x>0 Ax≤0,cTx>0 有解的充要条件是, A T y = c , y ≥ 0 A^{T} y=c, y \geq 0 ATy=c,y≥0 无解. - Gordan定理
设A为 m × n m \times n m×n矩阵,那么, A x < 0 Ax<0 Ax<0有解的充要条件是不存在非零向量 y ≥ 0 y \geq0 y≥0,使 A ′ y = 0 A'y=0 A′y=0.
证明略.
第一章 线性规划的基本性质
问题的提出
例 某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示
| 产品1 | 产品2 | 拥有量 | |
|---|---|---|---|
| 设备 | 1 | 2 | 8台时 |
| 原材料A | 4 | 0 | 16kg |
| 原材料B | 0 | 4 | 12kg |
每生产一件产品1可获利2元,每生产一件产品2可获利3元,问应如何安排计划使该工厂获利最多?
根据题目:
- 设 x 1 , x 2 x_{1}, x_{2} x1,x2 分别表示计划生产I,II产品的数量, 称它们为决策变量;
- 生产 x 1 , x 2 x_{1}, x_{2} x1,x2 的数量多少,受资源押有量的限制 这是约束条件,即x_ + 2 x 2 ≤ 8 ; 4 x 1 ≤ 16 ; 4 x 2 ≤ 12 +2 x_{2} \leq 8 ; 4 x_{1} \leq 16 ; 4 x_{2} \leq 12 +2x2≤8;4x1≤16;4x2≤12;
- 生产的产品不能是负值,即x_, x 2 ≥ 0 x_{2} \geq 0 x2≥0;
- 如何安排生产,使利润最大,这是目标.
用数学关系式可以表达为:
目标函数 max z = 2 x 1 + 3 x 2 \quad \max z=2 x_{1}+3 x_{2} maxz=2x1+3x2
约束条件: { x 1 + 2 x 2 ≤ 8 4 x 1 ≤ 16 4 x 2 ≤ 12 x 1 , x 2 ≥ 0 \left\{\begin{array}{rr}x_{1}+2 x_{2} \leq 8 \\ 4 x_{1} \quad \quad \leq 16 \\ 4 x_{2} \leq 12 \\ x_{1}, x_{2} \geq 0\end{array}\right. ⎩⎪⎪⎨⎪⎪⎧x1+2x2≤84x1≤164x2≤12x1,x2≥0
这就是一个最简单的线性规划问题.
我们可以发现:
- 每一个线性规划问题都用一组决策变量 ( x 1 , x 2 , ⋯ x n ) \left(x_{1}, x_{2}, \cdots x_{n}\right) (x1,x2,⋯xn)
表示某一方案,这组决策变量的值代表一个具体方案。一般这些变量的取值是非负且连续的; - 都有关于各种资源和资源使用情况的技术数据,创造新 价值的数据:
a i j ; c j ( i = 1 , ⋯ m ; j = 1 , ⋯ n ) a_{i j} ; c_{j}(i=1, \cdots m ; j=1, \cdots n) aij;cj(i=1,⋯m;j=1,⋯n) - 存在可以量化的约束条件,这些约束条件可以用一组线 性等式或线性不等式来表示;
- 都有一个达到某一目标的要求,可用决策变量的线性函 数(称为目标函数) 来表示。按问题的要求不同,要求目标函数实现最大化或最小化。
线性规划模型的一般形式
目标函数
max ( min ) z = c 1 x 1 + c 2 x 2 + ⋯ + c n x n \max (\min ) z=c_{1} x_{1}+c_{2} x_{2}+\cdots+c_{n} x_{n} max(min)z=c1x1+c2x2+⋯+cnxn
约束条件
a 11 x 1 + a 12 x 2 + ⋯ ⋯ + a 1 n x n ≤ ( = , ≥ ) b 1 a_{11} x_{1}+a_{12} x_{2}+\cdots \cdots+a_{1 n} x_{n} \leq(=, \geq) b_{1} a11x1+a12x2+⋯⋯+a1nxn≤(=,≥)b1
a 21 x 1 + a 22 x 2 + ⋯ ⋯ + a 2 n x n ≤ ( = , ≥ ) b 2 a_{21} x_{1}+a_{22} x_{2}+\cdots \cdots+a_{2 n} x_{n} \leq(=, \geq) b_{2} a21x1+a22x2+⋯⋯+a2nxn≤(=,≥)b2
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ \cdot \cdot \cdot \cdot \cdot \cdot ⋅⋅⋅⋅⋅⋅
a m 1 x 1 + a m 2 x 2 + ⋯ ⋯ + a m x n ≤ ( = , ≥ ) b m a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots \cdots+a_{m} x_{n} \leq(=, \geq) b_{m} am1x1+am2x2+⋯⋯+amxn≤(=,≥)bm
x 1 , x 2 , ⋯ ⋯ , x n ≥ 0 x_{1}, x_{2}, \cdots \cdots, x_{n} \geq 0 x1,x2,⋯⋯,xn≥0
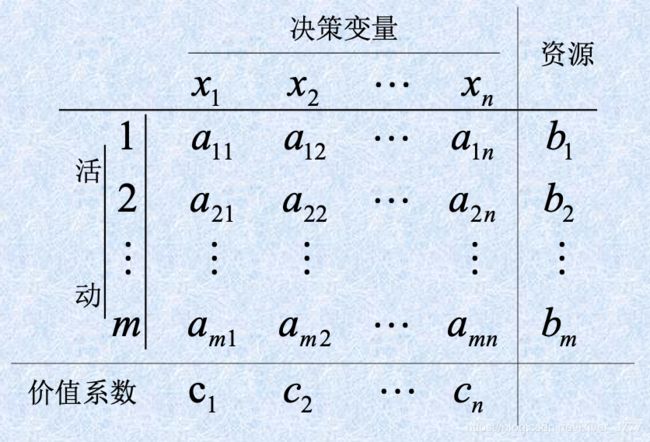
用表格形式可以表示为:
图解法
同样是以上面的例题为例,
目标函数 max z = 2 x 1 + 3 x 2 \quad \max z=2 x_{1}+3 x_{2} maxz=2x1+3x2
约束条件: { x 1 + 2 x 2 ≤ 8 4 x 1 ≤ 16 4 x 2 ≤ 12 x 1 , x 2 ≥ 0 \left\{\begin{array}{rr}x_{1}+2 x_{2} \leq 8 \\ 4 x_{1} \quad \quad \leq 16 \\ 4 x_{2} \leq 12 \\ x_{1}, x_{2} \geq 0\end{array}\right. ⎩⎪⎪⎨⎪⎪⎧x1+2x2≤84x1≤164x2≤12x1,x2≥0
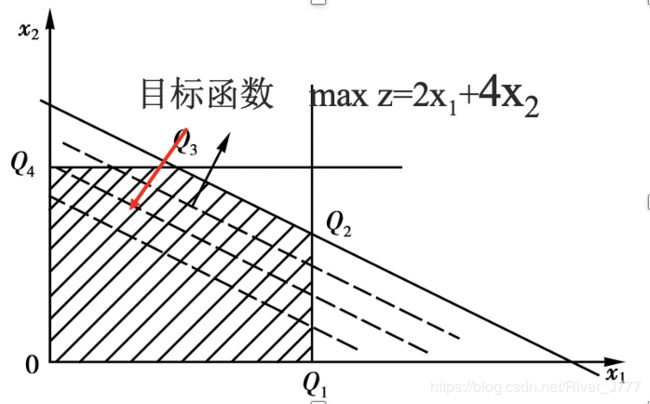
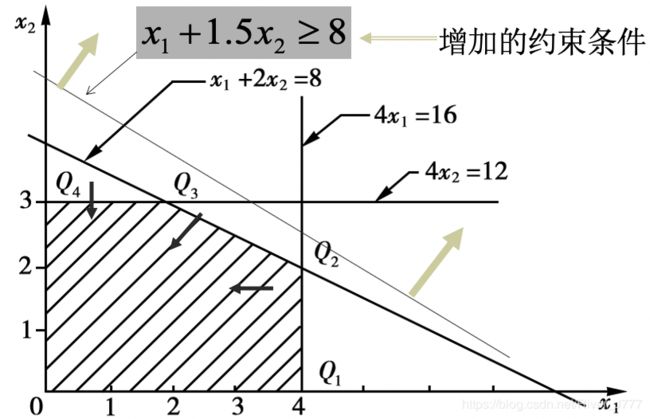
我们可以画出图形,如下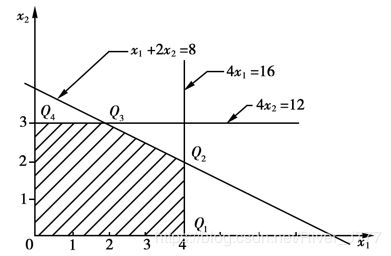
以斜率 − 2 3 -\frac{2}{3} −32作出一簇直线,见虚线,虚线在y轴上的纵截距为目标函数值z的 1 3 \frac{1}{3} 31,即 z 3 \frac{z}{3} 3z
不难看出,目标值在(4,2)点,达到最大值14.
通过图解法,可观察到线性规划的解可能出现 的几种情况:
标准型
线性规划问题的标准型式如下:
目标函数: max z = c 1 x 1 + c 2 x 2 + ⋯ + c n x n 约束条件: { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b n x 1 , x 2 , ⋯ , x n ≥ 0 \begin{aligned} &\text { 目标函数: } \max z=c_{1} x_{1}+c_{2} x_{2}+\cdots+c_{n} x_{n}\\ &\text { 约束条件: }\left\{\begin{array}{c} \mathrm{a}_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}=b_{2} \\ \cdots \cdots \cdots \cdots \\ a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n}=b_{n} \\ x_{1}, x_{2}, \cdots, x_{n} \geq 0 \end{array}\right. \end{aligned} 目标函数: maxz=c1x1+c2x2+⋯+cnxn 约束条件: ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯am1x1+am2x2+⋯+amnxn=bnx1,x2,⋯,xn≥0
需要注意的地方有
- 目标函数求最大值;
- 约束条件中均为等号;
- 约束条件中b大于等于零;
- 约束条件中x大于等于零;
那么如何将一般的线性规划问题转化为标准型呢?
(1) 若要求目标函数实现最小化,即min z = C X , z=C X, z=CX, 则只需将目标函数最小 化变换求目标函数最大化,即令 z ′ = − z z'= -z z′=−z,于是得到 m a x z ′ = − C X max z'= - CX maxz′=−CX.
(2) 约束条件为不等式。分两种情况讨论:
∙ \bullet ∙若约束条件为“ ≤ \leq ≤”型不等式,则可在不等式左端加入非负松他变量, 把原 ≤ \leq ≤型不等式变为等式约束;
∙ \bullet ∙若约束条件为 ≥ \geq ≥型不等式,则可在不等式左端减去一个非负剩余 变量(也称松他变量),把不等式约束条件变为等式约束。
(3) 若存在取值无约束的变量 x k x_{k} xk 可令
x k = x k ′ − x k ′ ′ x k ′ , x k ′ ′ ≥ 0 \begin{array}{l} x_{k}=x_{k}^{\prime}-x_{k}^{\prime \prime} \\ x_{k}^{\prime}, x_{k}^{\prime \prime} \geq 0 \end{array} xk=xk′−xk′′xk′,xk′′≥0
例2:
将下述线性规划问题化为标准形式
min z = − x 1 + 2 x 2 − 3 x 3 { x 1 + x 2 + x 3 ≤ 7 x 1 − x 2 + x 3 ≥ 3 − 3 x 1 + x 2 + x 3 = 5 x 1 , x 2 ≥ 0 ; x 3 为无约束 \begin{array}{c} \min z=-x_{1}+2 x_{2}-3 x_{3} \\ \left\{\begin{array}{c} x_{1}+x_{2}+x_{3} \leq 7 \\ x_{1}-x_{2}+x_{3} \geq 3 \\ -3 x_{1}+x_{2}+x_{3}=5 \\ x_{1}, x_{2} \geq 0 ; x_{3} \text { 为无约束 } \end{array}\right. \end{array} minz=−x1+2x2−3x3⎩⎪⎪⎨⎪⎪⎧x1+x2+x3≤7x1−x2+x3≥3−3x1+x2+x3=5x1,x2≥0;x3 为无约束
步骤:
- 用 x 4 − x 5 x_{4}-x_{5} x4−x5 替换 x 3 , x_{3}, x3, 其中 x 4 , x 5 ≥ 0 x_{4}, x_{5} \geq 0 x4,x5≥0 ;
- 在第一个约束不等式左端加入松他变量 x 6 x_{6} x6 ;
- 在第二个约束不等式左端減去剩余变量 x 7 x_7 x7 ;
- 令z’= -z,将求min z 改为求max z’.
得到标准型:
max z ′ = x 1 − 2 x 2 + 3 ( x 4 − x 5 ) + 0 x 6 + 0 x 7 { x 1 + x 2 + ( x 4 − x 5 ) + x 6 = 7 x 1 − x 2 + ( x 4 − x 5 ) − x 7 = 2 − 3 x 1 + x 2 + 2 ( x 4 − x 5 ) = 5 x 1 , x 2 , x 4 , x 5 , x 6 , x 7 ≥ 0 \begin{aligned} &\max z^{\prime}=x_{1}-2 x_{2}+3\left(x_{4}-x_{5}\right)+0 x_{6}+0 x_{7}\\ &\left\{\begin{array}{cc} \quad \quad \quad x_{1}+x_{2}+\quad \left(x_{4}-x_{5}\right)+x_{6}& \quad \quad =7 \\ \quad x_{1}-x_{2}+\quad \left(x_{4}-x_{5}\right) & -x_{7}=2 \\ -3 x_{1}+x_{2}+2\left(x_{4}- x_5\right) & \quad \quad =5 \\ x_{1}, x_{2}, x_{4}, x_{5}, x_{6}, x_{7} \geq 0 \end{array}\right. \end{aligned} maxz′=x1−2x2+3(x4−x5)+0x6+0x7⎩⎪⎪⎨⎪⎪⎧x1+x2+(x4−x5)+x6x1−x2+(x4−x5)−3x1+x2+2(x4−x5)x1,x2,x4,x5,x6,x7≥0=7−x7=2=5
线性规划问题的解概念
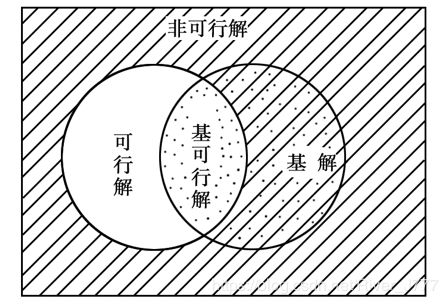
- 可行解
满足所有约束条件的解称为可行解,可行解中使目标函数达到最大值的解为最优解. - 基
B B B 是系数矩阵A( R ( A ) = m R(A)=m R(A)=m)中的 m × m m\times m m×m阶非奇异子矩阵 ( B ∣ ≠ 0 ) (\mathrm{B} | \neq 0) (B∣=0) 称B为线性规划问题的基。 B = ( a 11 a 12 ⋯ a 1 m a 21 a 22 ⋯ a 2 m ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) = ( P 1 , P 2 , ⋯ P m ) B=\left(\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n}\end{array}\right)=\left(P_{1}, P_{2}, \cdots P_{m}\right) B=⎝⎜⎜⎜⎛a11a21⋮am1a12a22⋮am2⋯⋯⋯a1ma2m⋮amn⎠⎟⎟⎟⎞=(P1,P2,⋯Pm)
P j ( j = 1 , 2 , ⋯ m ) \mathrm{P}_{\mathrm{j}}(j=1,2, \cdots m) Pj(j=1,2,⋯m) 为基向量
x j ( j = 1 , 2 , ⋯ m ) \mathbf{x}_{\mathrm{j}}(j=1,2, \cdots m) xj(j=1,2,⋯m) 为基变量。 - 基可行解
满足非负条件 x ≥ 0 x\geq0 x≥0的基解,称为基可行解. 基可行解的非零分量的数目不大于m,并且都是非负的。
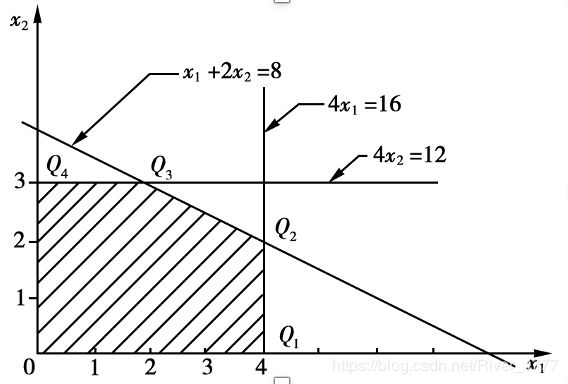
上图中 0 , Q 1 , , Q 2 , Q 3 , Q 4 0,Q_1,,Q_2,Q_3,Q_4 0,Q1,,Q2,Q3,Q4都是基可行解. - 可行基
对应于基可行解的基,称为可行基。 约束方程组 A x = b Ax=b Ax=b具有的基解的数目最多是 C n m C_{n}^{m} Cnm 个,一般 基可行解的数目要小于基解的数目.