数学建模 送货问题

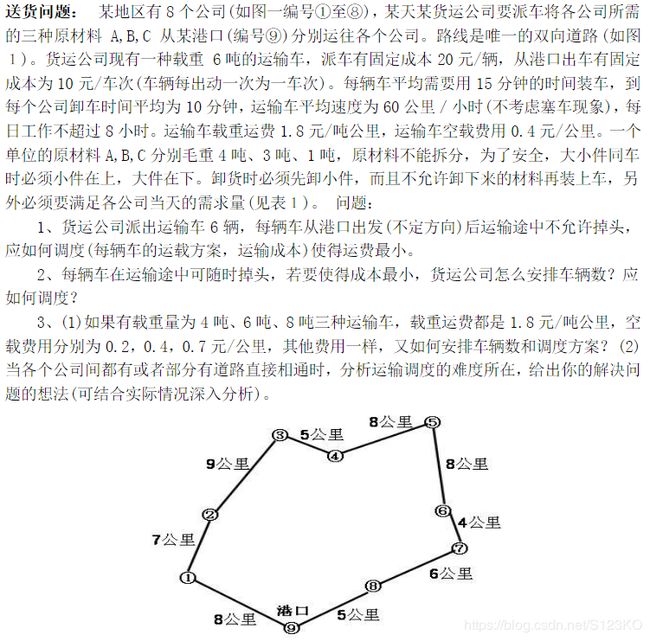
送货问题

摘要

本文主要讨论的是送货问题，根据各公司对材料的需求和运输路线图，建立了线性规划模型，对货运公司的出车安排进行了分析和优化，得出运费最小的调度方案。

问题一中每辆车从港口出发，运输途中不能掉头，为使运输费用最小，要使在一定的车辆数下，既满足各公司的需求，又要尽量减小出车次数。故以最小出车数为目标函数，建立线性规划模型。通过工具可以得出最小的出车次数为27次。又因为运输方向不定，出车方向可为顺时针和逆时针方向，通过解出的装车方式，得出结果。

问题二每辆车从港口出发，允许运输途中掉头，类似于问题一的求解方法，只需要满足空车的的运输路程最短。

 

问题重述

符号说明

X1:一车装1单位的A材料，2单位的C材料

X2:一车装6单位的C材料

X3:一车装2单位的B材料

X4:一车装1单位的B材料，3单位的C材料

X5：一车装1单位的A材料，1单位的C材料

X6:一车装1单位的A材料

S:最小运输次数

P：为0时顺时针运输，为1时逆时针运输

Xij：第i次运输材料j的单位数

Yij：第i次运输j到达目的地所走的路程

a：各公司对A的总需求量

b：各公司对B的总需求量

c：各公司对C的总需求量

 

模型假设

1. 每次装载时发挥最大装载能力
2. 每天每辆车可以达到最大的作业时间
3. 在人力和运输费用最少时，考虑最少运输费用

 

问题分析

本题要求从一个港口向八个地点发货，每辆车日工作时间不超过8小时，运输车的平均速度为60公里每小时，一共有6辆车从港口出发，中途不得掉头，每辆车需要15分钟的装车时间和到每个公司10的卸货时间。

问题一假设一辆车在全程只装一次，也只卸一次，即用时最短，会花上85分钟，又因为一辆车工作时间不能超过8h，故一辆车最多跑5次，六辆车共跑30次，通过公式与工具运算可以得出最少需要运送27次，其中需要9次装2单位的B，8次装1单位的A和2单位的 C，10次装1单位的A和一单位的C。

问题二可以类比与问题一，解题思路一致，要求最小成本，合理安排好运输次序，先卸小件再卸大件，并保证空车的路程最短，即可实现。

 

 

 

模型建立

总共有6辆车，若一辆车在全程只装1次车，只卸一次车，那么它所花费的时间最少，即会花85分钟，而一辆车的工作时间不能超过8h，所以一辆车最多能跑5趟，六辆车总共能跑30趟，而每俩车每次只能运6吨的货物，所以每辆车可能运输1单位的A和2单位的C（X1），6单位的C(X2),2单位的B(X3),1单位的B和3单位的C（X4）

所以s(min)=X1+X2+X3+X4

X1=18 

2*X3+X4=18 

2*X1+6*X2+3*X4>=26

此时的模型会导致多运输C，所以可以是后来每辆车不装满，即每辆车运输1单位的A和一单位的C（X5），一单位的A（X6）

所以s(min)= X1+X2+X3+X4+X5+X6

X1+X5+X6=18

2*X=3+X4=18 

2*X1+3*X4+6*X2+X5=26

X1+X2+X3+X4+X5+X6<=30

 

模型建立：

若设Xi1为第i次运输材料A的单位数；Xi2为第i次运输材料B的单位数;Xi3为第i次运输材料C的单位数，Yi1为第i次运输A到达目的地所走的路程；Yi2为第i次运输B到达目的地所走的路程；Yi3为第i次运输C到达目的地所走的路程，Zij为第i次运输j到达目的地的单位成本。建立最小运费的模型：

Mi=1mj=1nZijXijYij

每辆车的容量：

4Xi1+3Xi2+Xi3<=6

各公司对A，B，C的总需求：

i=1mXi1=a

i=1mXi2=b

i=1mXi3=c

 

问题一模型建立

满足条件后最少需要运输27次，其中需要9次装2单位的B，8次装1单位的A和2单位的 C，10次装1单位的A和一单位的C。

装9次2单位的B，按照奇偶数的进行分配。其中可以按顺时针方向向②地运输2车2单位的的B，然后逆时针向⑧地运输1车2单位的的B，向⑦地运输1车2单位的B，向⑥地运输2车2单位的B，向⑤地运输1车的2单位的B，然后顺时针分别向①地运输1单位的B，向②地运输1单位的B，逆时针向⑧地运输1单位的B，向④地运输1单位的B（具体表述如下表）

 

（0代表从顺时针方向开始出发，1代表从逆时针方向开始出发）

方向		① 1	② 5	③0	④ 1	⑤ 2	⑥ 4	⑦ 2	⑧ 3
0	① 1	(1*2B)/2	(1*2B)/2
0	② 5		2*2B
	③ 0
1	④ 1				(1*2B)/2				(1*2B)/2
1	⑤ 2					1*2B
1	⑥ 4						2*2B
1	⑦ 2							1*2B
1	⑧ 3								1*2B
载重总运费		86.4	361.8		140.4	248.4	324	118.8	108

 

载货时的运费=86.4+405+167.4+248.4+324+118.8+108=1383.3

运输车为空车的运费=(45*3+55+49+45*2+37+29)*0.4=158

总运费=1383.3+158=1541.3

 

方向		① 4 5	② 1 2	③ 2 4	④ 3 2	⑤ 1 4	⑥ 0 3	⑦ 2 5	⑧ 5 1	总运费	时间
0	1A2C	(1,2)								107.2
0	1A2C		(1,2)							180
0	1A2C			(1,2)						273.6
0	1A2C			(1,2)						273.6
1	1A2C							(1,2)		138.4
1	1A2C							(1,2)		138.4
1	1A2C					(1,0)	(0,1)	(0,1)		227.2
1	1A2C				(1,0)		(0,2)			288.8
0	1A1C	(1,1)								94
0	1A1C	(1,1)								94
0	1A1C	(1,1)								94
1	1A1C				(1,0)	(0,1)				276.2
1	1A1C				(1,0)	(0,1)				276.2
0	1A1C				(0,1)				(1,0)	450.2
0	1A1C				(0,1)				(1,0)	450.2
0	1A1C					(0,1)			(1,0)	464.6
0	1A1C					(0,1)			(1,0)	464.6
1	1A1C								(1,1)	67

 

运输A和C 的总费用=4358.2

所以 运输A,B,C的全部费用=4358.2+1541.3+120+270=6289.5

 

问题二模型建立

因为运输过程中运输车可以掉头，因此只需要求空车时路程最短，具体模型如下：

 

（0代表从顺时针方向开始出发，1代表从逆时针方向开始出发）

方向		① 1	② 5	③0	④ 1	⑤ 2	⑥ 4	⑦ 2	⑧ 3
0	① 1	(1*2B)/2	(1*2B)/2
0	② 5		2*2B
	③ 0
1	④ 1				(1*2B)/2				(1*2B)/2
1	⑤ 2					1*2B
1	⑥ 4						2*2B
1	⑦ 2							1*2B
1	⑧ 3								1*2B
载重总运费		86.4	405		167.4	248.4	324	118.8	108

 

载货时的运费=86.4+405+167.4+248.4+324+118.8+108=1383.3

运输车为空车的运费=(15*3+5+11+15*2+23+29)*0.4=57.2

总运费=1383.3+57.2=1440.5

 

方向		① 4 5	② 1 2	③ 2 4	④ 3 2	⑤ 1 4	⑥ 0 3	⑦ 2 5	⑧ 5 1	总运费	时间
0	1A2C	(1,2)								89.6
0	1A2C		(1,2)							168
0	1A2C			(1,2)						268.8
0	1A2C			(1,2)						268.8
1	1A2C							(1,2)		123.2
1	1A2C							(1,2)		123.2
1	1A2C							(0,1)	(1,1)	153.2
1	1A2C					(1,2)				257.6
0	1A1C	(1,1)								75.2
0	1A1C	(1,1)								75.2
0	1A1C	(1,1)								75.2
1	1A1C						(0,1)		(1,0)	209
1	1A1C						(0,1)		(1,0)	209
1	1A1C						(0,1)		(1,0)	209
1	1A1C					(0,1)			(1,0)	338.6
1	1A1C				(1,0)	(0,1)				276.2
0	1A1C				(1,1)					272.6
0	1A1C				(1,1)					272.6

 

运输A和C 的总费用=3645

所以 运输A,B,C的全部费用=3645+1440.5+120+270=5475.5

 

模型的评价与修正

本题通过线性规划的优化求解方法，求出最少运输次数的模型，根据此模型合理安排车辆的运输情况，以使成本最少。运用此模型可以合理安排生活中的一些运输问题，可靠性和实践性较强，但模型中的一些假设虽有理，但与实际生活还有一些差距，应该在实际应用时，做出其他的预案。