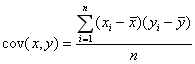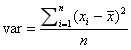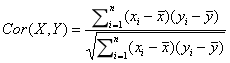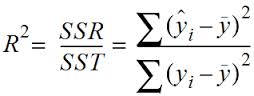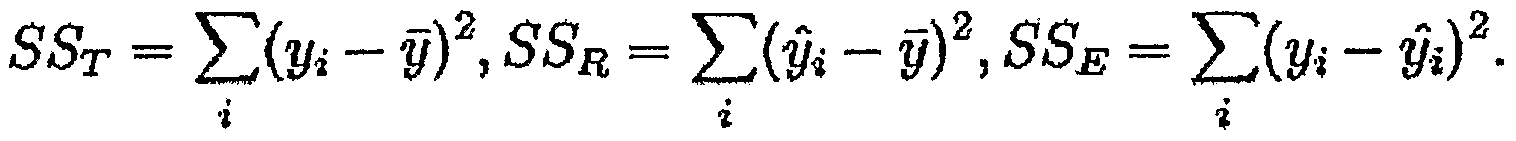机器学习-回归中的相关度和R平方值

1. 皮尔逊相关系数(Pearson Correlation Coefficient)

     1.1 衡量两个值线性相关强度的量

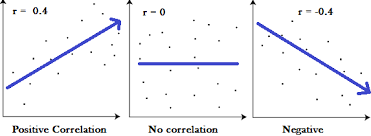
     1.2 取值范围[-1, 1]

            正相关：>0, 负相关：<0, 无相关：=0

      1.3 要理解Pearson相关系数，首先要理解协方差（Covariance），协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下： 

                            

 

             方差：

                            

             Pearson相关系数公式如下：

                            

                           

            注意：有了协方差，为什么还使用皮尔逊相关系数？虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度，例如，现在二维空间中分布着一些数据，我们想知道数据点坐标X轴和Y轴的相关程度，如果X与Y的相关程度较小但是数据分布的比较离散，这样会导致求出的协方差值较大，用这个值来度量相关程度是不合理的。 
           为了更好的度量两个随机变量的相关程度，引入了Pearson相关系数，其在协方差的基础上除以了两个随机变量的标准.

2. 计算方法举例：

     x      y

     1     10

     3     12

     8     24

     7     21

     9     34

    在Excel中计算：

3. 其他例子

    

4. R平方值

    4.1 定义：决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。

                    也就是说，对于已经建模的模型，多大程度上可以解释数据

   4.2 描述：如R平方为0.8，则表示回归关系可以解释因变量80%的变异。换句话说，如果我们控制自变量不变，则因变量的变异程度会减少80%。

   4.3 简单线性回归：R^2 = r * r (r为皮尔逊相关系数)

         多元线性回归：

                      

                                        

 

        R平方也有局限性：R平方随着自变量的增加会变大，R平方和样本量是有关系的。因此，我们要对R平方进行修正。修正方法：

                                                

        实际中一般会选择修正后的R平方值对线性回归模型对拟合度进行评判

 Python实现：

# -*- coding:utf-8 -*-

import numpy as np
from astropy.units import Ybarn
import math

#相关度
def computeCorrelation(X, Y):
    xBar = np.mean(X)
    yBar = np.mean(Y)
    SSR = 0
    varX = 0
    varY = 0
    for i in range(0, len(X)):
        diffXXbar = X[i] - xBar
        diffYYbar = Y[i] - yBar
        SSR += (diffXXbar * diffYYbar)
        varX += diffXXbar**2
        varY += diffYYbar**2
    SST = math.sqrt(varX * varY)
    return SSR / SST

#测试
testX = [1, 3, 8, 7, 9]
testY = [10, 12, 24, 21, 34]

# print("相关度r:", computeCorrelation(testX, testY))
#相关度r: 0.940310076545

#R平方
#简单线性回归：
# print("r^2:", str(computeCorrelation(testX, testY)**2))
#r^2: 0.884183040052

#多个x自变量时：
def polyfit(x, y, degree): #degree自变量x次数
    result = {}
    coeffs = np.polyfit(x, y, degree)
    result['polynomial'] = coeffs.tolist()

    p = np.poly1d(coeffs)
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat - ybar)**2)
    sstot = np.sum((y - ybar)**2)
    result['determination'] = ssreg / sstot

    return  result

#测试
print(polyfit(testX, testY, 1)["determination"])
#r^2:0.884183040052

　　

转载于:https://www.cnblogs.com/lyywj170403/p/10460238.html