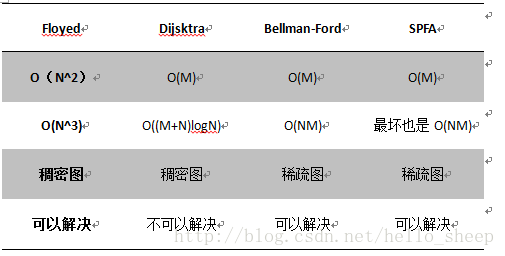
【图论】【最短路径模板+邻接表】【Floyed+Dijsktra+Bellman-Ford+SPFA】【最短路算法对比分析】

ACM模板

【最短路】:最短路是不包含回路的简单路径。

【Floyed】

多源最短路，即要求求出图中每两个顶点之间的最短路。虽然Floyed的复杂度是O（n^3）,但是4行却简单很多，本质上是动态规划算法。
思想：从i号顶点到j号顶点只经过前k号顶点的最短路径。

#define INF 999999

int Floyd()
{//初始化n个顶点 
    for(i = 1; i <= n; i ++)
        for(j = 1; j <= n; j ++)
            if(i == j)
                e[i][j] = INF;
            else
                e[i][j] = 0;
    for(k = 1; k <= n; k ++)//Floyd-Warshall算法核心语句 
        for(i = 1; i <= n; i ++)
            for(j = 1; j <= n; j ++)
                if(e[i][j] > e[i][k]+e[k][j])
                    e[i][j] = e[i][k]+e[k][j];
}

【Dijkstra】

Dijkstra算法适合不含负权边的单源最短路（单源最短路是指从源点到其余各个顶点的最短路径）。
思想：每次找到离源点最近的一个顶点，然后以该顶点为中心进行拓展，最终得到源点到其余所有点的最短路径

#define inf 99999999//用inf存储一个我们认为是正无穷的值
//读入n,m。n表示顶点个数,m表示边的条数 
memset(book,0,sizeof(book));
for(i = 1; i <= n; i ++)
    for(j = 1; j <= n; j ++)
        if(i == j)
            e[i][j] = 0;
        else
            e[i][j] = 1;

for(i = 1; i <= m; i ++)
{
    scanf("%d%d%d",&t1,&t2,&t3);
    e[t1][t2] = t3;
}
//初始化dis数组，1号顶点到其余各个顶点的初始路程 
for(i = 1; i <= n; i ++)
    dis[i] = e[1][i];
book[1] = 1;
//Dijkstra算法核心语句 
for(i = 1; i <= n-1; i ++)
{
    min = inf;
    //找到离1号顶点最近的顶点 
    for(j = 1; j <= n; j ++)
    {
        if(!book[j]&&dis[j]1;
for(j = 1; j <= n; j ++)
{
    if(dis[j] > dis[u] + e[u][j])
        dis[j] = dis[u] + e[u][j];
}
for(i = 1; i <= n; i ++)//输出
    printf("%d ",dis[i]);
printf("\n");

【Bellman-Ford】

Bellman-Ford算法能解决存在负权边的单源点最短路径问题。可以检测一个图是否存在负权回路：如果在进行了n-1轮松弛后，仍然可以继续成功松弛，说明存在负权边。

#define inf 99999999
struct node{
    int from,to,w;
};
node edge[100];
bool Ford()
{
    for(i = 1; i <= n; i ++)
        dis[i] = inf;
    dis[1] = 0;
    for(i = 1; i <= n; i ++)
    {
        flag = false;
        for(j = 1; j <= m; j ++)
        {
            x = edge[i].from ;
            y = edge[i].to ;
            z = edge[i].w ;
            if(dis[y] > dis[x] + z)
            {
                dis[y] = dis[x] + z;
                flag = true;
            }
        }
        if(!flag)
            break;
        //如果更新到n遍，还能够继续更新dis数组，说明存在负权环 
        if(flag&&i == n) 
            return false;//返回false表示这个图存在负权环 
    }
    return true;//返回true表示求最短路成功 
}

【SPFA】

SPFA是Bellman-Ford算法的队列实现。SPFA加入了一个队列保存信息。用一个数组book来标记一个顶点是否已经加入了队列。
队列优化：只对最短路估计值发生了变化的顶点的所有出边执行松弛操作
求源点到终点的最短路

struct node{
    int to;
    int w;
    int next;
}Edge[maxn];
void Add_edge(int u,int to,int w)
{
    Edge[cnt].to = to;//被指向的点 
    Edge[cnt].w = w;//边权 
    Edge[cnt].next = head[u];//记录cnt的下一条出边 
    head[u] = cnt++;//顶点u指向的第一条边 
    return;
}
void spfa()
{
    queue<int>q;
    for(i = 0; i <= n; i ++)//初始化dis数组，源点start到其余各点的初始距离 
        dis[i] = inf;
    dis[start] = 0; 
    book[start] = 1;//源点已经入队 
    q.push(start);//源点入队 
    while(!q.empty())
    {
        nowq = q.front();
        q.pop();
        book[nowq] = 0;//和广度优先搜索的不同之处，当一个顶点的最短路程估计值变小后，需要再次对其所有出边进行松弛 
        for(i = head[nowq]; i != -1; i = Edge[i].next)//遍历松弛以nowq为起点的所有出边 
        {
            to = Edge[i].to;
            w = Edge[i].w;
            if(dis[to] > dis[nowq]+ Edge[i].w ) //使得源点到to的距离变短 
            {
                dis[to] = dis[nowq]+Edge[i].w;
                if(!book[to])//同一顶点多次出现在队列中是毫无意义的，所以需要判重 
                {
                    book[to] = 1;//标记为已经入队 
                    q.push(to);
                }
            }
        }
    }
    return ;
}
main()
{
    memset(head,-1,sizeof(head));//head[i]存储以i为顶点的第一条边 
    memset(book,0,sizeof(book));//初始化book数组，一开始都没有加入队列 
    cnt = 0;//记录边数 
    Add_edge(u,v,w);//单向则只加入一次 
    Add_edge(v,u,w);
    spfa();
    printf(dis[end]);//输出源点到终点的最短距离 
}

判断负权回路

void addedge(int a,int b,int c)
{
    e[num].to = b;
    e[num].w = c;
    e[num].next = first[a];//邻接表存图 
    first[a] = num++;
}//dis和fisrt在主函数中全部初始化为-1 
bool spfa(int s)
{
    int used[N];//用来记录一个顶点入队次数 
    bool book[N];//标记该点是否在队列中 
    int head,tail,i,to,now;
    queue<int>Q;
    memset(used,0,sizeof(used));
    memset(book,false,sizeof(book));
    Q.push(s); 
    book[s] = true;
    used[s]++;
    dis[s] = 0;
    while(!Q.empty())
    {
        now = Q.front() ;
        Q.pop() ;
        book[now] = false;
        for(i = first[now];i!=-1;i = e[i].next)
        {
            to = e[i].to ;
            if(dis[to]>dis[now]+e[i].w)
            {
                dis[to] = dis[now] + e[i].w ;
                used[to]++;
                if(used[to]>=n)//一个点使用超过n，一定存在负环 
                    return false;
                if(!book[to])//如果顶点不在队列中，入队 
                {
                    book[to] = true;//标记为已经入队 
                    Q.push(to) ;
                }
            }
        }
    } 
    return true;//不存在负权边 
}

【邻接表】

【邻接表邻接矩阵时间复杂度和空间复杂度分析】
假设图中有n个顶点,m条边
时间复杂度：邻接表直接存储边的信息，有向图是O(M),无向图是O(2*M)。邻接矩阵间接存储边的信息，复杂度是O(N*N)
空间复杂度：邻接表：O(N+M)或O（N+2*M）,邻接矩阵：O(N*N)

//数组实现邻接表  共m条边

for(i = 1; i <= m; i ++)
{
    scanf("%d%d%d",&u[i],&v[i],&w[i]);
    next[i] = first[u[i]];
    first[u[i]] = i;
 } 

for(i = 1;i <= n; i ++)
{
    k = first[1];
    while(k!=-1)
    {
        printf("%d %d %d\n",u[k],v[k],w[k]);
        k = next[k];
    } 
}