材料力学知识点总结(20200723更新)

2020年春季学期学习了材料力学（ AS31204），作为一名大二结束分流到工程力学的力学狗，偶尔写写总结，记一下原理，总是有好处的，课程教材采用的是张少实，王春香教授主编的新版材料力学第三版，ISBN 978-7-111-58650-0

绪论

材料力学研究任务

1. 构件应有足够的强度(strength)
2. 构件应有足够的刚度(stiffness)
3. 构件应有足够的稳定性(stability)

变形固体的基本假设

1. 连续性假设
2. 均匀性假设
3. 各向同性假设
4. 小变形

变形固体基本假设非常重要，具体参考文章：李宏德.谈材力中变形固体的基本假设[J].河南机专学报,1997(03):18-19+17.

外力

外力(external force)包括载荷与支反力，按其作用方式可分为体积力和表面力。

材料的力学性能与应力应变分析

内力、应力与应变

材料的力学性能与基本实验

应力应变状态分析

各项同性材料的胡克定律

各项同性材料弹性常数关系

材料的基本变形

轴向拉压、扭转

弯曲

弯曲变形

梁在简单载荷下的变形

序号	梁的简图	挠曲线方程	端截面转角	最大挠度
1		$$v=\frac{M_e{x}^2}{2EI}$$	$${\theta }_B=\frac{M_{e}l}{EI}$$	$$v_B=\frac{M_e{l}^2}{2EI}$$
2			$${\theta }_B=\frac{M_{e}a}{EI}$$	$$v_B=\frac{M_{e}a}{EI}\left(l-\frac{a}{2}\right)$$
3		$$y=-\frac{F{x}^2}{6EI}(3a-x)$$	$${\theta }_B=-\frac{F{l}^2}{EI}$$	$$v_B=-\frac{F{l}^3}{6EI}$$
4		$$\{\begin{array}{c}y=-\frac{F{x}^2}{6EI}(3a-x),0⩽x⩽a\\ \\ y=-\frac{F{a}^2}{6EI}(3x-a),a⩽x⩽l\end{array}$$	$${\theta }_B=-\frac{F{a}^2}{EI}$$	$$v_B=-\frac{F{a}^2}{6EI}(3l-a)$$
5
6
7
8
9
10
11

组合变形

斜弯曲

$${\sigma }_x=-\frac{M_z{y}_k}{I_z}-\frac{M_y{z}_k}{I_y}$$

偏心拉压

弯扭组合

材料失效与强度理论

强度理论

常用的强度理论总共有以下四种，但是强度理论不止以下四种，还有摩尔强度理论等。

强度理论	应用材料	形式
第一强度理论（最大拉应力理论）	脆性材料	$${\sigma }_{r_1}={\sigma }_1$$
第二强度理论（最大拉应变理论）	脆性材料	$${\sigma }_{r_2}={\sigma }_1-\nu ({\sigma }_2+{\sigma }_3)$$
第三强度理论（最大切应力理论）	塑性材料	$${\sigma }_{r_3}={\sigma }_1-{\sigma }_3$$
第四强度理论（形变应变能理论）	塑性材料	$${\sigma }_{r_4}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2\right]}$$

强度条件

许用应力$$\left[\sigma \right]=\frac{{\sigma }_s}{n}$$
$n$为安全因数
强度条件$${\sigma }_{\max }⩽\left[\sigma \right]$$
刚度条件$${\Delta }_{\max }⩽\left[\Delta \right]$$

强度计算&结构设计

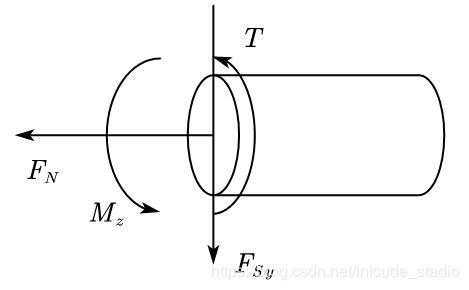
强度计算的核心在于确定危险点，通常确定危险点的方式为：画$F_N-x,T-x,F_{s_y}-x,M_z-x$图。进而寻找${\sigma }_{x\max }$，对其进行强度校核。
结构设计要求危险点应力小于许用应力，本质亦是强度校核。

轴向拉伸

强度校核：
$${\sigma }_{\max }=\frac{F}{A}⩽\left[\sigma \right]$$
结构设计：

• 圆轴：$$d⩾\sqrt{\frac{4F_N}{\pi \left[\sigma \right]}}=\sqrt{\frac{1.273F_N}{\left[\sigma \right]}}$$
• 正方形轴：
  $$a⩾\sqrt{\frac{F_N}{\left[\sigma \right]}}$$

扭转

小变形情况下，扭转主要产生切应力。
强度条件：
$${\tau }_1⩽\left[\sigma \right],{\tau }_2⩽\frac{1}{1+\nu }\left[\sigma \right],{\tau }_3⩽\frac{1}{\sqrt{2}}\left[\sigma \right],{\tau }_4⩽\frac{1}{\sqrt{3}}\left[\sigma \right]$$
刚度条件：
$${\phi }_{\max }=\frac{180°}{\pi }{\left(\frac{T}{G{I}_p}\right)}_{\max }⩽\left[\phi \right]$$
结构设计：
设$\tau ⩽A\left[\sigma \right],{\tau }_{\max }=\frac{T_{\max }}{W_t}$。

• 实心圆轴
  强度设计：
  $$d_1⩾\sqrt[3]{\frac{16T_{\max }}{A\pi \left[\sigma \right]}}=\sqrt[3]{\frac{5.093T_{\max }}{A\left[\sigma \right]}}$$
  刚度设计：
  $$d_2⩾\sqrt[4]{\frac{32T_{\max }\times 180°}{G{\pi }^2\left[\phi \right]}}=\sqrt[4]{\frac{583.6T_{\max }}{G\left[\phi \right]}}$$
• 空心圆轴
  强度设计：$D_1⩾\sqrt[3]{\frac{5.093T_{\max }}{A\left[\sigma \right]\left(1-{\alpha }^4\right)}}$，刚度设计：$D_2⩾\sqrt[4]{\frac{583.6T_{\max }}{G\left[\phi \right]\left(1-{\alpha }^4\right)}}$。

组合变形

塑性材料组合内力：
$${\sigma }_{r_3}=\sqrt{{\sigma }_x^2+4{\tau }_{xy}^2}$$
$${\sigma }_{r_3}=\sqrt{{\sigma }_x^2+3{\tau }_{xy}^2}$$
弯扭组合：
$${\sigma }_{r_3}=\frac{1}{W_t}\sqrt{M^2+T^2}$$
$${\sigma }_{r_4}=\frac{1}{W_t}\sqrt{M^2+\frac{3}{4}{T}^2}$$

压杆稳定

能量方法

单位载荷法

$$1\cdot \Delta =\int \left(\frac{F_N\cdot \overline{F_N}}{EA}+\frac{T\cdot \overline{T}}{G{I}_p}+\frac{M_z\cdot \overline{M_z}}{E{I}_z}+\frac{k{F}_{s_y}\cdot \overline{F_{s_y}}}{GA}\right)\mathrm{d}x$$

图乘法

$$\Delta =\frac{{\Omega }_{F_N}{\omega }_{F_N}}{EA}+\frac{{\Omega }_T{\omega }_T}{G{I}_p}+\frac{{\Omega }_{M_z}{\omega }_{M_z}}{E{I}_z}+\frac{k{\Omega }_{F_{s_y}}{\omega }_{F_{s_y}}}{GA}$$

超静定结构

一次超静定

力法方程$${\delta }_{11}{X}_1+{\Delta }_{1F}=0$$

二次超静定

力法方程
$$\left(\begin{array}{cc}{\delta }_{11}& {\delta }_{12}\\ {\delta }_{21}& {\delta }_{22}\end{array}\right)\left(\begin{array}{c}{X}_1\\ X_2\end{array}\right)+\left(\begin{array}{c}{\Delta }_{1F}\\ {\Delta }_{2F}\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

对称载荷

对称于结构的对称轴，对称截面上，反对称内力为零；
反对称于结构的对称轴，对称截面上，对称内力为零。
结构的对称性能够有效地简化超静定次数，提高解题效率。

超静定解题步骤（一次超静定）

• step1：判断结构对称性，确定超静定次数，列力法方程：
  卸载所求点处的支座，并施加约束反力$X_1$（求支座反力类型），设单位力$\overline{F}=1$；
  卸载固定端，改为固定铰支座，并施加约束力偶$X_1$，设单位力矩$\overline{M}=1$（求力偶矩类型）；
  断开某杆，设杆内轴力为$X_1$，设单位力$\overline{F}=1$（求杆件轴力型）；
• step2：做原载荷作用下的$F_N-x,T-x,M_z-x$图；
• step3：忽略全部外载，做单位力（矩）作用下的$\overline{F_N}-x,\overline{T}-x,\overline{M_z}-x$图；
• step4：由摩尔积分或图乘法，求出${\delta }_{11},{\Delta }_{1F}$；
• step5：代入力法方程，解出未知力$X_1$。
  二次超静定也采用这个步骤，只不过约束反力、单位力均增加。此时应当合理采用对称性，化简单位力（矩）自乘情况。

弯杆常用积分

$$\int {\sin }^{3}x=\frac{1}{3}{\cos }^{3}x-\cos x+C$$
$$\int {\cos }^{3}x=-\frac{1}{3}{\sin }^{3}x+\sin x+C$$
$$\int {\sin }^{2}x=-\frac{1}{4}\sin 2x+\frac{1}{2}x+C$$
$$\int {\cos }^{2}x=\frac{1}{4}\sin 2x+\frac{1}{2}x+C$$

更新日志

• 0720：2020春季学期材料力学A期末考试终于考完了，感觉期末考试题比以往简单的多，由于个人复习爱好（习惯性的大总结），感觉考试总结总结的挺好，遂产生做博客的想法。
• 0721：更新：梁在简单载荷下的变形/强度理论/超静定。
• 0722：更新：超静定/强度理论。
• 0723：更新：组合变形。