字符串匹配就是查找子串是否在主串中,或者在主串的哪个位置上。一般而言,使用暴力破解,将子串与主串一一对比就可以找到结果,但是这样的复杂程度太高,比如主串是aaaaaaaaaaaac,子串是aaaac,过程就是主串的第一个a和子串的第一个a对比,相同,对比第二个,一直到主串的第五个a和子串最后的c对比的时候,发现无法匹配,那么之后将主串的第二个a和子串的第一个a重新对比,相同,再和上面的过程一样,对比第二个,一直到主串的a和子串最后的c对比,发现不同。一直对比到主串的最后部分,才发现相同。
问题所在
暴力破解最大的问题是重复对比,因为子串前面是四个a,主串前面也都是a,那么在对比的时候,发现字符串不匹配,进入下一轮匹配的时候,能否将前面那些子串中a与主串中a的匹配过程省略掉呢?意思就是发现主串的第五个字符a和子串第五个字符c不匹配的时候,子串向右滑动一格,之后将主串第五个字符a和子串的第四个字符a进行匹配,匹配成功后,再将主串的第六个字符a与子串的第五个字符c进行对比,这样一来子串前面三个字符就不用与主串进行对比了,因为它们都是一样的,KMP就是利用部分匹配的结果将字符串匹配尽量向右滑动对比,这样减少了对比的次数。下面图来表示整个过程。

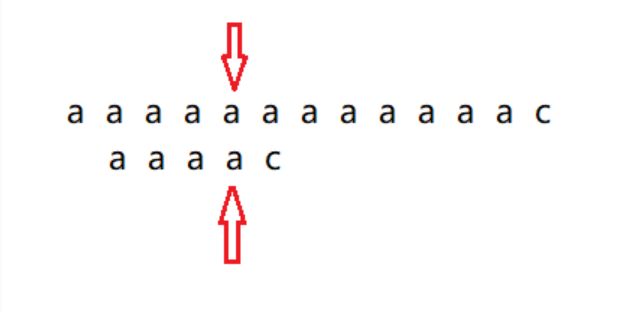

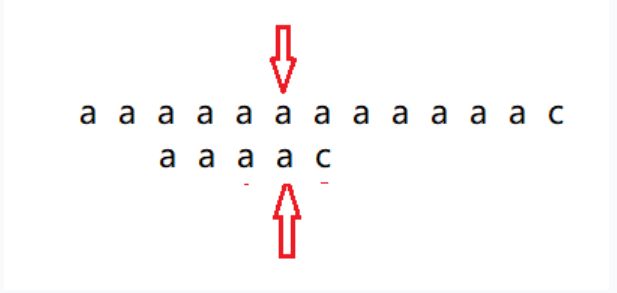
实现思路
上面已经说明了整体的思路,并且将思路用图表现出来。关键在于如何实现,如何知道这个子串在下一轮匹配开始的时候要滑动到哪个位置上?因为主串和子串匹配完成的部分字符串都是一样的,那么只需要从子串本身出发。找出子串中前缀和后缀哪些是一样的。之前的aaaaaaaaaaaac中,子串aaaac的匹配,因为子串与主串的匹配是一一匹配的,先将子串aaaac分成五个小子串,分别是a,aa,aaa,aaaa,aaaac。然后再看每个小子串最长的相同前后缀是多少。

这就是KMP算法的第一步,得出子串的前缀长度。
有了子串的前缀长度了,下面就是根据子串的前缀长度得到子串的滑动位置,这是因为如果我们发现子串中第五个字符c和主串中第五个字符a不相同的时候,之后找到前面的aaaa子串前后缀最长相同长度是3,说明aaaa前三个字符与最后三个字符是一样,那么它只需要再往后移动一格,再将子串第四个字符与主串第五个字符进行比较,本质就是子串比较的位置在第五个字符c上的时候,移动到的位置就是子串的第四个字符a,也就是3(从0开始)。如果第一个小子串a就不匹配的话,那么就得将之移动,这里不能是0,应该是-1,也就是子串最前面的位置。

这就是实现的第二步,得到子串的滑动位置。
有了上面的结果,就能将子串与主串进行匹配操作了,也就是最后一步,主串与子串的匹配。

有了上面的滑动位置表了,那么发生图中不匹配的情况时,直接找到滑动位置表,找到aaaac的位置是3,那么就将3这个位置滑动过来,将之与主串进行匹配对比。

这样就能很快得出匹配结果了。
代码实现
上面的算法思想基本诠释了算法的过程,但是在代码实现中,需要对其中的步骤进行优化处理。
在第一步得出子串的前缀长度,对于每一个小子串,我们并不需要每个都重新对比,这时需要看前面小子串的情况,比如在计算aaaa的时候,我们可以看aaa的情况,aaa的长度是2,那么只需要比较aaaa中第三个字符和最后一个字符是否相同就行,因为aaa长度为2已经保证了aaaa前三个的前后缀是一样的,只要比较新加入的字符是否相同即可。如果相同,那么只需要将2+1=3就可以得到结果,但是如果不相同,不能直接将之赋成0,因为可能存在相同子串。举一个典型的例子,比如子串是abaabab,

最后一个小子串是abaabab,在求这个小子串长度的时候,需要先看abaaba,可以看到它的长度是3,整体可以分为

public void getPrefix(String child_str,int[] prefix_table,int child_str_length) {
prefix_table[0] = 0;
char[] child_chars = child_str.toCharArray();
int index = 1;
int compared_index = 0;
while(index < child_str_length) {
if(child_chars[index] == child_chars[compared_index]) {
prefix_table[index++] = ++compared_index;
}else {
if(compared_index > 0) {
// 这一步是重点,整个函数中最精髓的地方,个人理解是等号的传递性
// 这边好好理解
compared_index = prefix_table[compared_index - 1];
}else {
prefix_table[index++] = 0;
}
}
}
}
第二步就是移动,这里在代码中的实现和上述的表述是基本一致的。
private void movePrefix(int[] prefix,int child_str_length) {
for(int index = child_str_length - 1;index > 0; index--) {
prefix[index] = prefix[index - 1];
}
prefix[0] = -1;
}
第三步就是进行字符串匹配,如果字符串匹配,那么继续比较下一个字符,如果不同,那么移动子串位置,这里有一个特殊的情况,如果移动到-1,之前我们说-1就是子串前面的位置,本质上就是比较下一个字符,如果子串已经比较完成并且都相同,那么就是找到了一个子串。
public void findStr(String main_str, String child_str) {
int child_str_length = child_str.length();
int[] prefix = new int[child_str_length];
// 得出所需要的前缀表
getPrefix(child_str,prefix,child_str_length);
// 将所得到的前缀表向后移动
movePrefix(prefix,child_str_length);
for(int one_index:prefix) {
System.out.println(one_index);
}
System.out.println("得到移动位置,下面进行字符串的匹配");
int child_str_index = 0;
int main_str_index = 0;
while(main_str_index < main_str.length()) {
if(child_str_index == child_str_length - 1 &&
child_str.charAt(child_str_index) == main_str.charAt(main_str_index)) {
System.out.println("找到一个了,位置就是:"+(main_str_index-child_str_length+1));
child_str_index = prefix[child_str_index];
}
if(main_str.charAt(main_str_index) == child_str.charAt(child_str_index)) {
child_str_index++;
main_str_index++;
}else {
child_str_index = prefix[child_str_index];
if(child_str_index == -1) {
child_str_index++;
main_str_index++;
}
}
}
}
整体的代码我会放在我的github上。
总结
KMP算法是查找章节中非常重要的一个算法,其基本思想不难,难在实现细节存在着很多代码优化,而这些细节也是算法非常重要的一部分。