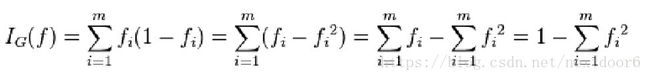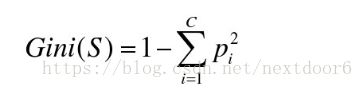决策树算法
决策树算法
决策树本质上是通过一系列规则对数据进行分类的过程。如何构造精度高、规模小的决策树是决策树算法的核心内容。
决策树学习通常包括3个步骤:
特征选择、决策树的生成和决策树的修剪。
特征选择:通过一种衡量标准,来计算通过不同特征进行分支选择后的分类情况,找出来最好的那个当成根节点,以此l类推,
而衡量的标准就是熵。
计算公式
熵值不确定性越大,得到的熵值也就越大。当p=0或p=1时,H(p)=0,随机变量完全没有不确定性。
当p=0.5时,H(p)=1,此时随机变量的不确定性最大,熵值最大。
一般通过信息增益的大小确定节点的位置,信息增益表示特征X使得类Y的不确定性减少的程度。
决策树的算法
ID3算法
根据信息增益确认的算法,选择信息增益最大的作为根节点,以此类推,如果像存在id为特征值的情况,分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大,但是这个特征作为根节点显然大大增加了决策树的分支。、
设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为:
![]()
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。也叫做系统熵。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
![]()
而信息增益即为两者的差值:
![]()
C4.5:信息增益率
C4.5算法流程与ID3相类似,只不过将信息增益改为信息增益比,以解决偏向取值较多的属性的问题,另外它可以处理连续型属性。通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足。
C4.5算法首先定义了“分裂信息”,其定义可以表示成:
![]()
其中各符号意义与ID3算法相同,然后,增益率被定义为:
![]()
C4.5算法选择具有最大增益率的属性作为分裂属性。
CART:使用GINI系数来做衡量标准。
Classification And Regression Tree,即分类回归树算法,简称CART算法,它是决策树的一种实现.
在CART算法中,基尼不纯度表示一个随机选中的样本在子集中被分错的可能性,基尼不纯度为这个样本被选中的概率乘以它被分错的概率。
假设y的可能取值为{1,2,...,m},令fi是样本被赋予i的概率,则基尼指数可以通过如下计算
则GINI系数公式为:
其中,Pi是S中类别i的概率。
示例
https://wenku.baidu.com/view/c9f049eec77da26925c5b08d.html
无论是分类树还是回归树,CART都要选择使子节点的GINI值或者回归方差最小的属性作为分裂的方案。
决策树减枝策略
预剪枝
边建立决策树边进行剪枝的操作,比较实用。
预剪枝:
限制深度,叶子节点个数,叶子节点样本树,信息增益量等。
后剪枝
当建立完决策树后来进行剪枝操作。
通过一定的衡量标准,叶子节点越多,损失越大。