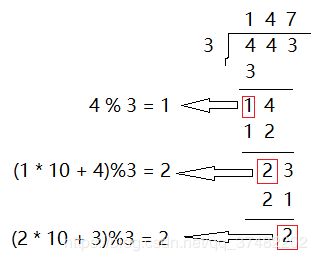JAVA 大数的乘法运算和取余运算
莫妒他长,妒长,则己终是短;莫护己短,护短,则己终不长。
1.乘法运算
这是一道入门的算法题,目的就是求两个超过基础数据类型所表示的两个数的乘积。
刚开始看到这道题我想的便是分解 计算 合并 ,但是合并后的数如何存储返回又是一个问题,苦思冥想下想到了用数组,并不断把算法优化。
首先实现这种大数运算,基础数据类型是无法存储也无法运算的,但是我们可以手写在纸上算
/**
* 7 8 9 6 5 2
* × 3 2 1 1
* -----------------
* 7 8 9 6 5 2 <---- 第1趟
* 7 8 9 6 5 2 <---- 第2趟
* .......... <---- 第n趟
* -----------------
* ? ? ? ? ? ? ? ? <---- 最后的值用另一个数组表示
*/要做的就是把这个过程实现为代码,首先我用的是把每次乘的结果用List存储,并做进位处理,然后每算完一行就加到最后的结果位上,这里还要做偏移处理,最后把List反向转换成数组,按顺序输出便是结果了。
private static Integer[] Method1(int[]arr1 , int[] arr2){
ArrayList result = new ArrayList<>(); //中间求和的结果
//arr2 逐位与arr1相乘
for(int i = arr2.length - 1; i >= 0; i--){
int carry = 0;
ArrayList singleList = new ArrayList<>();
//arr2 逐位单次乘法的结果
for(int j = arr1.length - 1; j >= 0; j--){
int r = arr2[i] * arr1[j] + carry;
carry = r / 10;
singleList.add(r % 10);
}
if(carry != 0){
singleList.add(carry);
}
int resultCarry = 0, count = 0;
int k = 0;
int l = 0;
int offset = arr2.length - 1 - i; //加法的偏移位
ArrayList middleResult = new ArrayList<>();
//arr2每位乘法的结果与上一轮的求和结果相加,从右向左做加法并进位
while (k < singleList.size() || l < result.size()) {
int kv = 0, lv = 0;
if (k < singleList.size() && count >= offset) {
kv = singleList.get(k++);
}
if (l < result.size()) {
lv = result.get(l++);
}
int sum = resultCarry + kv + lv;
middleResult.add(sum % 10); //相加结果从右向左(高位到低位)暂时存储,最后需要逆向输出
resultCarry = sum / 10;
count++;
}
if(resultCarry != 0){
middleResult.add(resultCarry);
}
result.clear();
result = middleResult;
}
Collections.reverse(result); //逆向输出结果
return result.toArray(new Integer[result.size()]);
} 但这样的效率真的低,因为List操作没有数组快,我就给改成了数组。
我先声明一个长为两个数组长度之和,宽为第二个数组长的数组,用于存储运算的每一行。
然后把每一列的值都加在对应的最后一行的位置上,并进行进位处理,返回最后一行的数组。
private static int[] Method2(int num1[],int num2[]){
int maxLength=num1.length+num2.length;
int[][] nums=new int[num2.length][maxLength];
for (int i=0;i=0;i--){
nums[num2.length-1][i]+=overflow;
for (int j=0;j 但是还可以优化的一点便是不再存储二维数组了,直接在最后的结果数组上操作,随后按数组从后到前统一处理进位。
private static int[] Method3(int num1[], int num2[]){
// 分配一个空间,用来存储运算的结果,num1长的数 * num2长的数,结果不会超过num1+num2长
int[] result = new int[num1.length + num2.length];
// 先不考虑进位问题,根据竖式的乘法运算,num1的第i位与num2的第j位相乘,结果应该存放在结果的第i+j位上
for (int i = 0; i < num1.length; i++){
for (int j = 0; j < num2.length; j++){
result[i + j + 1] += num1[i] * num2[j]; // (因为进位的问题,最终放置到第i+j+1位)
}
}
//单独处理进位
for(int k = result.length-1; k > 0; k--){
if(result[k] > 10){
result[k - 1] += result[k] / 10;
result[k] %= 10;
}
}
return result;
}在解决问题期间我还碰到了一种做乘法的算法,叫做Karatsuba算法,这种算法非常神奇,先看一张图
该图运算的是5678*1234,它首先把四位数拆分为两个两位数a,b,c,d,然后运算ac,bd,(a+b)(c+d),用第三个式子的结果减去前两个的结果,最后把该结果加上两个0,第一个式子的结果加上四个零,第二个式子的结果保持不动,将三个结果相加便是最后的结果。证明在这里。
这也就用到了递归,把大数分解为小数,知道可以运算,不过它运算的结果仍然不能超过long类型的表示范围,不过可以在其中加以改动最后使用数组表示,可以省去很多运算次数。
public static long karatsuba(long num1, long num2){
//递归终止条件
if(num1 < 10 || num2 < 10) return num1 * num2;
// 计算拆分长度
int size1 = String.valueOf(num1).length();
int size2 = String.valueOf(num2).length();
int halfN = Math.max(size1, size2) / 2;
/* 拆分为a, b, c, d */
long a = Long.valueOf(String.valueOf(num1).substring(0, size1 - halfN));
long b = Long.valueOf(String.valueOf(num1).substring(size1 - halfN));
long c = Long.valueOf(String.valueOf(num2).substring(0, size2 - halfN));
long d = Long.valueOf(String.valueOf(num2).substring(size2 - halfN));
// 计算z2, z0, z1, 此处的乘法使用递归
long z2 = karatsuba(a, c);
long z0 = karatsuba(b, d);
long z1 = karatsuba((a + b), (c + d)) - z0 - z2;
return (long)(z2 * Math.pow(10, (2*halfN)) + z1 * Math.pow(10, halfN) + z0);
}2.取余运算
我们只需要不断对每一位数字进行取余,把余数乘10加上后一位数继续取余,最后剩余的就是整个数的余数。
private static int bigNumMod(int bigNum[], int number){
int ans = 0;
for(int i = 0; i < bigNum.length; i++)
ans = ((ans * 10) + bigNum[i]) % number;
return ans;
}