自编码器概论
判定模型与生成模型
判定模型
对条件概率分布P(y|x)进行建模,即在特征x出现的情况下标记y出现的概率。其本质是根据X判定Y。
举例:若要确定一只羊是山羊还是绵羊,需从历史数据中训练得到判定模型,通过提取这只羊的特征来判断这只羊是山羊的概率大还是绵羊的概率。
生成模型
对联合概率分布P(x,y)进行建模,即特征x和标记y共同出现的概率。通过贝叶斯公式求得使p(yi|x)值最大的yi。其本质是联合概率分布可以理解为“生成”(X,Y)样本的依据。已知X,从Y的候选集中任选一个,可能有(X,Y1),…,(X,Yn),鉴于实际数据的“生成”方式依赖P(x,y),故我们选择概率最大者最为结果。
举例:若要确定一只羊是山羊还是绵羊,需根据山羊的特征训练出山羊模型,并根据绵羊的特征训练出绵羊模型,然后从这只羊中提取特征后依次与两个模型进行比对,结果为概率大者。
自编码器中的Decoder属于生成模型。
高效的数据表示
以下两组数据,哪组更容易记忆?
40,27,25,36,81,57,10,73,19,68
50,25,76,38,19,58,29,88,44,22,11,34,17,52,26,13,40,20[1]
尽管第一序列比第二序列短,但第二序列有明显规律。如果能够发现其规律,则除记住规律只需记住其第一个数字及序列长度即可,故第二序列更容易记忆。但假设某人记忆力超群,他可能不会关心数字序列是否存在规律。因此我们必须对自编码器增加约束以强制其探索数据中的规律。
注:
[1]此组数据为希尔顿序列,其规则是:偶数后一数字的值是其二分之一,奇数后一数字的值是其三倍加一。
什么是自编码器
自编码器(AutoEncoder,AE)是旨在使输出特征近似等于输入标记的自监督学习[1]神经网络。它借助稀疏编码的思想,捕捉并使用原始输入特征自身的稀疏高阶特征对其自身进行编码[2],再通过解码对原始输入特征进行复现。它通过数据有损压缩,从而挖掘数据集内部的精髓特征并达到降维的目的。
自编码器由Encoder[3]和Decoder[4]两部分组成。
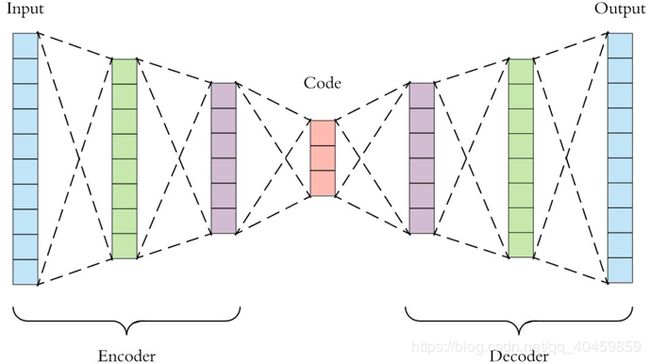
自编码器的结构如图1所示。其中Original Input指初始输入特征;Latent Representation指输入特征压缩表示后的稀疏高阶特征,即编码(code);Reconstructed Output指重构还原输入特征。
自编码器是一种数据压缩算法,其有以下三个特征:
- 数据相关性。自编码器只能压缩与训练数据类似的数据。
- 数据有损性。自编码器重构还原得到的输出标记与输入特征相比有一定程度的信息损失,且不可复原。我们通过损失函数衡量由于数据压缩而损失掉的信息。
- 自动学习性。自编码器模型能够从数据集中自动学习得到。
由于自编码器是在给定的一组数据集上进行训练,故在处理与训练集相似的数据时有绝佳的压缩效果。但若对解码器输入训练集中从未出现的编码,则输出标记可能是乱码或噪声。
注:
[1]自监督学习:自编码器不是一个真正的无监督学习算法,而是自监督学习算法。即其标签产生自输入数据。
[2]编码:输入特征的降维重构。它旨在将输入数据高效表示。
[3]Encoder:编码器,又称识别网络。它旨在将输入特征压缩为高阶特征并学习之。
[4]Decoder:解码器,又称生成网络。它旨在将高阶特征重构还原成原始输入数据。
编码器
编码器的核心任务是提取原始输入特征的“精髓”,即降维。因此编码器中各层神经元数量呈现逐层减少的趋势。此举起到压缩维度,提取原始输入特征中重要信息的作用。
实际应用中,有时训练完成自编码器后只使用其中的编码器部分。将编码器部分输出的降维浓缩数据喂入神经网络进行监督学习,“去粗取精”有助于提高监督学习的正确率。
解码器
解码器的核心任务是将编码器输出的原始输入特征的稀疏高阶特征进行重构还原,并输出与原始输入特征维度相同的输出标记。并将输出标记与原始输入特征的误差,即数据压缩的信息损失,进行反向传播。但并非输出标记与原始输入特征相似度越高越好,相似度过高易产生过拟合,但我们希望其有很强的泛化能力。
通俗的讲,我们可以将解码器的工作看作将原始输入特征的稀疏高阶特征解压成原始输入特征,其提供的功能与解压器和生成器十分类似。
工作流程
- 正向传播过程:自编码器的正向传播过程与传统神经网络完全相同,即将原始输入特征送至输入层,经隐藏层后送至输出层输出。自编码器的特点是输入层与输出层的维度完全相同。
- 反向传播过程:将输出标记与原始输入特征进行比较,以两者的差异作为误差进行反向传播。
约束条件
降维限制
降维限制即限制隐藏层神经元数量。由于隐藏层神经元数量小于输出层神经元数量与输出层神经元数量,故编码器只能学习原始输入特征中的精髓,而去除非精髓特征。
加入噪声
由于原始输入特征中加入了噪声,故而达到了防止原始输入特征与输出标记完全相同的目的。
自编码器的应用
- 数据去噪。
- 数据降维。
- 特征抽取。自编码器(AutoEncoder)将原始输入特征输入至编码器(Encoder)得到中间向量,即编码(code)。将编码(code)输入至解码器(Decoder)得到输出标记。若输出标记近似等于原始输入特征,则中间向量可作为输入向量的特征向量。我们通过调整编码器(Encoder)和解码器(Decoder)的参数,使原始输入特征与输出标记误差最小[1],从而寻找特征向量。
注:
[1]输出标记是无标签数据,故根据自编码器的特点,误差是输出标记与原始输入特征比对后的结果。
自编码器的分类
- 欠完备自编码器
- 正则自编码器
- 去噪自编码器
- 收缩自编码器
- 栈式自编码器
- 变分自编码器