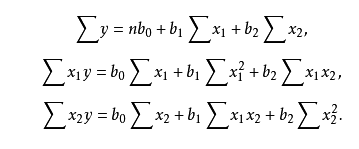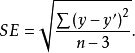多元线性回归
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
公式
——多元线性回归模型
1.建立模型
以二元线性回归模型为例 ,二元线性回归模型如下:
类似的使用最小二乘法进行参数估计:
2.拟合优度指标
标准误差:对y值与模型估计值之间的离差的一种度量。其计算公式为:
3.置信范围
置信区间的公式为:置信区间=
估计方法
1.普通最小二乘法
普通最小二乘法(Ordinary Least Square, OLS)通过最小化误差的平方和寻找最佳函数。通过矩阵运算求解系数矩阵:
2.广义最小二乘法
广义最小二乘法(Generalized Least Square)是普通最小二乘法的拓展,它允许在误差项存在异方差或自相关,或二者皆有时获得有效的系数估计值。公式如:
分析
1、多元回归分析与简单线性回归区别
多个自变量x
2、多元回归模型
3、多元回归方程
4、估计多元回归方程
一个样本被用来计算
的点估计
5、估计流程(与简单线性回归类似)
6、估计方法
使sum of squares最小,
运算与简单线性回归类似,涉及线性代数和矩阵代数的运算
7、举例
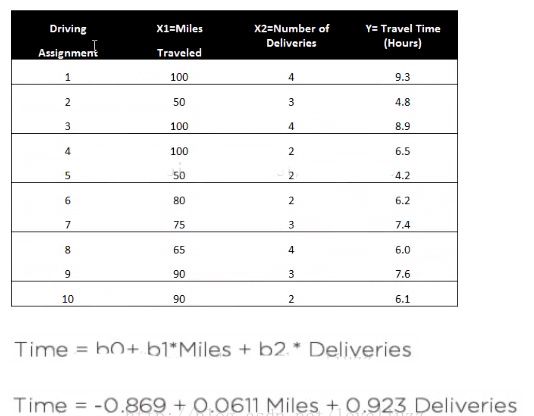
一家快递公司送货,X1:运输里程;X2:运输次数;Y:总运输时间
8、描述参数含义
b1:平均每多送1英里,运输时间延长0.0611小时
b2:平均每多一次运输,运输时间延长0.923小时
9、预测
问题:如果一个运输任务是跑102英里,运输6次,预计时间是多长?
10、如果自变量里面有分类型变量(categorical data),如何处理?
11、对第一个表格的数据,快递公司运输问题用Python进行代码实现
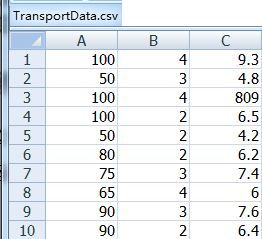
将运输里程、运输次数、总运输时间按列的形式保存到文件TransportData.csv文件中,如下图:
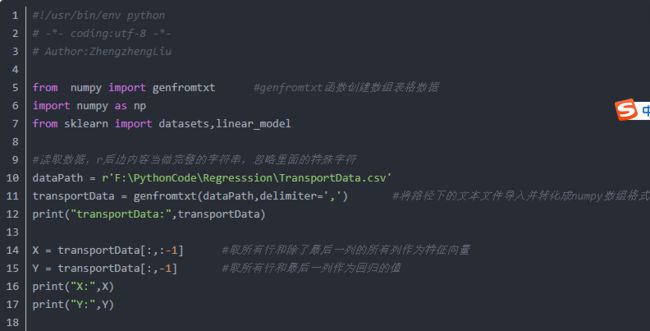
Python3.7实现代码为:
运行结果:
transportData: [[ 100. 4. 9.3]
[ 50. 3. 4.8]
[ 100. 4. 8.9]
[ 100. 2. 6.5]
[ 50. 2. 4.2]
[ 80. 2. 6.2]
[ 75. 3. 7.4]
[ 65. 4. 6. ]
[ 90. 3. 7.6]
[ 90. 2. 6.4]]
X: [[ 100. 4.]
[ 50. 3.]
[ 100. 4.]
[ 100. 2.]
[ 50. 2.]
[ 80. 2.]
[ 75. 3.]
[ 65. 4.]
[ 90. 3.]
[ 90. 2.]]
Y: [ 9.3 4.8 8.9 6.5 4.2 6.2 7.4 6. 7.6 6.4]
coefficients: [ 0.06231881 0.88000431]
intercept: -0.807517256255
y_pred: [ 10.82902718]
12、当自变量中有分类变量(如:车型)时,多元线性回归处理
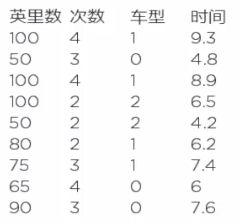
将分类变量转化成0,1,2等数字来表示。0:小车,1:SUV,2:卡车,转码格式为:用一个3维数表示,所用车辆类型为1,其余车型为0.
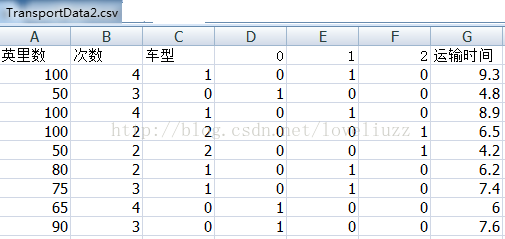
将运输里程、运输次数、运输车型、总运输时间按列的形式保存到文件TransportData2.csv文件中,转码格式如下图:
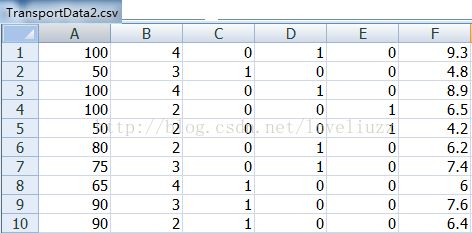
将转码后的数据保存在TransportData2.csv文件中:
总结
好啦,以上是线性回归算法,我希望自己能多专研机器学习方面的知识并结合实例进行阐述。
让人遗憾的是,不支持数学公式,所以我大部分地方是从我的word文档里面贴图过来的,花费我大量的时间不说,可能有些地方难免会失去数学本来的味道。
写这篇文章的目的,一是帮助自己加深对机器学习算法的理解;二是很希望能帮助到需要的同学,大家共同进步。
本人知识水平有限,如有错误之处,还请大家多多谅解。