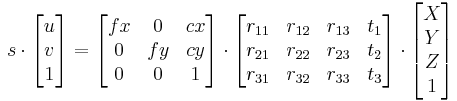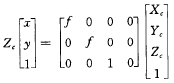相机模型——针孔相机

        想到学习下相机模型，是因为最近做的事情涉及到求解相机参数、恢复相机位置等。而在这里开博，主要也是当做学习笔记来用。其中【】表示引用和参考。

        在相机模型中，针孔相机是相对简单而常用的模型。简单的说，针孔相机模型就是把相机简化成小孔成像，如图1【3】，f标注的距离是焦距。可以想见，这种简化对于精度要求高的情况或者广角相机是不适用的。但由于其用的是投影成像的方法，因此要先了解下投影变换。

图1

        比较基础简单的投影变换有正交变换和透视变换。正交变换就是物体上的点全都平行地投射到投影面，没有远近的区别，即没有透视效果。透视变换正好相反，被投影物体处于一个四棱台区域中，物体被投影到离相机较近的平面上。相机被抽象为一个点，而投影点是物体上的点和相机的连线与投影平面的交点。由于投影的路径不再相互平行，因此会产生透视效果，这个随便自己画下就明白了。具体可以参考【1】。

        针孔相机模型是基于透视变换的相机模型。其公式如图2【2】，而以字母表示矩阵，则如图3【2】。

图2

图3

其中m‘为屏幕uv坐标，A为相机内参，[R|t]为相机外参，M’为物体世界坐标，而s为物体在相机坐标系中的z坐标，这是公式推导过程中产生的参数。这里提到的相机内参是指仅由相机本身决定的参数，也就是对某一相机一旦这个值算好就不用再次进行计算。相对的，外参是和世界坐标系和相机位置有关的。

       那么这个公式是如何产生的呢？相机模型是属于计算机3d视觉中的，而所谓3d视觉就是要建立二维图像和三维场景的联系，比较主要的一个用途是根据二维图片重建三维场景。所以一个自然的想法就是通过各种方式使得可以从三维坐标计算得到屏幕空间坐标或者相反。在进行推导之前，先要普及下齐次坐标的知识，因为所有推导都是在齐次坐标系下进行的。齐次坐标简单的来说就是将原来的坐标添加一个维度，比如[x,y,z]在齐次坐标系下就是[nx,ny,nz,n](n!=0)，其中n为多少是无所谓的。针对于相机模型这个话题，也只会将[x,y,z]变为[x,y,z,1]。在对于图形图像的处理中，大量的使用到齐次坐标，因为这样在非齐次坐标系下需要通过加法进行的运算就都可以合并到乘法运算中去了，也就是合并为一个参数矩阵，各种方便。

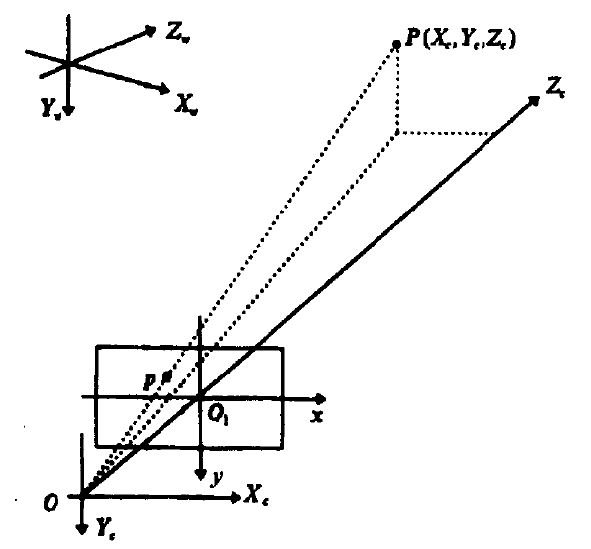
        想要推导这个公式，就要先分析相机及其所处环境的模型。将世界中的物体映射到屏幕上的整个过程，涉及四个坐标系。首先是世界坐标系，这个不用多说了。而相机本身也是世界中的物体，因此在世界坐标系中也有一个位置。但是还需要一个相对与相机位置不变的相机坐标系。一般这个坐标系的原点设在抽象出的针孔相机处，z轴为光轴。而相机的投影平面存在两个坐标系。投影平面是和相机相隔焦距距离并垂直于光轴的平面，一般位于z的正方向。这两个坐标系最大的区别是一个像前两个坐标系一样使用浮点数，其原点位于光轴和和投影平面的交点处，x、y轴与相机坐标系对应轴平行，如图4【4】。将三维空间物体投影到这样一个平面坐标系上是很直观的，但是对于计算机的显示来说，不但要求位置以像素为单位表示，而且最好值全是正数，才符合编程的需要。因此就产生了第四个坐标系——uv坐标系。这个坐标系的原点在显示屏幕的一个角上，使得显示部分全落在第一象限，同时坐标值是以像素为单位的正数。uv坐标和平面浮点坐标关系如图5【4】。

图4

图5

        在此要注意下相机坐标系部分模型和实际相机的关系。实际相机的朝向在相机坐标系中应当是朝向负z方向，也是景物真实所在的方向。而在图4和很多其他图中都将真实景物的位置绘制在正z方向，个人理解是这样在推导上比较直观。景物在真实的位置，还要将投影好的影像颠倒位置才合理，而将其假想在负方向，不但推导容易，而且直接就得出所需的结果。

        接下来就是详述如何进行公式的推导了。这部分基本参考马颂德等人的《计算机视觉》一书中的推导。

        首先是由世界坐标系转换到相机坐标系，这部分使用图形学中基础的旋转平移矩阵的推导，不详述了，以后有时间再补上。可以得到如下等式，如图6

图6

其中，带有下标w的代表世界坐标系，而带有下标c的表示相机坐标系，R、t分别表示旋转与平移矩阵。

        继而是由相机坐标系到投影平面的转换，使用的是相似三角形的原理，有如图7所示关系。由于全部过程使用齐次坐标系，对于这个关系也尽量使用齐次坐标和矩阵，如图8。Zc这个系数被单独放在等号左边作为系数，是为了凑出[Xc, Yc, Zc, 1]。

图7

图8

        之后处理投影平面上的坐标系转换，其中使用浮点数作为单位的坐标系，在此称为浮点平面坐标系。uv坐标系和浮点平面坐标系的关系如图5所示。在这里注意到《计算机视觉》中的图示都是y轴向下的，感觉是因为uv坐标的原点是设置在屏幕左上角，v轴向下的。这样设置是由于习惯还是计算机显存将较高部分像素标记为较小序号等原因还没有考证过，但是可以想见y轴都向下是为了推导方便，而且如果全部翻转向上应该也是没有影响的。

设想uv坐标系中每个像素在浮点平面坐标系中在x方向长dx，在y方向长dy，浮点平面坐标系在uv坐标系中的位置是（u0, v0）。则它们有如图9所示关系。依旧要用齐次坐标表示，如图10。

图9

图10

        至此，便可以将几个矩阵合并，最终得到一个uv坐标系与世界坐标系的关系，如图11。可以注意到内参全部是由相机本身确定的，而外参是需要根据相机位置变化的。

图11

参考资料

【1】http://netclass.csu.edu.cn/NCourse/hep089/Chapter5/CG_Txt_5_033.htm

【2】http://wiki.opencv.org.cn/index.php/Cv%E7%85%A7%E7%9B%B8%E6%9C%BA%E5%AE%9A%E6%A0%87%E5%92%8C%E4%B8%89%E7%BB%B4%E9%87%8D%E5%BB%BA

【3】http://baike.baidu.com/view/104209.htm?fr=aladdin

【4】《计算机视觉》，马松德等