语音增强之OMLSA
OMLSA
OM-LSA算法,全称为optimally-modified log-spectral amplitude,中文有翻译为“最优改进对数谱幅度估计”,OMLSA算法相比较其它抑制算法有较少的音乐噪声残留(due to its superiorityin reducing musica noise phenomena)
先看系统框图
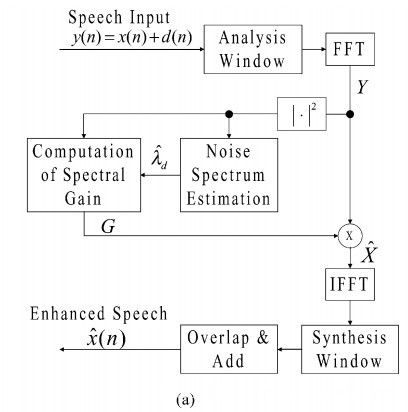 流程跟其它降噪方法什么不同,信号输入->STFT->噪声估计/增益计算->频谱修改->iSTFT
流程跟其它降噪方法什么不同,信号输入->STFT->噪声估计/增益计算->频谱修改->iSTFT
这里核心部分就是噪声估计然后计算频域增益了,这一步的框图如下
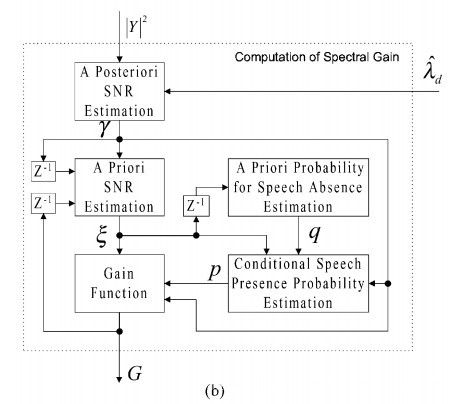
这里就主要分析增益函数的计算过程
- signal model
y ( n ) = x ( n ) + d ( n ) y(n) = x(n)+d(n) y(n)=x(n)+d(n)
-
STFT
Y ( k , l ) = X ( k , l ) + D ( k , l ) Y(k,l)=X(k,l)+D(k,l) Y(k,l)=X(k,l)+D(k,l)estimate is obtained by applying a specific gain function to each spectral component of the noisy speech signal
X ^ ( k , l ) = G ( k , l ) Y ( k , l ) \hat{X}(k,l)=G(k,l)Y(k,l) X^(k,l)=G(k,l)Y(k,l)
LSA估计器以最小化下式为优化目标
E { ( l o g A ( k , l ) − l o g A ^ ( k , l ) ) 2 } E\begin{Bmatrix}(logA(k,l)-log\hat{A}(k,l))^2\end{Bmatrix}{} E{(logA(k,l)−logA^(k,l))2}
其中, A ^ ( k , l ) ) \hat{A}(k,l)) A^(k,l))为估计得到的幅度谱
直接给出OM-LSA的表达式如下
G ( k , l ) = G H 1 ( k , l ) p ( k , l ) G m i n 1 − p ( k , l ) G(k,l)=G_{H_1}(k,l)^{p(k,l)}G_{min}^{1-p(k,l)} G(k,l)=GH1(k,l)p(k,l)Gmin1−p(k,l)
其中:
G H 1 G_{\mathrm{H}_{1}} GH1表示语音存在时候的条件增益
G m i n G_{min} Gmin为增益下限,也可以理解为当语音不存在时候的条件增益
p ( k , l ) p(k,l) p(k,l)为语音存在概率
继续给出增益函数中的未知量
G H 1 ( k , ℓ ) = ξ ( k , ℓ ) 1 + ξ ( k , ℓ ) exp ( 1 2 ∫ ν ( k , ℓ ) ∞ e − t t d t ) G_{\mathrm{H}_{1}}(k, \ell)=\frac{\xi(k, \ell)}{1+\xi(k, \ell)} \exp \left(\frac{1}{2} \int_{\nu(k, \ell)}^{\infty} \frac{\mathrm{e}^{-t}}{t} \mathrm{d} t\right) GH1(k,ℓ)=1+ξ(k,ℓ)ξ(k,ℓ)exp(21∫ν(k,ℓ)∞te−tdt)
ξ ( k , ℓ ) ≜ λ x ( k , ℓ ) λ d ( k , ℓ ) \xi(k, \ell) \triangleq \frac{\lambda_{x}(k, \ell)}{\lambda_{d}(k, \ell)} ξ(k,ℓ)≜λd(k,ℓ)λx(k,ℓ)
v ( k , ℓ ) ≜ γ ( k , ℓ ) ξ ( k , ℓ ) 1 + ξ ( k , ℓ ) v(k, \ell) \triangleq \frac{\gamma(k, \ell) \xi(k, \ell)}{1+\xi(k, \ell)} v(k,ℓ)≜1+ξ(k,ℓ)γ(k,ℓ)ξ(k,ℓ)
γ ( k , ℓ ) ≜ ∣ Y ( k , ℓ ) ∣ 2 λ d ( k , ℓ ) \gamma(k, \ell) \triangleq \frac{|Y(k, \ell)|^{2}}{\lambda_{d}(k, \ell)} γ(k,ℓ)≜λd(k,ℓ)∣Y(k,ℓ)∣2
其中,
ξ ( k , ℓ ) \xi(k, \ell) ξ(k,ℓ)为先验信噪比(priori SNR)
γ ( k , ℓ ) \gamma(k, \ell) γ(k,ℓ)为后验信噪比(posteriori SNR)