无人车系统(六):轨迹跟踪Stanley方法
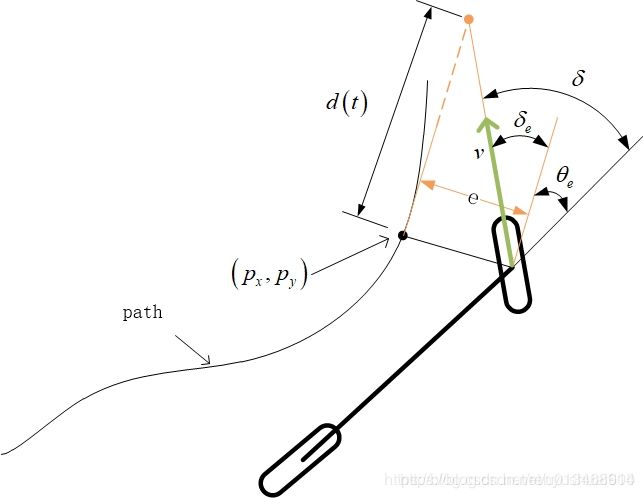
前面介绍的Pure Pursuit方法利用无人车的横向跟踪误差来设计控制器。在无人车轨迹跟踪任务中,除了横向跟踪误差外,是否还有其他信息有助于提高控制器的稳定性与有效性。本篇介绍的Stanely方法就结合横向跟踪误差 e y e_y ey与航向角偏差 e θ e_{\theta} eθ来设计控制器。值得注意的是,Stanley计算横向跟踪误差与pure pursuit方法是有区别的,Pure pursuit是以后轴中心为基准点计算几何学公式,而Stanley是基于前轴中心为基准点计算几何学公式的。
Stanley 方法分析与控制器设计
参照无人驾驶算法——使用Stanley method实现无人车轨迹追踪
Stanley 控制器设计如下:
δ ( k ) = θ e ( k ) + arctan λ e ( k ) v ( k ) \delta(k)=\theta_{e}(k)+\arctan \frac{\lambda e(k)}{v(k)} δ(k)=θe(k)+arctanv(k)λe(k)
其中, θ e ( k ) \theta_e(k) θe(k)为 k k k时刻的航向角偏差, e ( k ) e(k) e(k)为根据上图几何学计算的横向跟踪误差, λ \lambda λ为需要调节的参数, v v v为无人车当前速度。
2. python示例
参数 λ = 2.0 \lambda=2.0 λ=2.0,速度为常值 v = 2.0 v=2.0 v=2.0
"""
Stanley method
"""
import numpy as np
import math
import copy
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
plt.figure(figsize=(18, 3))
class UGV_model:
def __init__(self, x0, y0, theta0, L, v0, T): # L:wheel base
self.x = x0 # X
self.y = y0 # Y
self.theta = theta0 # headding
self.l = L # wheel base
self.v = v0 # speed
self.dt = T # decision time periodic
def update(self, vt, deltat): # update ugv's state
dx = self.v*np.cos(self.theta)
dy = self.v*np.sin(self.theta)
dtheta = self.v*np.tan(deltat)/self.l
self.x += dx*self.dt
self.y += dy*self.dt
self.theta += dtheta*self.dt
def plot_duration(self):
plt.scatter(self.x, self.y, color='r')
plt.axis([self.x-9, self.x+9, -3, 3])
# plt.axis([self.x-9, self.x+9, -10, 10])
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
from scipy.spatial import KDTree
# set reference trajectory
refer_path = np.zeros((1000, 2))
refer_path[:,0] = np.linspace(0, 1000, 1000)
refer_head = np.zeros(1000)
# refer_path[:,1] = 5*np.sin(refer_path[:,0]/5.0)
refer_tree = KDTree(refer_path)
plt.plot(refer_path[:,0], refer_path[:,1], '-.b', linewidth=5.0)
ugv = UGV_model(0, 1.0, 0, 2.0, 2.0, 0.1)
k = 2.0
pind = 0
ind = 0
for i in range(1000):
robot_state = np.zeros(2)
robot_state[0] = ugv.x
robot_state[1] = ugv.y
_, ind = refer_tree.query(robot_state)
if ind < pind:
ind = pind
else:
pind = ind
dist = np.linalg.norm(robot_state-refer_path[ind])
dx, dy = refer_path[ind] - robot_state
alpha = math.atan2(dy, dx)
e = np.sign(np.sin(alpha-ugv.theta))*dist
dtheta = refer_head[ind]-ugv.theta
delta = dtheta+math.atan2(k*e/ugv.v, 1.0)
ugv.update(2.0, delta)
ugv.plot_duration()
以上