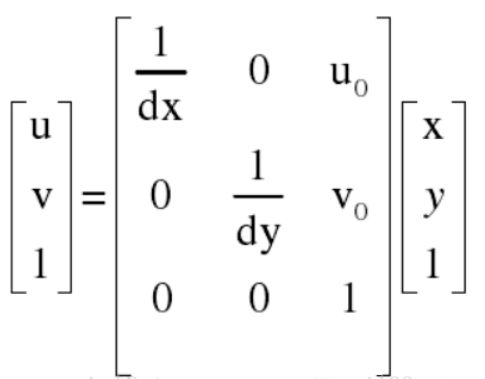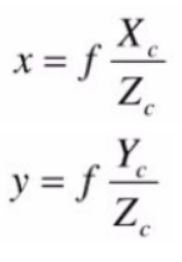图像坐标系、相机坐标系和世界坐标系 相机的内、外参数矩阵

图像坐标系、相机坐标系和世界坐标系的定义，及三者之间的变换关系。

图像坐标系

1.图像像素坐标系

原点：图像左上角P0点
单位：像素
横坐标u：图像数组中的列数
纵坐标v：图像数组中的行数

2.图像物理坐标系
在图像像素坐标系下建立以物理单位（以下均假设为mm）表示的坐标系，使像素尺度具有物理意义。
原点：主点（相机光轴与图像平面的交点，一般位于图像平面中心，即图中O1点）
单位：mm/像素
横轴x轴：与像素坐标系下的u轴平行
纵轴y轴：与像素坐标系下的v轴平行

3.图像像素坐标系与图像物理坐标系的转换关系：

其中：
dx为每个像素在横轴x上的尺寸，dy为每个像素在纵轴y上的尺寸。

将其写成矩阵形式：

相机坐标系

图中：xy平面为图像平面

原点：摄像机光心O点
Xc轴：与图像坐标系x轴平行
Yc轴：与图像坐标系y轴平行
Zc轴：摄像机光轴，与图像平面垂直
OO1=f（焦距）

图像物理坐标系和相机坐标系的转换关系：

世界坐标系

世界坐标系用来描述相机的位置，即相机坐标系原理图中的Ow-XwYwZw坐标系。

相机坐标系与世界坐标系的转换关系：

其中:
R为旋转矩阵，是x，y，z三个轴向旋转矩阵的乘积，即R=RxRyRz。
T为平移向量，表示三个轴向上的平移距离，即T=[Tx,Ty,Tz]T（上标表转置）。
Lw为由旋转平移构成的一个4*4的矩阵。

由上述对三个坐标系之间的转换可以推导得到图像像素坐标系和世界坐标系的转换关系：

相机的内、外参数矩阵，实际中你能结合身边的实例(如电脑摄像头、手机镜头)说明这些参数的大致值么？

相机内参数是与相机自身特性相关的参数，比如相机的焦距、像素大小等；

相机外参数是在世界坐标系中的参数，比如相机的位置、旋转方向等。

佳能 70D相机：

参数：

采用焦距f​：50 mm
分辨率采用：1920x1080
传感器尺寸：22.5x15 mm
计算内参数：

u0=19202=960​、v0=10802=540​、dx=22.51920=0.0117​、dy=151080=0.0139​
ax=fdx=4266.67、ay=fdy=360

使用线性法求解相对位姿时的要求输入和输出，以及求解的基本思想。

基于空间多点相对位姿测量

通过相机标定或者相机自身参数计算获取相机内参数和畸变系数
建立世界坐标系转换为像素坐标系的方程
目的是求解外参数矩阵的旋转向量和平移向量
通过方程组的变换，消去第三维的坐标，最后得到一个关于旋转向量和平移向量的公式。
扩展到多个点的情况下，有六个或以上的特征点且非共面的时候，就可解得一个关于旋转向量和平移向量的矩阵组
利用矩阵的QR分解，得到最终的旋转矩阵和平移矩阵。
最后通过旋转矩阵计算旋转角，使得相机坐标系和世界坐标系完全平行。
注意：在实现过程中，一般使用solvePnP方法进行计算，传入参数：目标坐标系的3D点，图像平面点坐标，相机内参数，畸变系数，最后就可以得到旋转向量和平移向量

输入信息

相机的内参数
多个空间上的特征点(非共面)在目标坐标系(3D)和相平面坐标系(2D)坐标。
输出信息

目标坐标系相对相机坐标系的位置和姿态。

基于平面多特征点相对位姿测量

通过相机标定或者相机自身参数计算获取相机内参数和畸变系数
建立世界坐标系转换为像素坐标系的方程
目的是求解外参数矩阵的旋转向量和平移向量
通过方程组的变换，消去第三维的坐标，最后得到一个关于旋转向量和平移向量的公式。
扩展到多个点的情况下，有四个或以上的特征点且非共面的时候，就可解得一个关于旋转向量和平移向量的矩阵组
利用矩阵的QR分解，得到最终的旋转矩阵和平移矩阵。
最后通过旋转矩阵计算旋转角，使得相机坐标系和世界坐标系完全平行。
注意：在实现过程中，一般使用solvePnP方法进行计算，传入参数：目标坐标系的3D点，图像平面点坐标，相机内参数，畸变系数，最后就可以得到旋转向量和平移向量

输入信息

相机内参数
多个平面上的特征点在目标坐标系(3D)和相平面坐标系(2D)坐标
输出信息

目标坐标系相对相机坐标系的位置和姿态。

使用Zhang方法进行相机标定需要的输入条件和得到的具体输出量，以及Zhang方法的主要步骤

输入条件

目标物体的多个pose的图片数据，一般最少30张。

通过图片数据，获取目标坐标系的3D点和图像平面点坐标。

输出量

相机内参数矩阵

畸变系数

旋转变量

平移变量

主要步骤

设定标定板

旋转标定板或相机，采集标定板图像的不同pose

对一个pose,计算单应矩阵(类似M矩阵)

有三个以上Pose，根据各单应矩阵计算线性相机参数

使用非线性优化方法计算非线性参数

最后得到相机内参数、矩阵畸变系数以及每张图片的旋转变量和平移变量。