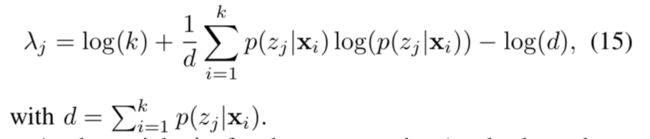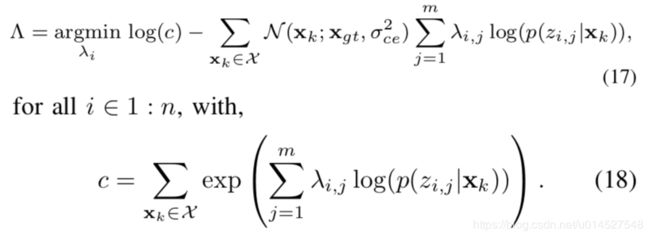基于WIFI指纹的室内定位
读了一篇关于wif定位的文章,感觉不错:
Miyagusuku R , Yamashita A , Asama H . Data Information Fusion From Multiple Access Points for WiFi-Based Self-localization[J]. IEEE Robotics and Automation Letters, 2019, 4(2):269-276.

基于WIFI的指纹室内定位流程见上:
1.首先基于预先采集的数据库建立pose-rssi的映射关系;
2.基于当前获取的WIFI信号和预先建立的pose-rssi映射关系获取当前测量的位置概率;
4.基于概率融合算法将每个AP的概率进行融合,得到联合概率分布;
文中主要关注于能够提升联合概率计算效率和性能的数据融合算法。
1. 数据融合模型
首先,基于预先采集的数据,建立地图中位置(x, y)- 均值和方差(u, σ \sigma σ)之间的映射关系模型。
地图中的每个位置点都被假设是正太分布,在一个任意位置x观测到信号z的概率为:
p ( z ∣ x ∗ ) = 1 s d [ z ∗ ] ψ ( E [ z ∗ ] − z s d [ z ∗ ] ) p(z|x_*)=\frac{1}{sd[z_*]}\psi(\frac{E[z_*]-z}{sd[z_*]}) p(z∣x∗)=sd[z∗]1ψ(sd[z∗]E[z∗]−z)
上式中 E [ z ∗ ] E[z_*] E[z∗]和 s t d [ z ∗ ] std[z_*] std[z∗]是在模型 x ∗ x_* x∗处预测的均值和标准差。此处也可以用其他的概率模型代替来计算P(z|x)。
我们感兴趣的是基于一个WIFI测量z下位置 x ∗ x_* x∗的后验概率 P ( x ∣ z ) P(x|z) P(x∣z),使用贝叶斯法则进行计算:
p ( x ∣ z ) [ = ] p ( z ∣ x ) ∗ p ( x ) p(x|z) [=] p(z|x)*p(x) p(x∣z)[=]p(z∣x)∗p(x)
基于m个AP和m个WIFI模型,问题转化为找到一个合适的联合概率函数 p ( z 1 , z 2 , . . . , z m ∣ x ) p(z_1, z_2, ..., z_m|x) p(z1,z2,...,zm∣x):
p ( z 1 , z 2 , . . . , z m ∣ x ) = p ( z 1 ∣ x ) p ( z 2 ∣ z 1 , x ) . . . p ( z m ∣ z 1 , z 2 . . . , z m − 1 , x ) . . . . . . ( 3 ) p(z_1, z_2, ..., z_m|x) = p(z_1|x)p(z_2|z_1, x)...p(z_m|z_1, z_2..., z_{m-1}, x) ...... (3) p(z1,z2,...,zm∣x)=p(z1∣x)p(z2∣z1,x)...p(zm∣z1,z2...,zm−1,x)......(3)
现有的两种进行WIFI概率融合的方法分布是基于信号强度 z i z_i zi不同的独立性假设推导出的。
1.1 概率模型点积
若假设两两测量 z p z_p zp和 z q z_q zq在给定的位置点x是条件独立的,则有:
p ( z p ∣ z q , x ) = p ( z p ∣ x ) , ∀ p ≠ q . . . . . . ( 4 ) p(z_p|z_q, x) = p(z_p|x), {\forall} p \neq q......(4) p(zp∣zq,x)=p(zp∣x),∀p=q......(4)
因此可以根据公式(3)和(4)得到概率模型的点积形式:
p ( z 1 , z 2 , . . . , z m ∣ x ) = ∏ i = 1 m p ( z i ∣ x ) p(z_1, z_2,..., z_m|x) = \prod_{i=1}^mp(z_i|x) p(z1,z2,...,zm∣x)=i=1∏mp(zi∣x)
假设在给定位置下所有的独立概率与其他概率之间都是条件独立,此为一个有效的假设。但是这样的后验分布通常会导致过拟合,这是使用几个模型进行序贯贝叶斯更新的普遍问题。
1.2 指数模型点积
按照条件概率的一般公式,我们可以得到:
p ( z p , z q ∣ x ) = p ( z p ∣ x ) p ( z q ∣ z p , x ) p(z_p, z_q|x) = p(z_p|x)p(z_q|z_p, x) p(zp,zq∣x)=p(zp∣x)p(zq∣zp,x)和 p ( z p , z q ∣ x ) = p ( z q ∣ x ) p ( z p ∣ z q , x ) p(z_p, z_q|x) = p(z_q|x)p(z_p|z_q, x) p(zp,zq∣x)=p(zq∣x)p(zp∣zq,x),将两者相乘可得:
p ( z p , z q ∣ x ) 2 = p ( z p ∣ x ) p ( z q ∣ z p , x ) p ( z q ∣ x ) p ( z p ∣ z q , x ) p(z_p, z_q|x)^2 = p(z_p|x)p(z_q|z_p, x)p(z_q|x)p(z_p|z_q, x) p(zp,zq∣x)2=p(zp∣x)p(zq∣zp,x)p(zq∣x)p(zp∣zq,x)
若所有模型之间都假设是完全独立的,则上式可以重写为:
p ( z p , z q ∣ x ) 2 = p ( z p ∣ x ) p ( z q ∣ x ) p ( z q ∣ x ) p ( z p ∣ x ) p(z_p, z_q|x)^2 = p(z_p|x)p(z_q|x)p(z_q|x)p(z_p|x) p(zp,zq∣x)2=p(zp∣x)p(zq∣x)p(zq∣x)p(zp∣x)
所以:
p ( z p , z q ∣ x ) = p ( z p ∣ x ) 1 / 2 p ( z q ∣ x ) 1 / 2 p(z_p, z_q|x) = p(z_p|x)^{1/2}p(z_q|x)^{1/2} p(zp,zq∣x)=p(zp∣x)1/2p(zq∣x)1/2
基于此假设和公式(3)可得,m个模型时的概率融合公式为:
p ( z 1 , z 2 , . . . , z m ∣ x ) = ∏ j = 1 m p ( z j ∣ x ) 1 / m p(z_1, z_2,..., z_m|x) = \prod_{j=1}^mp(z_j|x)^{1/m} p(z1,z2,...,zm∣x)=j=1∏mp(zj∣x)1/m
此便为指数模型的点积形式。该方法通过平滑的方式解决了上一个方法的过拟合问题,但是此方法容易生成欠拟合的结果。不过,在实际使用贝叶斯滤波时,这些欠拟合的预测方法一般要好于概率点积的过拟合方法
1.3 一般指数模型点积
上述的两个方法均将所有的单个概率的权重认为是相同的。但是实际中,对于每一个位置来说,每一个wifi提供的信息量是不一样的。此处同样使用完全独立假设。将 p ( z p ∣ x ) p ( z q ∣ z p , x ) p(z_p|x)p(z_q|z_p, x) p(zp∣x)p(zq∣zp,x)和 p ( z q ∣ x ) p ( z p ∣ z q , x ) p(z_q|x)p(z_p|z_q, x) p(zq∣x)p(zp∣zq,x)分别增加 λ p 和 λ q \lambda_p和\lambda_q λp和λq的指数操作,并相乘。
p ( z p , z q ∣ x ) λ p + λ q = p ( z p ∣ x ) λ p p ( z q ∣ x ) λ q p(z_p, z_q|x)^{\lambda_p + \lambda_q} = p(z_p|x)^{\lambda_p}p(z_q|x)^{\lambda_q} p(zp,zq∣x)λp+λq=p(zp∣x)λpp(zq∣x)λq
所以, 对于m个模型:
p ( z 1 , z 2 , . . . , z m ∣ x ) = ( ∏ j = 1 m p ( z j ∣ x ∗ ) λ j ) 1 / ∑ j = 1 m λ j p(z_1, z_2,..., z_m|x) = (\prod_{j=1}^mp(z_j|x_*)^{\lambda_j})^{1/\sum_{j=1}^m{\lambda_j}} p(z1,z2,...,zm∣x)=(j=1∏mp(zj∣x∗)λj)1/∑j=1mλj
此一般指数模型点类似于独立概率的几何加权平均。
下图3表示了在室内环境计算后验分布的结果,使用上述的方法,并在给定位置上假设先验为均匀分布。如图所示,使用一般指数模型可以得到更合适的后验分布。

2. 权重计算方法
2.1 最小熵(gPoE minH)
2.2 信息增益(gPoE deltaH)
2.3 高斯过程(gPoE GP)
3. 实验测试
对于所有的方法,wifi模型均使用文献[6]中所述方法进行学习。实验过程采用蒙特卡洛的方法进行模拟:
[6] R. Miyagusuku, A. Yamashita, and H. Asama, “Precise and accurate wireless signal strength mappings using Gaussian processes and path loss models,” Robotics and Autonomous Systems, vol. 103, pp. 134– 150, 2018.
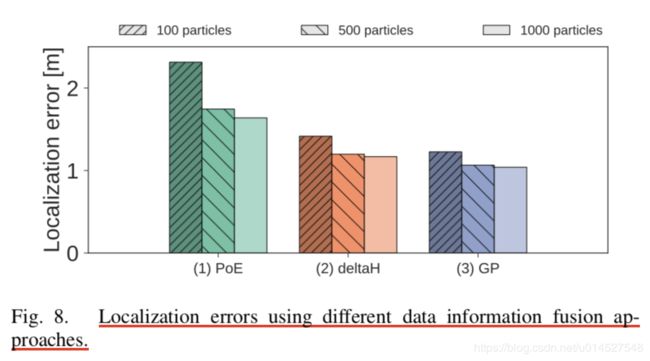
不同融合方法的定位误差:

4. 结论
1) 一般基于wifi进行定位基于各独立概率联合来计算联合概率分布。作者提出一种指数框架的一般点击形式,该框架可以基于各独立概率进行加权计算联合概率分布;
2)引入两种基于信息理论的不需要训练数据的gPoE minH 和 gPoE deltaH方法进行数据融合;
3)为了有效利用训练数据,提出一种基于数据驱动的gPoE GP方法,该方法首先对每个训练数据点计算理想的权重;接着基于高斯过程使用训练数据和对应的理想权重学习一个信号强度和权重的映射关系。
4) 相比于经典PoE模型,gPoE deltaH 和GP都是比较推荐的新方法,当训练时间有限制或者训练数据量有限时比较推荐前者;如果没这样的限制,则推荐使用GP方法,可以获得更好定位性能。