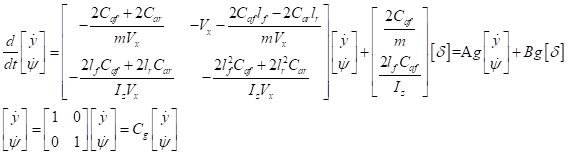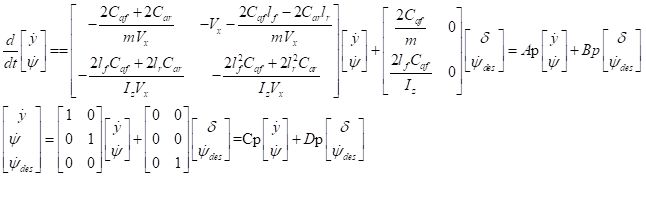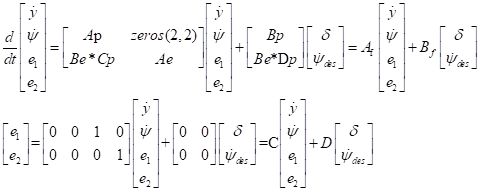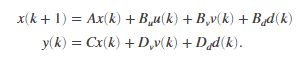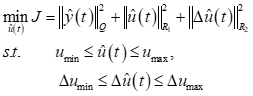基于模型预测控制(MPC)的车道保持控制实现方法
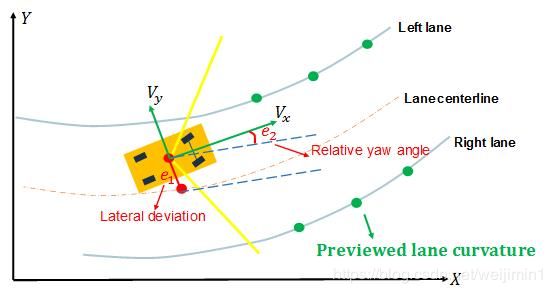
车辆保持的目的是通过检测到车辆与道路中心线的横向偏差和横摆角偏差来控制车辆的方向盘的转角，最终使车辆行驶在道路中心线上。
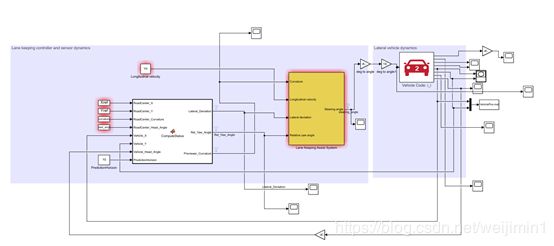
MATLAB 2018b中有一个关于车道保持的案例，本次设计模型控制算法部分与案例相同，但是车辆对象采用Carsim中的车辆模型。整个基于模型预测控制的车道保持系统simulink仿真框架如下所示
图 1
在实际的车辆保持控制算法中可用惯性测量单元IMU测量纵向速度 、横向速度、横向加速度、横摆角速度 等参数。可通过摄像头获取横向偏差，也可以通过摄像头预瞄的点计算出道路的曲率。
车辆的动力学模型
MATLAB 2018b中关于车道保持的案例采用的模型预测控制实现车辆的横向控制,其动力学模型及其推导过程如下
最原始的状态变量为横向距离变化率和横摆角速度变化率
,输入变量车辆的前轮偏角为
。
（1）
将上述公式拓展输出变量为
，输入变量为
新的状态空间方程为
（2）
（3）
将公式（2）带入公式（3）
选取的状态变量
，输入变量为
（4）
注：公式(2)和公式(4)将将期望横摆角的变化率作为输入，实际上期望横摆角的变化率是一个扰动量，在MATLAB2018中输入量和扰动量放在一起，这一点在下一节中也会提到。
MPC的实现
模型预测控制主要包含三大部分:模型预测、滚动优化和反馈矫正。常规的模型预测控制的框架如下所示。
图 2
模型预测
公式(4)为对车辆进行模型预测控制需要的连续车辆横向动力学模型。为了在计算机中实现需要对公式(4)的模型进行离散化，在MATLAB 2018b的getDiscrete函数中采用Simpson's rule 计算
,
，在实际车辆控制中为了实现的方便性建议中采用双积分变换求解具体实现如下所示
，
。
在公式(4)的状态空间方程中，对应的横向偏差及变化率，横摆角偏差及变化率的计算如下所示。
期望的横摆角速度
，车辆实际的偏航角速度
通过IMU测量得到。从而得到横摆角速度偏差
。横摆角偏差通过横摆角速度偏差求积分得到。
横向偏差的变化率
，横向偏差 通过横向偏差的变化率求积分得到。横向偏差和横摆角的偏差如图3所示。实际这么求解横向偏差和偏航角偏差是否有问题？
图3
根据道路中心线的坐标计算出道路中心线曲率的时间序列，根据当前的时间和预瞄的长度，从上述时间序列中取出当前的曲率和预瞄时间内需要的曲率。在Curvature Previewer模块中实现上述功能。
航向角偏差通过本车的航向角、纵向速度、曲率计算得到。期望的航向角计算的方法，期望的航向角为在期望位置的切线与X轴之间的夹角。
如果是双移线工况
可以通过上述公式直接计算出期望的航向角。如果能够事先获得参考轨迹的Xref,Yref坐标则可以通过另外一种方法计算期望航向角，具体如下所示。
DX = gradient(Xref,Ts);
DY = gradient(Yref,Ts);
head_angle = atan2(DY,DX);
Matlab中对应状态空间方程的表示形式，控制量、可测量的扰动，以及不可测量的扰动对应矩阵都是放在B中。
在MPC控制作为模型预测的模型中，期望的航向角速度时作为测量扰动。
获得离散后的车辆状态空间模型后，通过不断的迭代就可以得到模型的预测输出。
在MATLAB 2018b的案例中获得模型预测控制需要的状态空间模型在lkablock_utilGetDiscreteModelForMPC函数实现。
[mpcobj,UseExternalModel,DataType,NumEgoStates,hasLag] = ...
lkablock_MaskInitFcn(gcb,EgoModelMatrixA,EgoModelMatrixB,EgoModelMatrixC,...
MaxSteering,MinSteering,...
InitialLongVel,...
PredictionHorizon,Ts,maxiter,ControllerBehavior,... VehicleMass,VehicleYawInertia,LengthToFront,LengthToRear,FrontTireStiffness,RearTireStiffness,TransportLag);
MPC控制是采用simulink中的Model Predictive Control Toolbox工具箱中的Adaptive MPC Controller模块来实现的。
控制相关的参数如下所示
| 名称 |
值 |
| Ts |
0.1s |
| m |
1575kg |
| Iz |
2875kg.m2 |
| If |
1.2m |
| Ir |
1.6m |
| Cf |
68623 N/rad |
| Cr |
533911 N/rad |
| Np |
10 |
| Nu |
2 |
| R1 |
0 |
| R2 |
0.1/alpha |
| Q |
[1 0.1]/alpha |
| Umax |
0.5rad |
| Umin |
-0.5rad |
滚动优化
得到车辆模型在预测时域内的预测输出后，建立模型预测输出与期望输出之间的偏差和控制量及其变化率的二次型目标函数，具体如下所示。通过二次规划的方法可以求解出最优的控制量即前轮偏角。由于期望的输出是横向偏差和横摆角偏差，所以期望的输出值为0。
通过在每个控制周期不断地求解最优的控制量，形成滚动优化过程。
反馈矫正
反馈矫正是通过比较模型输出与实际对象输出之间的偏差来修正模型的预测输出，这一点在目前的MATLAB 的车道保持案例中暂未体现出来。
MPC 控制参数调节
MPC的控制参数通过Mask->View base mask->Initialization中调用lkablock_MaskInitFcn函数实现的。权重参数、预测时域、控制时域等在lkablock_MaskInitFcn函数中的子函数generateMPC中设置。
整个权重参数的调节是通过一个基本参数beta来调节，其值在0-1之间可调，具体计算如下所示。
weightrange = 50;
alpha =1 /weightrange^(beta-0.5);
控制量变化率的权重为0.1*alpha, 输出偏差的权重为[1 0.1]/Alpha。
当beta往1变大时，alpha变小，控制量变化率的权重系数变小，输出偏差的权重系数变大，控制量变化率变大，控制很激进。当beta往0变小时，alpha变大，控制量变化率的权重系数变大，输出偏差的权重系数变小，控制量变化率变小，控制相对来说变得缓慢。详细的参数调节对应的MATLAB程序如下所示。
% Specify the MPC signal types in the plant.
sys = setmpcsignals(sys,'MV',1,'MD',2);
%% MPC Design
mpc1 = mpc(sys,Ts);
% Specify the prediction horizon.
mpc1.PredictionHorizon = psteps;
% Specify the control horizon.
mpc1.ControlHorizon = round(max(0.1*mpc1.PredictionHorizon,2)); //控制时域
% Specify MV constraints: max/min acceleraion.
mpc1.MV.Min = umin;
mpc1.MV.Max = umax;
% Specify scale factors based on the operating ranges of the variables.
mpc1.MV.ScaleFactor = umax-umin; % range of the steering angle
mpc1.DV.ScaleFactor = 0.01; % scale factor of road yaw angle rate
mpc1.OV(1).ScaleFactor = 0.5; % scale factor of lateral deviation w.r.t road
mpc1.OV(2).ScaleFactor = 0.1; % scale factor of relative yaw angle w.r.t. road
% Specify weights.
alpha = getWeightParam(weightratio); % relating slider on mask to weights in MPC design
mpc1.Weights.MVRate = 0.1*alpha;
mpc1.Weights.OV = [1 0.1]/alpha; % tighter control on lateral deviation over relative yaw angle
ScaleFactor 的作用是在优化的目标函数中将控制量和输出量统一成一样的范围，方便调节输出权重和控制权重。
总结
本文介绍MATLAB的基于MPC的车道保持控制案例的实现过程，并将实际的车辆对象通过Carsim中的车辆仿真对象进行替代，最后重点介绍了MATLAB中关于模型预测控制的参数调节方法。