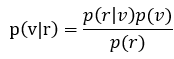卷积码译码之维特比译码算法（Viterbi decoding algorithm）

卷积码译码之维特比译码算法

（Viterbi decoding algorithm）

       本文主要介绍了卷积码的一种译码方法——维特比译码(Viterbi decoding)。

       关键词： 卷积码译码 维特比译码算法 

       卷积码简介：点击打开链接

       ============================================================== 

       目录结构：

       1、维特比译码简介

       2、维特比译码过程

        ==============================================================

1、维特比译码简介

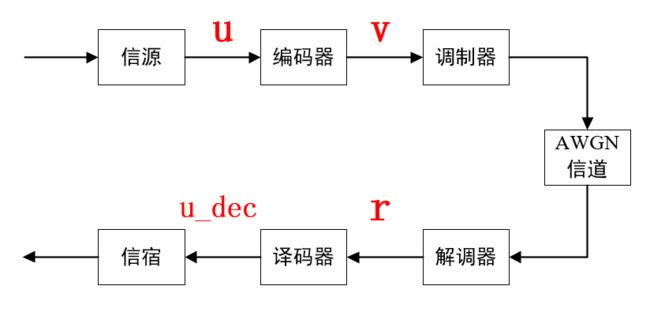
       Viterbi算法是由美国科学家Viterbi在1967年提出的卷积码的概率译码算法，后来学者深入研究中证明Viterbi算法是基于卷积码网格图的最大似然译码算法。何为最大似然译码？在这里我们可以进行以下简单的理解：即根据已经接收到的信息，得到最接近编码码字的一种译码码字。得到这种码字使用的译码准则为最大似然译码。（如果觉得繁琐，第1部分可先略过）
       定义以下信号如图1所示：
       （1）发送端
       信源：u
       编码器输出编码码字：v
       （2）接收端
       译码器输入信息：r
       译码器输出：u_dec

 

图1、经典通信系统

       译码器输出序列u_dec是u的一个估计值。译码器根据一定的译码规则，由接收序列r产生u_dec序列。由于信息序列u与码字v有对应关系，所以等效于译码器产生一个码字v的估值v’。当v‘=v是，u_dec=u。所以，当v‘不等于v时，译码出现错误。
       译码器的条件错误概率定义为：

       译码器的错误概率定义如下：

       其中接收序列r是译码前产生的，所以p(r)与译码规则无关。为了是译码错误概率最小的最佳的译码准则必须满足对所有的r使p(E|r)最小。所以有

       根据以上公式可知，对于给定的接收序列r，如果选择适合的v’，使p(v’=v|r)最大，则一定是最佳的。
根据贝叶斯公式：

       如果发送码字的概率p(v)相同，p(r)又与译码规则无关，则

       所以，译码器如果可以选择一个估计值使得上式最大，则这种译码器称为最大似然译码。p(r|v)称为似然函数。对数似然函数则如下：

       如果码字不是等可能的，最大似然译码不一定是最佳的。在这种情况下，在决定哪个码字能使p(v|r)最大时，必须以概率p(v)对条件概率log p(ri|vi)加权。但在许多系统的接收端不知道发送码字的概率，所以最佳译码是不可能的，最大似然译码就成了可行的译码规则。
       转移概率p<1/2的二进制对此信道（BSC），接收序列r是二元的。对于卷积码，对数似然函数如下：

       其中d(r,v)是r和v之间的汉明距离。由于对所有的v，log p/(1-p) < 0且N log(1-p)是常熟，因此，对于BSC而言，最大似然译码是选择使r和v之间距离最小的v‘作为码字v。

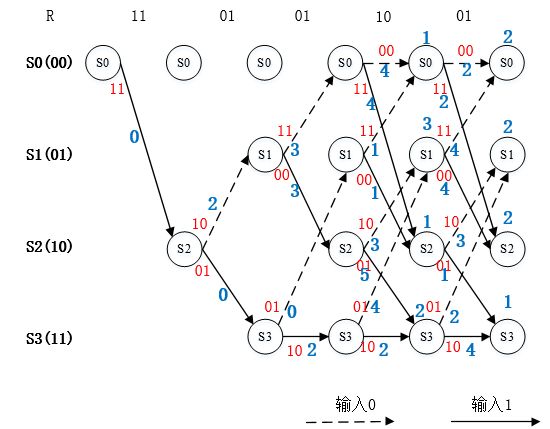
2、维特比译码过程

       由于最大似然译码等效于最小距离译码，因此具有最小d(r,v)累积值的路径就是log p(r|v）的最大路径，该路径被称为幸存路径。定义BM=d(ri,vi)，称为分支度量值。PM称为最小累积度量值，是对所有分支度量值的累积。
       卷积码的编码过程与网格图中的一条路径对应，即输入序列的编码过程与网格图中的路径一一对应。当序列长度为x时，网格中有2^x条不同的路径和编码器的2^x种输入序列对应。在网格图中，每个状态转移的过程中都会输出编码码字。由于译码过程也建立在网格图中，并且从全零状态开始，从全零状态结束。所以，在每个符合输入的分支中，都可以计算出分支度量值。
       维特比译码算法步骤如下：
       （1）在j=L-1个时刻前，计算每一个状态单个路径分支度量。
       （2）第x-1个时刻开始，对进入每一个状态的部分路径进行计算，这样的路径有2^k条，挑选具有最大部分路径值的部分路径为幸存路径，删去进入该状态的其他路径，然后，幸存路径向前延长一个分支。
       （3）重复步骤（2）的计算、比较和判决过程。若输入接收序列长为（x+L-1）k，其中，后L-1段是人为加入的全0段，则译码进行至（x+ L-1）时刻为止。
       若进入某个状态的部分路径中，有两条部分路径值相等，则可以任选其一作为幸存路径。
       该 译码算法的核心思想在于“ 加、比、选”，务必牢记，
        加指的是将每个路径的分支度量进行累积。度量的方法有汉明距或者欧式距离等方法。
        比指的是将到达节点的两条路径进行对比。

       选指的是选出到达节点的两条路径中度量值小的一条路径作为幸存路径。

       

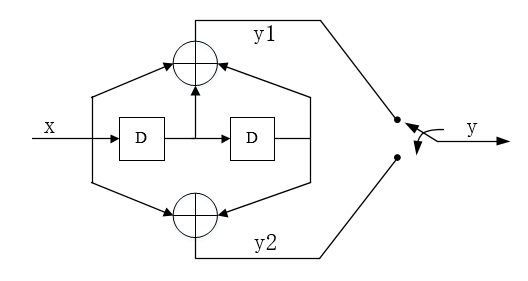
       以（2,1,2）卷积码例子说明维特比译码过程：
       输入数据：u = [1 1 0 1 1]
       编码码字：V = [11 01 01 00 01]
       接收码字：R = [11 01 01 10 01]

       （2,1,2）卷积码在以上算法中的参数，x=5，L=3，k=1，j从0开始计时。

       该卷积码的编码结构如下图所示：

 

图2.（2,1,2）卷积码编码结构图

 

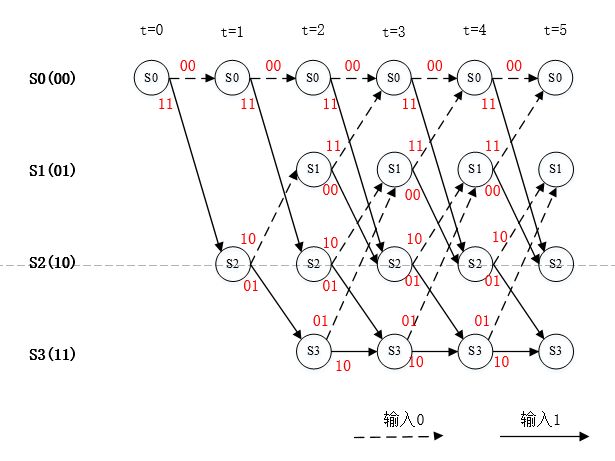
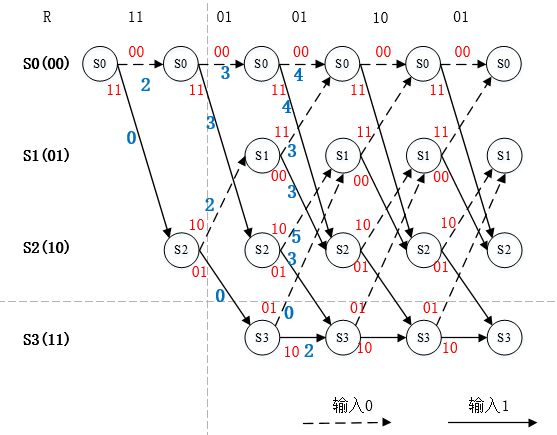
图3. 各个分支的编码输出如图所示

 

图4. 解码步骤1

       解码步骤（1），j=0,1,2这3个时刻中计算出每个路径的分支度量值和，即汉明距离，在图中以蓝色的数字表示。比如接收序列R中的第一个符合“11”，与第一回合的两条路径中的“00”，“11”的汉明距分别为2和0，改数字被标注在每条线对应的下方或附近。
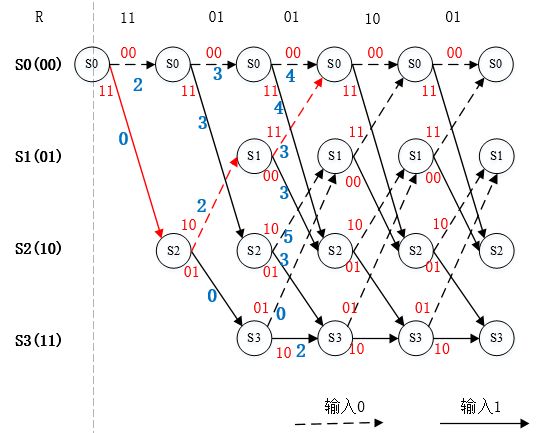
       在每个状态节点具有两条路径时，译码算法才开始根据分支度量的大小选择幸存路径，再删除其他路径。该步骤如下图所示。

 

图5. 第一个节点的幸存路径选择

       图5. 第一个节点的幸存路径选择，由于进入状态S0的两条路径的度量值3<4，所以选择度量值为3的图中红色线为幸存路径。

 

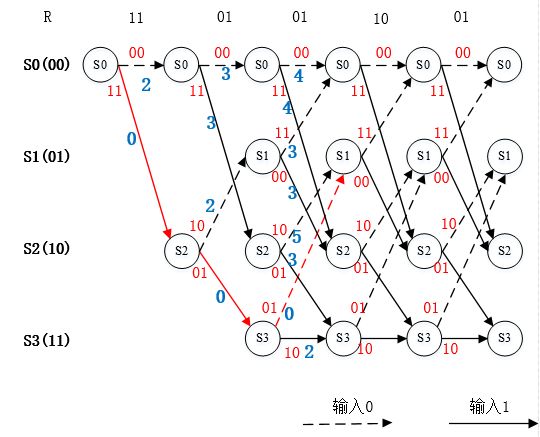
图6. 第二个节点的幸存路径选择

 

图7. 第三个节点的幸存路径选择

 

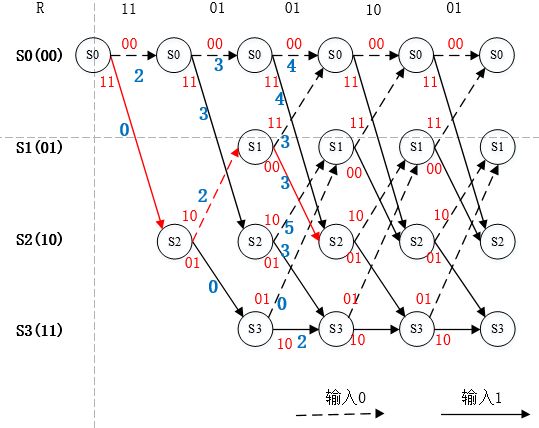
图8. 第四个节点的幸存路径选择

       至此，第一次幸存路径选择完成，现在删除其他路径，将接下来的路径的分支度量值都标注在图中，如下图示。

 

图9. 剩余译码路径的分支度量值计算标注

       以上图中在每个节点进行比较分支度量值比较，胜出的分支度量值被标注在状态节点的上方。
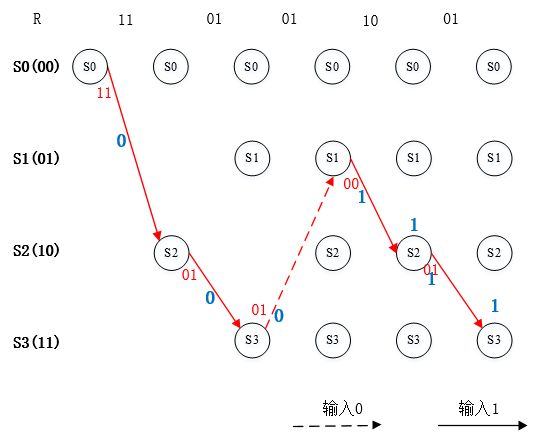
       以上图中在最后一个符号的译码得出一条分支度量值最小的路径，如下图所示，该条路径即译码的最佳路径。

 

图10. 最佳路径输出

       根据该路径得出的译码输出为【11 01 01 00 01】与例子中编码码字V相同。该码字对应的输入数据可以根据以上最佳路径实线或者虚线读出，即【1 1 0 1 1】。

       网格图中的每一条路径的编码输出matlab代码如下所示：

clc;close all;clear
fid = fopen('test.txt','wt');
d1  = 0;
d2  = 0;
N   = 5;
for i = 0:31
    data = dec2bin(i,N);
    for j = 1:N
        %output calculation
        x   = str2num(data(j)); 
        y1  = mod(x + d1 + d2,2);
        y2  = mod(x + d2,2);
        y   = [y1,y2];
        %shift
        d2 = d1;
        d1 = x;
        fprintf(fid,'%d%d ',y1,y2);
    end
    fprintf(fid,' %s\n',dec2bin(i,5));
    d1 = 0;
    d2 = 0;
end
fclose('all')