随机数发生器设计原理及实现

 随机数发生器设计原理及实现

作者：不赖猴  内核编程和密码学群：20264887

 

随机数是密码学算法的基础，是现代加密体系中最重要的部分之一。几乎所有的密码学算法都需要使用随机数。那么是否真的存在真正的随机数呢？这个问题已经讨论了很多年，我们这里就不论述了，我们只需要知道量子力学已经证明在现实世界中随机数是真实存在的。

 

1.       什么是随机数发生器？

 

定义：一个随机数发生器就是一个产生数据流的设备，数据流中的每一位都是不可预测，偶然的。但是从一定长度的数据流来看，它又符合某种分布。

从定义上看，随机数发生器具备以下三个属性：

                         i.              看起来具备随机性。

                       ii.              不可预测性。

                      iii.              不能被可靠的重复产生。

 

大多数编译器都已嵌入了随机数生成器，但是这些随机数发生器对密码来说几乎肯定是不安全的，甚至他们中的大部分产生的是非常差的随机数。通常应用中对随机数有两个不同的并且不一定相容的要求：随机程度和不可预测程度。

 

l         随机程度：通常在产生的一系列声称是随机的数值时，我们关心的是这些数值在某种统计意义上是随机的。即均匀分布和独立性。

l         不可预测程度：对于“真正的”随机序列，每个数与序列中的其他数都是统计独立的，因此不可预测。然而，实际上我们很少能使用到真正的随机数；相反我们用到的都是由某种算法生成的。这个时候，我们得防止攻击者从序列前边的元素预测出将来的元素。

 

2.       随机数发生器的分类。

 

一般来说，随机数发生器有三种，它们分别是真随机数发生器(TRNG，True Random Number Generator)、伪随机数发生器(PRNG，Pseudo Random Number Generator)和密码学安全随机数发生器(CSPRNG，Cryptographically Secure Pseudo Random Number Generator)。

                         i.              TRNG生成的是真正的随机数，但是真正的随机数的来源难以得到。物理的噪声发生器，比如离子辐射事件的脉冲检测器、气体放电管和带泄露的电容，是一个可能的来源。还有电脑的硬件中断、定时器偏差等。

                       ii.              PRNG是通过某一种确定性算法来生成随机数。它们并不是真正的随机数，而是看起来是随机的。即可以通过我们所能找到的所有随机性统计检验。由于这些数字有可重复性，所以它们是伪随机的。很多编译器都提供了自带的PRNG，比如C/C++的rand()和Object Pascal的random()等等。

                      iii.              CSPRNG除了具备PRNG的属性外，还具备一些密码学要求的属性。它经常被用于以下几个方面：

1.         随机密钥的产生。比如为对称密码算法加密提供随机密钥。

2.         一次性随机序列的产生。比如用于通信协议，可以防止回放攻击。

3.         用于口令保护的盐渍(salt)的产生。可以防止口令的预计算攻击（也叫字典攻击）。

4.         一次一密。比如直接拿来跟明文异或生成密文，但是只能用一次。

 

下图说明了三种随机数发生器的区别。

 

3.       密码学安全的随机数发生器(CSPRNG)的设计原理。

 

从应用角度看，CSPRNG通常分为基于开发平台的CSPRNG和不基于开发平台的CSPRNG。基于开发平台的CSPRNG比如有Linux和Windows内核所带的随机数发生器。不基于开发平台的CSPRNG则有很多，比如适用于短运行时的Yarrow PRNG、INST的基于散列算法的DRBG函数和适用于长运行时的Fortuna PRNG等等。值得注意的是，基于开发平台的CSPRNG主要用于为不基于开发平台的CSPRNG提供初始化种子。因为基于开发平台的CSPRNG由于可能阻塞的原因，并不适合需要快速提供熵源的密码学应用。而不基于平台的CSPRNG可以提供比基于平台的CSPRNG快的多的熵源。

 

3.1 基于开发平台的CSPRNG设计原理。

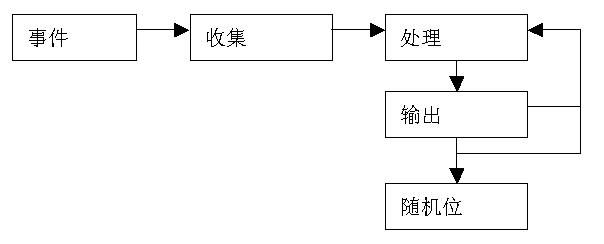
实际应用中，基于开发平台的CSPRNG都是围绕某些事件收集处理机制进行的。如下图所示。

 

 

 

3.1.1 事件

 

在通常的情况下，产生随机数的最好办法就是找出许多似乎是随机的事件，然后从中提取随机性，也就是熵。如果随机数发生器(RNG，Random Number Generator)试图从某个事件中提取熵，那么这个事件就是一个RNG事件。它们是系统中不以高度可预测的时间间隔或者状态而发生的事件。RNG的目的就是捕捉这个事件，收集可用的熵并将它传递给RNG内部状态进行处理。

事件以各种形态和大小发生。一个RNG使用什么样的事件高度取决于正在开发的是什么平台。比如以下这些事件：

l         硬件中断。以下三个来源每一个只有很少的熵，但是将它们结合在一起就会有足够多的非零熵。

                         i.              来自定时器中断的熵。

                       ii.              和事件相关联的数据，比如键盘中断，鼠标中断等等。

                      iii.              具有很高分辨率的自由运行的计数器的捕捉。比如，在x86处理器中，RDTSC指令可以用来捕捉计数器。

l         定时器偏差

l         模数转换错误

 

3.1.2 收集

 

现在我们知道可以从一些源中得到熵，那么我们就必须设计一种能够快速收集它们的方法。收集处理这一步的目标是为了减少事件的延迟时间，因为中断处理程序的延迟时间必须足够小以确保系统的性能。这样，中断就可以在一个合理的可控的时间内运行。收集一般需要两个步骤。

第一步：拥有一块预分配好的内存，用来存储从事件中获取的数据。但是会引入一个问题。内存块大小是一定的，当块满了后，要么忽略新的输入，要么把已满的丢掉，这样会导致丢掉新的（或者更旧）的事件来确保缓冲区没有溢出。但是这会给攻击者留下一个缺口，一个知道熵可以被丢弃的攻击者可能会触发一系列低熵事件来确保收集到的数据的质量很差。为了解决这个问题，我们必须在攻击者触发一系列低熵事件后，不丢弃任何熵，而是把这些熵逐步累积达到高质量的数据，这就是第二步要做的，当然这要求内存块的大小应该满足允许我们收集足够多的熵。

 

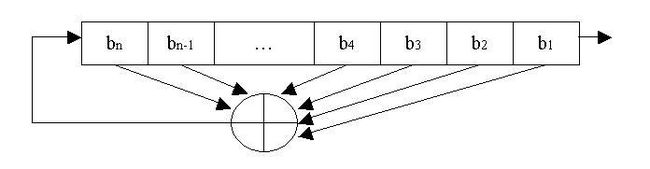
第二步：将熵和一个可以保留熵的线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)进行混合。一个LFSR实际上是一个PRNG装置，它把内部状态的线性组合作为输出(如下图)。基本的LFSR是由一个n位的寄存器组成，它移动一次并将移出的为和移位寄存器中选择的位进行异或。这些被选择的位称为“tap位”,也叫抽头序列。一个n位LFSR能够处于2^n-1个内部状态中的一个。这意味着，理论上，n位LFSR在重复之前能够产生2^n-1位长的伪随机序列。只有具备一定抽头序列的LFSR才能循环地通过所有2^n-1个内部状态。而这个抽头序列加上常数1形成的多项式必须是本原多项式模2。

 

 

 

<1>. 基本的LFSR方式。

为了将收集到的熵与LFSR混合，我们与使用自身的线性组合来修改LFSR内部状态不同的是，它们将内部的位和事件中收集到的位相异或。因为LFSR是熵保留的，对于常用的32位LFSR，不管提供多少种子位，这个结构最多在状态中产生32位的熵，但是这远远不能满足任何密码学的需求，它必须被加到一个更大的缓冲池之中。

 

<2>. 基于表的LFSR。

当增加一些字节时，用一次一位的时钟控制LFSR是一种很慢的操作。作为中断来运行，是非常慢的方式。为了加快处理速度，我们可以采用查找表的方式一次处理一个字节，而不是象基本的LFSR那样一次只处理一位。同样，最后产生的熵必须被加到一个更大的缓冲池之中。

 

3.1.3 处理和输入

 

CSPRNG处理步骤的目的是将收集的种子数据转化为某些可以返回给调用函数的东西，同时不影响CSPRNG内部状态。如果这里只是简单用一个调用函数来处理的话，那么提供随机数是不安全的。因为大部分情况下，缓冲池的熵总是小于缓冲池的大小。这就为推断LFSR内部状态提供了可能。

处理的一般技巧是使用一个单向散列函数来处理种子数据并将它同CSPRNG内部的状态“搅拌”在一起。但是，这里有一个问题需要解决。由于从平台上收集的事件可能是阻塞性的，也就是说在某些时刻，LFSR没有被更新。这个时候，我们要么等待新的事件种子的收集，要么使用旧的种子。但是这两个选择对我们来说都是不可取的。为了解决这个问题，我们采用普通PRNG的方式。当LFSR没有被更新时，我们并不等待新的事件种子，而是简单地重新搅拌当前的状态、缓冲池以及搅拌计数器。 该搅拌计数器确保了每次搅拌时散列的输入都是唯一的。

 

3.1.4 存在的问题

 

大部分平台都会面临一个问题，就是第一次启动的时是缺乏熵的，因为不可能收集足够的事件。一般的解决方法是在系统关闭前在磁盘上创建一个种子文件以便下次启动时使用。但是这存在安全隐患。因为如果在种子文件被删除之前攻击者可以读取它的话，那么RNG中所有的熵都有可能暴露给攻击者。虽然有一些方法可以在一定程度上阻止攻击者获取这个种子文件，却不能根除存在的安全隐患。唯一可靠的方法就是在系统启动之后和调用RNG之前，等待足够多的随机事件发生。

 

3.2 不基于开发平台的CSPRNG设计原理。

 

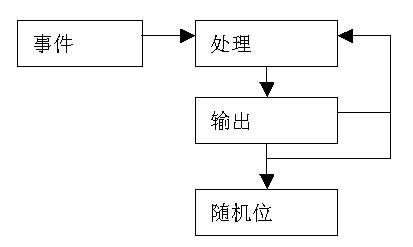
不基于开发平台的CSPRNG的处理流程同基于开发平台的CSPRNG很相似(如下图)。不同的是不需要收集这一步。任何输入的熵都是直接送给处理层并且马上成为CSPRNG的状态的一部分。正是这个原因，不基于开发平台的CSPRNG要比基于开发平台的CSPRNG快的多，且不存在阻塞的情况。

 

 

 

根据应用的不同，不基于开发平台的CSPRNG可以分为两类。对于许多短运行时间的应用程序来说，例如文件加密工具，CSPRNG必须以短的时间周期生存并且还要对输出的长度不敏感。对于长的运行时间的应用程序来说，例如服务器和用户守护程序，CSPRNG要有长的生命周期并且必须合理的维护。

与基于开发平台的CSPRNG不同，不基于开发平台的CSPRNG有很多公开的成熟的算法，比如Yarrow PRNG、Fortuna PRNG、ANSI X9.17 PRNG和Blum Blum Shub PRNG等。这里就不细加说明了。

 

4.       密码学安全的随机数发生器(CSPRNG)的实现。

 

这一节主要论述基于开发平台的CSPRNG的实现，至于不基于开发平台的CSPRNG，有很多公开的成熟的算法实现。下面所提及的CSPRNG都是基于开发平台的CSPRNG。一般的开发平台都会提供自带的内核级的CSPRNG，比如Windows内核实现的CSPRNG就可以用它提供的CryptGenRandom这个API来获得输出。但是Windows没有公开其实现的细节。这里我们就参照Linux内核提供的CSPRNG来看一下它是怎么实现的。

 

4.1 事件的捕获

 

第3节我们提到开发平台提供了很多随机事件让我们去捕获。 这里我们并不去深入讨论这些事件，在x86世界中，已证实至少有一种足够有用（虽然很慢）的来源，即使用RDTSC指令来获取高分辨率自由计数器的读数来作为种子数据。以下是具体的步骤及代码。

<1>. 检查当前的平台是否支持获取CPUID.

function _CheckCPUID: boolean; assembler;

asm

  pushfd

  pushfd

  pop      eax

  mov      ecx,eax

  xor      eax,$200000

  push     eax

  popfd

  pushfd

  pop      eax

  popfd

  xor      eax,ecx

  setnz    al

end;

<2>.如果支持获取CPUID,则检查当前平台是否支持RDTSC指令。

function _CheckRDTSC: boolean; assembler;

asm

  push   ebx

  mov    eax,1

  db     $0f,$a2          {cpuid}

  test    dx,$10           {test RDTSC flag in Features}

  setnz   al

  pop    ebx

end;

<3>.如果支持RDTSC指令，则使用RDTSC指令提取种子数据。

因为这个高分辨率自由计数器是64位的，所以定义了一个结构TctrRec来记录捕获的读数。

TCtrRec = packed record

    LDW, HDW: longint;

end;               

 

procedure _RDTSC(var Ctr: TCtrRec);

begin

  asm

    push  ebx

    xor   eax, eax

    xor   ebx, ebx

    xor   ecx, ecx

    xor   edx, edx

    db    $0f,$a2    {cpuid}

    db    $0f,$31    {rdtsc}

    mov   ecx,[Ctr]

    mov   [ecx],eax

    mov   [ecx+4],edx

    xor   eax, eax

    db    $0f,$a2    {cpuid}

    pop   ebx

  end;

end;

 

4.2 收集事件

 

<1>. 使用一个32位的LFSR收集事件。

 

我们设计一个32位的LFSR，它的抽头序列为0x800000C5。

function Lfsr(state: DWORD):DWORD;

begin

 if (state and $00000001) = $00000001 then

  result := (state shr 1) xor $800000c5

 else

  result := state shr 1;

end;

 

然后我们将收集到的熵与之混合。

function FeedLfsr(state: DWORD; seed_bit : integer):DWORD;

begin

 state := state xor seed_bit;

 result := Lfsr(state);

end;

 

测试代码，这里假设保存事件的内存块大小为64个字节。

procedure TForm1.Button1Click(Sender: TObject);

var

 i      : integer;

 buf    : TCtrRec;

 aState : DWORD;

begin

 _RDTSC (buf);      // 利用RDTSC指令读取计数器的值.

 for i:=0 to 63 do     // 一次一位的处理

 begin

  case (i div 32) of

   0:  aState := FeedLfsr(aState,(buf.LDW shr i) and $00000001);

   1:  aState := FeedLfsr(aState,(buf.HDW shr i) and $00000001);

  end;

 end;

 Showmessage(format('%x',[aState]));

end;

用来收集熵的内存块中的每一位(seed_bit,要么为1，要么为0)都会调用FeedLfsr这个函数，直到内存块为空。由于这种方式的LFSR是一个时钟一位的处理，速度太慢。为了提高速度，我们采取查表的LFSR方式。

 

<2>. 基于表的LFSR。

 

对于一个32位的LFSR，可以有256个不同的初始状态。由于其抽头序列是本原多项式模2，所以移位和抽头序列异或后可以生成256个不同的内部状态。一个8位的种子数据所表示的值可以作为索引被用来选择LFSR的256个内部状态中的某一个。这样我们可以一次处理一个字节的种子数据。它等效于调用8回一次一位的LFSR。

8位的查找表大小为256项32位状态，总大小为1K字节。创建这个查找表的代码如下：

var

 shiftab : array[0..255] of DWORD;

 

function Step_one(state : DWORD):DWORD;

begin

 if (state and $00000001) = $00000001 then

  result := (state shr 1) xor $800000c5

 else

  result := state shr 1;

end;

 

procedure Make_tab;

var

 x,y,state : DWORD;

begin

 for x:=0 to 255 do

 begin

  state := x;

  for y:=0 to 7 do

  begin

   state := Step_one(state);

  end;

  shiftab[x] := state;

 end;

end;

 

一次混合一个字节熵的代码如下：

function Step_eight(state : DWORD):DWORD;

begin

 result := (state shr 8) xor shiftab[state and $ff];

end;

 

function Feed_eight(state: DWORD; seed : byte): DWORD;

begin

 state := state xor seed;

 result := Step_eight(state);

end;

 

测试代码，这里假设保存事件的内存块大小为64个字节。

procedure TForm1.Button3Click(Sender: TObject);

var

 i      : integer;

 buf    : TCtrRec;

 aState : DWORD;

begin

 _ReadCounter(buf);      // 利用RDTSC指令读取计数器的值.

 make_tab;              // 创建查找表.

 for i:=0 to (63 div 8) do   // 一次一个字节的处理

 begin

  case ((i*8) div 32) of

   0:  aState := feed_eight(aState,(buf.LDW shr i*8) and $000000FF);

   1:  aState := feed_eight(aState,(buf.HDW shr i*8) and $000000FF);

  end;

 end;

 Showmessage(format('%x',[aState]));

end;

 

<2>. 实际的事件收集方式。

 

实际上，对事件的收集是运行在平台内核里的。一旦平台启动，就会开始收集各种事件的熵。比如，为了收集键盘事件，我们把事件收集函数放在键盘的中断处理列程里调用；为了收集鼠标事件，我们把事件收集函数放在鼠标的中断处理列程里调用。因为我们这里收集的是自由运行的计数器的读数，所以我们可以用一个线程来模拟。使用这个CSPRNG的应用程序一启动，这个收集线程就开始自动收集自由运行的计数器的读数。虽然这样收集事件的熵有些慢，但是如果只是为不基于平台的CSPRNG提供初始化种子的话，已经足够了。

这里我们采用基于查表方式的LFSR，收集事件的函数为：

procedure RNG_Add_Byte(seed : byte; entropy : DWORD);

begin

  {用基于查表法的LFSR收集种子，每次一个字节}

  aLFSR := aLFSR xor Seed;

  aLFSR := (aLFSR shr 8) xor shiftab[aLFSR and $FF];

  { bit_count为熵的累积，当累积的熵超过32位后，即收集满一个32位的LFSR后，}

  {将LFSR跟8个32位字的CSPRNG的内部状态缓冲池的一个32位字异或.        }

  bit_count := bit_count + entropy;

  if (bit_count >= (32 shl 4)) then

  begin

    rngState[word_count and $7] := rngState[word_count and $7] xor aLFSR;

    word_count := word_count + 1;

    bit_count := 0;

  end;

end;

需要提示的有以下几点：

l         由于熵的值可能含有小数部分，比如在英语文本中，英文字母平均含有1.3位的熵。在累积熵的时候，为了把熵的小数部分也累积进去，就需要采用含有小数的编码。这里的bit_count是采用.4小数编码法。就是说，一个32位的bit_count，高28位是其整数部分，低4位为小数部分。例如bit_count = 0x00000011就表示bit_count累积的熵为1+1/16=1.0625位熵。同样，函数的输入值entropy采用的是同样的编码方式。

l         word_count是用来累积当前有多少个32位字被LFSR更新过。这里我们采用的CSPRNG内部处理缓冲池是8个32位字。

这里我们估计通过RDTSC指令获取的自由运行计数器的每个字节的熵为1/16位。则在线程中我们按以下方式调用：

RNG_Add_Byte((_RDTSC.LDW and $FF), 1);

RNG_Add_Byte(((_RDTSC.LDW shr 8) and $FF), 1);

RNG_Add_Byte((_RDTSC.HDW and $FF), 1);

RNG_Add_Byte(((_RDTSC.HDW shr 8) and $FF), 1);

 

4.3 处理和输出

 

我们选择SHA-256来对收集到的种子数据进行搅拌。由于SHA-256的输出实际上是8个32位字。所以搅拌缓冲区也是256位。

procedure STORE32L(x: DWORD; y: PByte);

begin

  PByte(y)^ := x and $FF;

  PByte(DWORD(y)+1)^ := (x shr 8) and $FF;

  PByte(DWORD(y)+2)^ := (x shr 16) and $FF;

  PByte(DWORD(y)+3)^ := (x shr 24) and $FF;

end;

 

procedure LOAD32L(x: DWORD; y: PByte);

begin

  x := (PByte(y)^ and $FF) or ((PByte(DWORD(y)+1)^ and $FF) shl 8) or ((PByte(DWORD(y)+2)^ and $FF) shl 16) or ((PByte(DWORD(y)+3)^ and $FF) shl 24);

end;

 

procedure RNG_Churn_Data;

var

 buf : array[0..63] of byte;

 x,y : DWORD;

begin

  {为了防止LFSR事件收集阻塞，先用搅拌计数器跟内部状态的第一个32位字进行异或}

rngState[0] := rngState[0] xor churn_count; 

  churn_count := churn_count + 1;

  {将8个32位字按little endian格式储存到256位的搅拌缓冲池中}

  for x := 0 to 7 do

  begin

   STORE32L(rngState[x],@buf[(x shl 3)]);

  end;

  {用SHA256对缓冲池内的55个字节进行搅拌。只选择搅拌55个字节而不是全部的64}

  {个字节纯粹是为了提高效率，因为SHA256每次填充的消息长度只有55个字节，如果}

  {要处理64个字节的话，需要填充两次。                                        }

  SHA256Full(pool,@buf[0],55);

  {将搅拌完后的256位缓冲池按little endian格式加载到8个32位字的内部状态中去,   }

  {并与原来的状态进行异或后保存,这样可以防止回溯攻击。                         }

  for x:=0 to 7 do

  begin

   LOAD32L(y,@pool[(x shl 3)]);

   rngState[x] := rngState[x] xor y;

  end;

  pool_len := 32;

  pool_idx := 0;

  word_count := 0;

end;

 

搅拌后的数据只有256位，我们需要把它们放到更大的缓冲池中去。

{rngBuf : 更大的随机数缓冲区指针；                                  }

{rngLen : 缓冲区大小；                                              }

{isBlock: 是否采用阻塞方式，如果True的话，在阻塞发生的时候立即返回。}

{        如果False的话，在阻塞发生的时候不返回，只是依靠搅拌计数器 }

{        的累积来获得随机数输出。                                   }

{返回值：返回值为当前已经获得的随机数的字节数。                     }

function RNG_Read(rngBuf : PByte; rngLen: Cardinal; isBlock: boolean):Cardinal;

var

  x,y : Cardinal;

begin

  x := 0;

  while(rngLen > 0) do

  begin

    if (pool_len >0) then

    begin

      for y:=0 to pool_len - 1 do

      begin

        if y < rngLen then

        begin

          PByte(DWORD(rngBuf)+y)^ := pool[pool_idx];

          pool_idx := pool_idx + 1;

        end;

      end;

      pool_len := pool_len -  y;

      rngLen   := rngLen - y;

      x        := x + y;

    end

    else

    begin

      if (word_count >=8) or (not isBlock) then

        RNG_Churn_Data

      else

      begin

        result := x;

        exit;

      end;

    end;

  end;

  result := x;

end;

 

4.4 完整的实现

 

<1>. 生成两个线程，一个线程TfeedThread用来在后台收集事件；一个线程TpoolThread用来将收集到的熵处理后，放到一个大的缓冲池里。

<2>. 根据所需要的随机数的大小，从缓冲池里取出返回给调用者。同时，再次刷新缓冲池里的随机数。

<3>. 同时实现调用Windows内核实现的CSPRNG。

<4>. 根据需要采用自己的CSPRNG和Windows内核的CSPRNG。

 

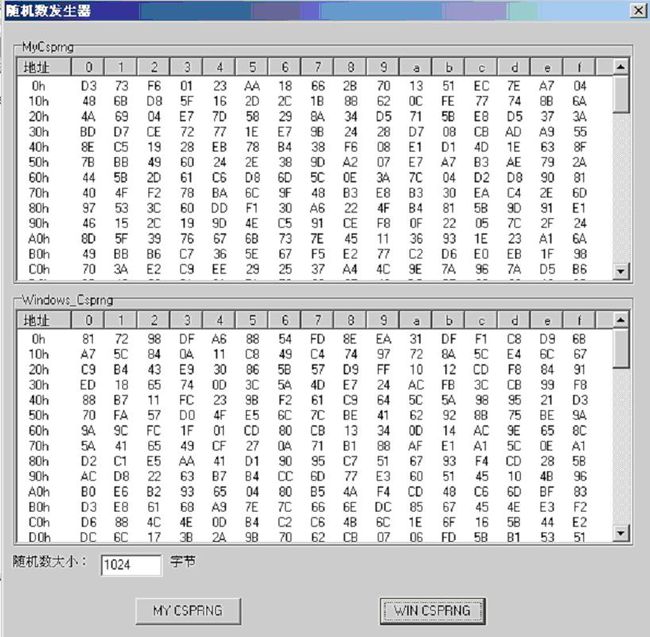
以下是程序截图。

 

 

 

由于我们采用后台线程来收集事件，而且事件也比较单一。每次收集的熵比较少。所以，随机发生器的速度相对比较慢。而Windows内核的CSPRNG由于在内核中收集事件，每次收集的熵比较多。速度相对比较快。而且它收集的熵来源于：

①     当前进程的ID；

②     当前线程的ID；

③     系统引导以来的时钟数；

④     各种高精度的性能计数器；

⑤     用户环境模块的MD4（Message Digest 4，信息摘要4）散列，包括用户名，计算机名和搜索路径等；

⑥     高精度的内部CPU计算器，如RDISC,ROMSR,RDPM等；

⑦底层系统信息，如空闲时间，内检时刻，中断时间，提交限定，页面计数，缓存计数，操作系统外部计数等。

 

 

5.       总结

在设计一个加密系统时首先要解决的是针对生成随机位的问题，这时候，你就需要知道你应该设计或使用一个什么的随机数发生器。下面是一些随机数发生器适应的场合分类。

随机数发生器	适用场合
上述设计的CSPRNG	提供种子，提供盐渍(salt)
Win内核的CSPRNG	提供种子，提供盐渍(salt)
Yarrow CSPRNG	短生命周期的任务，比如文件加密等
Fortuna CSPRNG	长生命周期的任务，比如服务器守护程序
ANSI X9.17 CSPRNG	对称/非对称密钥生成
ANSI X9.31 CSPRNG	对称/非对称密钥生成

 

6.       源代码下载地址：

http://d.download.csdn.net/down/1100881/A00553344