浅谈概率与数学期望
由于鄙人水平有限,故只能给出一些基本的概率入门知识,以及做一些解释,并对一些基础题目诸如三门问题及醉鬼问题的推理。
浅谈概率
先由一道十分经典之题目承题:
三门问题
即有三扇门,有一扇门后由一辆车,另外两扇门分别有一只羊,此时你打开哪扇门,门里的东西就是你的(当然车的价值比羊大且你并不知道每扇门的后面有什么)。此时你已选择了一扇门,但是有知道门后面分别是什么的人给你打开了一扇门后面是羊的门,并给你了一次是否换选择的门机会。
求此时不换门与换门分别的得到车的概率。
我刚看到这道题的时候第一反应就是二分之一啊,因为无论如何此时换与不换都是二分之一概率,其实不然。
分情况讨论,
我们把门分成 123 1 2 3 123,并假设 1 1 1门后面的是车。
情况一:你选了 1 1 1号门,那么你此时不换得到车的概率是100%,而换了的概率是0%
情况二:你选了 2 2 2号门,那么你此时换了得到车的概率是100%,而不换的概率是0%
情况三:你选了 3 3 3号门,那么你此时换了得到车的概率是100%,而不换的概率是0%
所以总而言之,不换能赢得概率是33%(三分之一),换了赢的概率是66%(三分之二)。
如果还不懂的话看下面这个视频(虽然讲的和上面差不多,但总归是生动形象一些)
劳斯莱斯和羊
到这里你应该是懂了这道题的理论,也许你会觉得这也只是理论而已,然而这个答案是经过实验证明的。
1.例如根据福尔曼大学的埃勒维兹·鲁迪的反馈,因为数学课上的大部分老师认为莎凡特是错误的。于是25名老师带着学生们去中学做了大量实验,得到了1480个样本,最后却证明了莎凡特是正确的,即应该换门。
The teachers in my graduate-level mathematics classes, most of whom thought you were wrong, conducted your experiment as a class project. Each of the twenty-five teachers had students in their middle or high school classes play at least 400 games. In all, we had 14,800 samples of the experiment, and we’re convinced that you were correct—the contestant should switch!Eloise Rudy, Furman University,Greenville, South Carolina
2.虽然上个世纪七十年代,电脑和模拟仿真都是稀罕物。但随后,麻省理工的数学家和阿拉莫斯国家实验室的程序员都宣布,他们用计算机进行模拟实验的结果,支持了莎凡特的答案。
3.时隔三十多年后,著名节目《流言终结者》也做实验,一是由于该问题的反直觉,即使时隔多年,照样有人会感到困惑,其次是杰米和亚当这对好基友,再次强有力的印证了莎凡特的答案。
好了,关于三门问题的探讨到此为止,那么接下来我们进入概率的领域,而待会儿我会用概率方面的知识来解决上面这道题。
了解一些基础知识:
基础知识





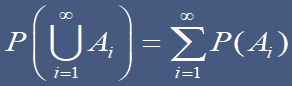

咦,我好像吧ppt抄了一遍,诶懒的打。。。
到此先把以上知识落实一下
先给一道概率的性质应用题:
从无限的1—9中任意取出一些数,取n次,求出这些数的乘积能被10整除的概率
解:
首先能被10整除,那么肯定包括了5或者某一个偶数
那么设取到5这个事件为A,取到偶数这个事件为B,
那么要求的答案就是P(AB)了
P(AB)=1-P(A(加一个上划线)UB(加一个上划线))
就是说,AB都成立的概率,即是1-A的逆事件和B的逆事件的和,就是没有取到5或者偶数或者都没取到
再有容斥原理得
P(AB)=1-P(A(加一个上划线)UB(加一个上划线))=1-P(A(加一个上划线))-P(B(加一个上划线))+P(A(加一个上划线)UB(加一个上划线))=1-( 8 n 8^n 8n+ 5 n 5^n 5n- 4 n 4^n 4n)/ 9 n 9^n 9n
到此为止。
接下来介绍条件概率:
条件概率
设E为一试验,A和B为E中两事件,
且 P(A)>0,则称P(AB)/P(A)为事件A发生的条件下事件B发生的条件概率,
记作P(B|A),即P(B|A)= P(AB)/P(A)
乘法定理:P(AB)=P(B|A)*P(A)=P(A|B)*P(B)
这个公式如何理解呢?
假设我们求学校中哪些小姑娘穿小裙子的概率
那么设学校中的人是小姑娘事件是A,哪些人穿了小裙子是B
**那么作为基数的是小姑娘(也就是在事件A发生的条件下)**这个你要先理解,所以P(B|A)= P(AB)/P(A),而不是P(B|A)= P(AB)。
例题:
布袋里有2颗蓝色球和3颗红色球。每次随机冲布袋里拿一颗,且不放回。在第1次取到蓝球的条件下,第2次拿到蓝球的概率是多少?
解:
定义事件A:先取到一个蓝球(不放回)
事件B:再取到一个蓝球
事件AB:先后两次摸到蓝球
P ( A B ) = 2 / 5 , P ( A B ) = 1 / ( C 5 2 ) P(AB)=2/5, P(AB)=1/(C_5^2 ) P(AB)=2/5,P(AB)=1/(C52)
P ( B / A ) = ( P ( A B ) ) / ( P ( A ) ) = ( 1 / 10 ) / ( 2 / 5 ) = 1 / 4 P(B/A)=(P(AB))/(P(A))=(1/10)/(2/5)=1/4 P(B/A)=(P(AB))/(P(A))=(1/10)/(2/5)=1/4
当然你要用决策树我也没什么意见(概率专题啊喂,毕竟我水平有限,难的概率题还不会……)……
全概率公式
定义 设试验E的样本空间为Ω,事件A1,A2,……,An满足:
1.两两互不相容
2.ΣAi= Ω
3. P(Ai)>0
则称A1,A2,……,An 为 Ω 的一个划分(分割)
定理 设 Ω为试验 E 的样本空间,A 为 E 的一个随机事件,B1,B2,……,Bn 为Ω的一个划分,且有 P(Bi)>0,则

证明:
太惨了我markdown的公式语言不会用于是我……
全概率怎么理解呢(嘻嘻嘻嘻)
譬如有一个小姑娘,她今天可能会穿裙子(概率为0.5),也可能会穿裤子(0.4),也可能会cosplay(0.1),然后她穿裙子能让你心神荡漾的概率是(0.7),穿裤子能让你心神荡漾的概率是(0.9),cosplay能让你心神荡漾的概率是(1),那么请求出这个姑娘今天能让你心神荡漾的概率是多少?
首先我们可以得出 这个姑娘是一个腿又细又长身材很好且很好看的姑娘(哈哈哈哈)
那么设成功的概率是P©
P ( C ) = P ( Q ( 穿 裙 子 的 概 率 ) ) ∗ P ( C Q ( 穿 裙 子 成 功 的 概 率 , 后 面 以 此 类 推 ) ) + P ( K ) ∗ P ( C K ) + P ( C O ) ∗ P ( C C O ) P(C)=P(Q(穿裙子的概率))*P(CQ(穿裙子成功的概率,后面以此类推))+P(K)*P(CK)+P(CO)*P(CCO) P(C)=P(Q(穿裙子的概率))∗P(CQ(穿裙子成功的概率,后面以此类推))+P(K)∗P(CK)+P(CO)∗P(CCO)
也就是成功的概率是由她所有(穿什么的概率乘上好看的概率)的和
也就是P©=0.50.7+0.40.9+0.1=0.81
Yeah!
例题:
例3:袋中有5个球,2个黑球,3个白球,依次取两球,求第二次取到黑球的概率
解:
设B1表示“第一次取到黑球”的事件,B2表示“第一次取到白球”的事件,A 表示事件“第二次取黑球”
由全概率公式,有
P ( A ) = P ( B 1 ) ∗ ( P ( A ∣ B 1 ) ) + P ( B 2 ) ∗ P ( A ∣ B 2 ) = 0.4 ∗ 0.25 + 0.6 ∗ 0.5 = 0.4 P(A)=P(B1)*(P(A|B1))+P(B2)*P(A|B2)=0.4*0.25+0.6*0.5=0.4 P(A)=P(B1)∗(P(A∣B1))+P(B2)∗P(A∣B2)=0.4∗0.25+0.6∗0.5=0.4
(当然决策树也没问题……)
贝叶斯(Bayes)公式
设Ω为E的样本空间,A为E的事件,B1,B2,……,Bn互不相容,且P(A)>0,P(Bi)>0,则:
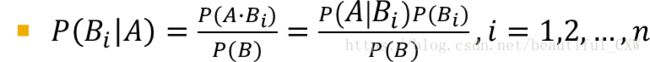
用上面的例子来表现它和全概率公式的不同之处:
请求出这个姑娘穿裤子让你心神荡漾的概率有多大?
!
不要以为是穿裤子的概率和其的积
这个的基事件是(让你心神荡漾)
所以是穿裤子成功的概率除以全部能够让你心神荡漾的概率。
也就是
P(CQ)=P(CQ)/(PCQ+P(CK)+P(CCO))
例题:
10个球,4白6红,每次取一个(不放回)
求第2次取红球的概率
已知第2次取红球,球第1次取白球的概率
定义A1:第1次取白球,A2:第1次取红球,B:第2次取红球
求:P(B)
求:P(A1|B)
求P(B)即全概率公式应用,这里就不加赘述了。
然后求P(A1|B)……贝叶斯定理,这里也不加赘述了。
然后我们来用贝叶斯公式来解决三扇门问题:
首先,我们设的不是是否能得到汽车概率,而是汽车在哪个门里的概率
(前提是有 123 1 2 3 123 3个门)
P ( 1 ) = P ( 2 ) = P ( 3 ) = 1 / 3 P(1)=P(2)=P(3)=1/3 P(1)=P(2)=P(3)=1/3
设打开的是2门,那么可得
P(汽车在1门|选择1门,打开2门)
P(汽车在2门|选择1门,打开2门)
P(汽车在3门|选择1门,打开2门)
由贝叶斯定理可得:
P ( 汽 车 在 1 门 ∣ 选 择 1 门 , 打 开 2 门 ) P(汽车在1门|选择1门,打开2门) P(汽车在1门∣选择1门,打开2门)= P ( 选 择 1 门 , 打 开 2 门 ∣ 汽 车 在 1 门 ) ∗ P ( 汽 车 在 1 门 ) P ( 选 择 1 门 , 打 开 2 门 ) \frac{P(选择1门,打开2门|汽车在1门)*P(汽车在1门)}{P(选择1门,打开2门)} P(选择1门,打开2门)P(选择1门,打开2门∣汽车在1门)∗P(汽车在1门)
P ( 汽 车 在 2 门 ∣ 选 择 1 门 , 打 开 2 门 ) P(汽车在2门|选择1门,打开2门) P(汽车在2门∣选择1门,打开2门)= P ( 选 择 1 门 , 打 开 2 门 ∣ 汽 车 在 2 门 ) ∗ P ( 汽 车 在 2 门 ) P ( 选 择 1 门 , 打 开 2 门 ) \frac{P(选择1门,打开2门|汽车在2门)*P(汽车在2门)}{P(选择1门,打开2门)} P(选择1门,打开2门)P(选择1门,打开2门∣汽车在2门)∗P(汽车在2门)
P ( 汽 车 在 3 门 ∣ 选 择 1 门 , 打 开 2 门 ) P(汽车在3门|选择1门,打开2门) P(汽车在3门∣选择1门,打开2门)= P ( 选 择 1 门 , 打 开 2 门 ∣ 汽 车 在 3 门 ) ∗ P ( 汽 车 在 3 门 ) P ( 选 择 1 门 , 打 开 2 门 ) \frac{P(选择1门,打开2门|汽车在3门)*P(汽车在3门)}{P(选择1门,打开2门)} P(选择1门,打开2门)P(选择1门,打开2门∣汽车在3门)∗P(汽车在3门)
由此只需求出这些基本事件的答案:
因为如果汽车在1门,且选手选对了,那么主持人要么打开2门要么打开3门,即 1 2 \frac{1}{2} 21
P ( 最 初 选 择 1 门 , 主 持 人 打 开 2 门 ∣ 汽 车 在 1 门 ) P(最初选择1门,主持人打开2门|汽车在1门) P(最初选择1门,主持人打开2门∣汽车在1门)= 1 2 \frac{1}{2} 21
……如果车在2门,主持人不可能打开2门
P ( 最 初 选 择 1 门 , 主 持 人 打 开 2 门 ∣ 汽 车 在 2 门 ) P(最初选择1门,主持人打开2门|汽车在2门) P(最初选择1门,主持人打开2门∣汽车在2门)= 0 0 0
车在3门,主持人只能打开2门,所以是1
P ( 最 初 选 择 1 门 , 主 持 人 打 开 2 门 ∣ 汽 车 在 3 门 ) P(最初选择1门,主持人打开2门|汽车在3门) P(最初选择1门,主持人打开2门∣汽车在3门)= 1 1 1
P ( 最 初 选 择 1 门 , 主 持 人 打 开 2 门 ) P(最初选择1门,主持人打开2门) P(最初选择1门,主持人打开2门) 这个怎么求呢,很玄,看图。
事件发生概率 选门1,开门2的概率
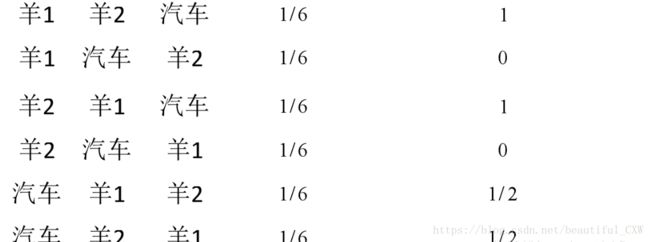
可得概率是 1 2 \frac{1}{2} 21
所以可以得到答案:
P ( 汽 车 在 1 门 ∣ 选 择 1 门 , 打 开 2 门 ) = 1 3 P(汽车在1门|选择1门,打开2门)=\frac{1}{3} P(汽车在1门∣选择1门,打开2门)=31
P ( 汽 车 在 2 门 ∣ 选 择 1 门 , 打 开 2 门 ) = 0 P(汽车在2门|选择1门,打开2门)=0 P(汽车在2门∣选择1门,打开2门)=0
P ( 汽 车 在 3 门 ∣ 选 择 1 门 , 打 开 2 门 ) = 2 3 P(汽车在3门|选择1门,打开2门)=\frac{2}{3} P(汽车在3门∣选择1门,打开2门)=32
也就是说,不换, 1 3 \frac{1}{3} 31,换了, 2 3 \frac{2}{3} 32
到此为止。
这大概是概率基本入门了吧……恕鄙人水平有限。
浅谈数学期望
可能比起概率来,我数学期望的水平更差了吧…………
数学期望(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量的加权平均值的大小。此处加权即指该随机变量对应的概率。
设随机变量X的取值为X1,X2,……,Xn,
P(X1),P(X2),…,P(Xn) 为X对应取值的概率,
则:E(X)=X1 P(X1) + X2 P(X2)+…+ Xn P(Xn) =ΣXkP(Xk)
举个例子:
假设我们来玩一个游戏,一共52张牌,其中有4个A。我们一元钱赌一把,如果你抽中了A,那么我给你10元钱,否则你的一元钱就输给我了,求你赢钱的数学期望。
抽中A:概率4/52=1/13
抽不中:概率12/13
期望: 1 / 13 ∗ 10 + 12 / 13 ∗ ( − 1 ) = − 2 / 13 1/13 * 10 + 12/13*(-1)=-2/13 1/13∗10+12/13∗(−1)=−2/13
这个例子哪里都有……,我对于数学期望的理解也就………………
啊,加油,共勉。