Grid Coloring（构造）

Grid Coloring

题目描述

Roundgod draws a grid graph of size $n$ with $n\times n$ cells. She can use one of $k$ colors to color every edge once, but lzr gives her some limits.

1. lzr loves balance. All colors should appear in the same number of times.
2. lzr loves complexity. The graph should not contain any monochromatic cycle.
3. lzr hates monotone. Each whole horizontal or vertical line of the graph should contain at least two colors.
   

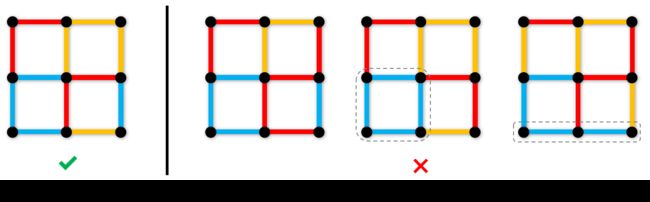
Roundgod is so divine that she doesn’t want to waste her god’s power to solve this problem. Could you give her a solution?

输入描述:

The input contains multiple test cases. The first line of input contains one integer $T(1\le T\le 100)$.
In the following $T$ lines, each line contains two integers $n,k(1\le n\le 200,1\le k\le 2(n+1)n)$ describing one test case.

输出描述:

For each test case, if there’s no solution, please output “-1”.
Otherwise, output $2(n+1)$ lines.
For the first $n+1$ lines, each line contains $n$ integers, denoting colors of edges on every horizontal line.
For the last $n+1$ lines, each line contain $n$ integers, denoting colors of edges on every vertical line.

输入

2
2 3
2 5

输出

1 2
3 1
3 2
1 3
2 1
2 3
-1

题解

S形构造，先横（每行 n 个）再竖（每行 n + 1 个），注意特判 n1 和 k1 的情况。

#include 
#include 
#include 
#include 
#include 
#include 
 
using namespace std;
#define ll long long
int row[410][410];
int col[410][410];
int t, n, k;
 
void judge() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cout << " " << row[i][j];
        }
        printf("\n");
        for (int j = 1; j <= (n + 1); j++) {
            cout << col[j][i] << " ";
        }
        printf("\n");
    }
    for (int j = 1; j <= n; j++) {
        cout << " " << row[n + 1][j];
    }
    printf("\n\n");
}
 
int main() {
    cin >> t;
    while (t--) {
        scanf("%d%d", &n, &k);
        if (2 * n * (n + 1) % k != 0 || k == 1 || n == 1) {
            printf("-1\n");
            continue;
        }
        int use = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                row[i][j] = use++;
                if (use > k) {
                    use = 1;
                }
            }
            for (int j = (n + 1); j >= 1; j--) {
                col[j][i] = use++;
                if (use > k) {
                    use = 1;
                }
            }
        }
        for (int j = 1; j <= n; j++) {
            row[n + 1][j] = use++;
            if (use > k) {
                use = 1;
            }
        }
 
//        judge();
 
        // print
        for (int i = 1; i <= (n + 1); i++) {
            for (int j = 1; j <= n; j++) {
                if (j == 1) {
                    printf("%d", row[i][j]);
                } else {
                    printf(" %d", row[i][j]);
                }
            }
            printf("\n");
        }
        for (int i = 1; i <= (n + 1); i++) {
            for (int j = 1; j <= n; j++) {
                if (j == 1) {
                    printf("%d", col[i][j]);
                } else {
                    printf(" %d", col[i][j]);
                }
            }
            printf("\n");
        }
 
    }
    return 0;
}