数据结构与算法(Python)——常见数据结构Part3(队列和循环队列)
写在前面
在上一节part2我们熟悉了栈结构,本节继续对其他常见数据结构进行总结。我们的目的是快速了解他们,对于它们涉及到的复杂的数据结构和算法,在这里并不全部展开,留在后期详述。
1. 队列
1.1 一般队列
同上一节栈类似,队列(Queue)结构也是插入和删除元素受到限制的线性结构。队列一般是一种只允许在线性结构的一端进行插入,另一端进行删除的结构,允许插入的一端称之为队尾(rear),允许删除的一端称之为对头(front)。这样的限制使得队列有一个重要特性:即先进入的元素先出,后进入的元素后出,这称之为后进后出(Last In Last Out,LILO),和栈的后进先出(LIFO)刚好相反。
队列和我们日常生活中看到的排队情况比较相似,如下图在单行道上的行车形成了一个队列(图片来自Data Structure and Algorithms - Queue):
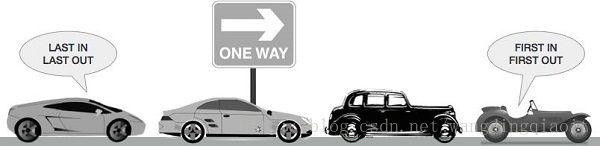
在单行道上,先开入的车辆先离开,后开入的车辆后离开,这就是我们队列的一个重要特性。
另外,如果允许在线性结构的两端都进行插入和删除操作,这种结构,我们称之为双端队列(Dequeue)。双端队列的应用远没有一般队列结构广泛。
在计算中的队列结构看起来是这样的(图片来自Data Structure and Algorithms - Queue):
队列结构既可以使用数组,也可以使用链表来实现。
1.2 队列的实现
在Python中没有显式提供队列,不过使用list结构来模拟一个队列:
queue = ['a']
queue.append('b') # 入队操作
queue.append('c')
print(queue) # ['a', 'b', 'c']
content = queue.pop(0) # 出队操作
print(content) # 'a'
print(queue) # ['b', 'c']另外Collections模块还提供了双端队列模块供使用:
import collections
queue = collections.deque()
queue.append('a')
queue.append('b')
queue.append('c')
print(queue.popleft()) # 'a'
print(queue) # deque(['b', 'c'])
queue.clear()
print(queue) # deque([]) 下面我们利用list构成数组的特点,来手动实现一个queue结构:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
class Queue(object):
"""
大小固定的队列 存在空间浪费
"""
MAX_QUEUE_SIZE = 4
def __init__(self):
self.data = [None for _ in range(Queue.MAX_QUEUE_SIZE)] # 模拟固定大小数组
self.front, self.rear = 0, 0
def enter_queue(self, x):
if self.is_full():
raise Exception("queue is full.")
self.data[self.rear] = x
self.rear += 1
return True
def del_queue(self):
if self.front == self.rear:
return None
val = self.data[self.front]
self.front += 1
return val
def is_empty(self):
return self.front == self.rear
def is_full(self):
return self.rear >= Queue.MAX_QUEUE_SIZE
def size(self):
return self.rear - self.front
def get_front(self):
if not self.is_empty():
return self.data[self.front]
else:
return None
def clear(self):
self.__init__()
def __str__(self):
ret_str = "queue["
for x in range(self.front, self.rear):
ret_str += self.data[x] + ", "
ret_str += "]"
return ret_str
def __repr__(self):
return self.__str__()为上述队列类编写测试用例:
if __name__ == "__main__":
my_queue = Queue()
my_queue.enter_queue('a')
my_queue.enter_queue('b')
my_queue.enter_queue('c')
my_queue.enter_queue('d')
print('front is: ', my_queue.get_front(), my_queue)
print('delete head:', my_queue.del_queue())
print("is full ? ", my_queue.is_full(), my_queue)
print('element size: ', my_queue.size())
my_queue.clear()
print("after clear, is empty ? ", my_queue.is_empty(), my_queue)运行测试用例输出得到:
('front is: ', 'a', queue[a, b, c, d, ])
('delete head:', 'a')
('is full ? ', True, queue[b, c, d, ])
('element size: ', 3)
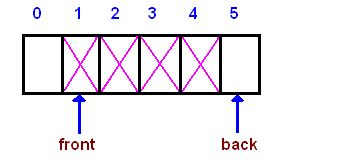
('after clear, is empty ? ', True, queue[])上面的队列实现中队头指针front始终指向队头元素,尾指针rear始终指向队尾元素的下一个位置。 初始化时队列为空,front = rear;加满元素时,队列满了,此时rear = Queue.MAX_QUEUE_SIZE。 存在一个问题,当队列中元素装满,然后出队后,队列实际未满,但是却无法加入新的元素,如下图所示(图片来自Stacks and Queues):
我们看到上面的图中(图中back指针即我们这里的rear指针),还有两个0和1索引的位置没有填满,但是此时队列已经无法加入其它元素了。
解决这个问题的方法,一种是使用链表实现队列,在链表中根据需要动态的添加和删除元素,这个练习留给读者去完成;另一种方法是使用一个小的技巧,将上面数组中未被占用的位置循环利用,这种循环利用队列中位置的方法构造了一个新的队列,我们称之为循环队列(Circular queue)。
1.2 循环队列
1.2.1 循环队列特点
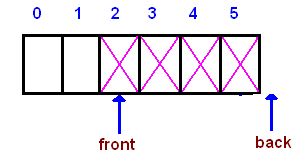
继续上面的话题,如果我们在队列满时,允许尾指针回过头来继续指向那些尚未被使用的空间,则既能维持队列先入先出的特性,又提供了空间的利用率。队尾指针重新指向未被利用的空间,如下图所示:
按照之前我们实现的Queue类计算方法,当在位置5插入元素后,我们更新尾指针rear将执行: self.rear += 1这样rear指针指向了队列尾部下一位置6,这个位置已经超出了图示的队列长度,显然无法继续加入元素了;但是对于循环队列,我们要想让rear指针指向下一个可利用的位置0,那么该如何计算呢?
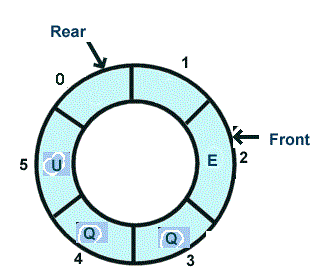
循环队列实际上是对一维连续数组在形象上进行了一次转换,将其转换为一个环状结构,虽然物理上的存储仍然是一维连续的,如下图所示为循环队列环状形象:
上面的队列长度为6,当前插入元素5后,如果要让尾指针指向0,而不是之前计算的6,将用到求模运算符: self.rear = (self.rear + 1) % 6 这样得到self.rear = 0,从而开始了指针的循环,利用上了未被占用的空间。
1.2.2 循环队列的实现
结合上面的分析,我们自己动手实现一个循环队列:
class CircularQueue(object):
"""
循环队列
"""
MAX_QUEUE_SIZE = 6
def __init__(self):
self.data = [None for _ in range(CircularQueue.MAX_QUEUE_SIZE)] # 模拟固定大小数组
self.front, self.rear = 0, 0
def enter_queue(self, x):
if self.is_full():
raise Exception("queue is full.")
self.data[self.rear] = x
self.rear = (self.rear + 1) % CircularQueue.MAX_QUEUE_SIZE
return True
def del_queue(self):
if self.is_empty():
return None
val = self.data[self.front]
self.front = (self.front + 1) % CircularQueue.MAX_QUEUE_SIZE
return val
def is_empty(self):
return self.front == self.rear
def is_full(self):
return (self.rear + 1) % CircularQueue.MAX_QUEUE_SIZE == self.front # 牺牲一个单元 用来区分满 还是空
def size(self):
return (self.rear - self.front + CircularQueue.MAX_QUEUE_SIZE) % CircularQueue.MAX_QUEUE_SIZE
def get_front(self):
if not self.is_empty():
return self.data[self.front]
else:
return None
def clear(self):
self.__init__()
def __str__(self):
ret_str = "queue["
start, end = self.front, self.rear
while start != end:
ret_str += str(self.data[start]) + ", "
start = (start + 1) % CircularQueue.MAX_QUEUE_SIZE
ret_str += "]"
return ret_str
def __repr__(self):
return self.__str__()在上述实现中需要说明几点:
循环队列中使用了指向队头的front和指向队尾的rear指针,rear指针总是指向队尾元素的下一位置。
当队列空时,
front = rear;当队列满时我们牺牲了一个单元,使用(self.rear + 1) % CircularQueue.MAX_QUEUE_SIZE = self.front来表示队列满的状态。另外的方法,例如保存一个变量要么它表示队列是否满,要么保存队列中元素个数用来区分是否队列满。通过求模运算符,实现了front和rear指针以“圆形的形式“遍历队列,对于释放的队头元素占用的空间,又能重复利用起来。
为上述循环队列类编写测试用例如下:
if __name__ == "__main__":
my_queue = CircularQueue()
my_queue.enter_queue('a')
my_queue.enter_queue('b')
my_queue.enter_queue('c')
my_queue.enter_queue('d')
my_queue.enter_queue('e')
print('is full ?', my_queue.is_full(), my_queue)
print('front pos: ', my_queue.front, ' rear pos:', my_queue.rear)
print('front is: ', my_queue.get_front(), my_queue)
print('delete head:', my_queue.del_queue(), my_queue)
print("enter 'f'")
my_queue.enter_queue('f')
print('element size: ', my_queue.size(), my_queue)
print('front pos: ', my_queue.front, ' rear pos:', my_queue.rear)
my_queue.clear()
print("after clear ,is empty ? ", my_queue.is_empty(), my_queue)程序输出:
('is full ?', True, queue[a, b, c, d, e, ])
('front pos: ', 0, ' rear pos:', 5)
('front is: ', 'a', queue[a, b, c, d, e, ])
('delete head:', 'a', queue[b, c, d, e, ])
enter 'f'
('element size: ', 5, queue[b, c, d, e, f, ])
('front pos: ', 1, ' rear pos:', 0)
('after clear ,is empty ? ', True, queue[])1.3 队列应用
队列和栈一样是一种限制性插入和移除的线性结构,队列的这种先入先出特性,适合于需要顺序处理集合中元素的情形,例如先来先服务的操作系统作业队列。本节讨论的一般队列和循环队列,实际上还有一种高级的数据结构优先级队列(priority queue),能够以某种优先级形式出队,这个结构将在后面学习了树的数据结构后学习。
最后来看一个用双端队列判定一个字符串是否回文的解决方案。回文,是一种正着念和反着念一样的字符串(空字符串和长度为1的字符串算作回文),这里排除字符串中标点符号,不区分大小写,则算法实现为:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import collections
def is_palindrome_str(s):
"""
:type s: str
:rtype: bool
"""
de_queue = collections.deque([x.lower() for x in s if x.isdigit() or x.isalpha() ])
while len(de_queue) >= 2:
head, tail = de_queue.popleft(), de_queue.pop()
if head != tail:
return False
return True
if __name__ == "__main__":
test_str = "A man, a plan, a canal: Panama"
print('input str= ', test_str, " is palindrome ? ", is_palindrome_str(test_str))
test_str = "race a car"
print('input str= ', test_str, " is palindrome ? ", is_palindrome_str(test_str))
test_str = "abcecba"
print('input str= ', test_str, " is palindrome ? ", is_palindrome_str(test_str))上述程序输出:
('input str= ', 'A man, a plan, a canal: Panama', ' is palindrome ? ', True)
('input str= ', 'race a car', ' is palindrome ? ', False)
('input str= ', 'abcecba', ' is palindrome ? ', True)感兴趣地可以去Leetcode在线OJ系统练习这个题目。
本节学习了队列这一数据结构,下节将开始学习灵活多变的树数据结构,再会。