Greeks介绍 ,python实现方案
Greeks介绍 ,python实现方案
##对冲的介绍
以期权举例能更容易的理解对冲的意义,持有期权有两种形式:
- naked position
- covered position
第一种顾名思义就是单独持有期权,假设一个人write a call option on a stock,如果到期日时股票价格高于行权价格,那么这个人就会遭受损失,股票价格越高这个损失越多,理论上资产价格可以无限增长但不能低于0,所以这个人的风险就是无限大的。
如果这个人同时持有同种股票,那么当股票价格上升时虽然option遭到损失,但是持有的股票确可以受益,在一定的stock和option的比例下,这个人可以实现0风险,拿到一个risk-free rate。这就是对冲的意义。
在金融市场中,不同的机构或这个人对于风险的需求不同,而作为一个完善的金融市场能提供多种的可能性也是其基本的职能。不同产品的诞生,包括不同的结构化,不同的风险构成,不同的期限结构,需要大量的金融工程的人士来进行设计,估值,架构。而对于如何对冲自己持有的金融产品的风险则是基金,资管,银行等机构中的人士需要重点关注的对象。
##Greeks介绍
Greeks包含多种指标,其主要用来帮助专业人士来进行对冲工作,通过不同的greeks exposure我们可以进行不同的金融产品的买卖来有效的稀释风险,达到整体的风险等级需要。
###Delta
Delta: option价格的变化随着underlying asset价格变化的比率
举个例子,假设一个人sell 1000 call option,我们可以计算出delta for this option 是0.6,那么如果我想对冲掉风险,我们就可以买入underlying asset(0.6✖️1000=600)。这样一个组合就是delta neutral的。
Delta 的计算方法有两种:
- Delta= change in call option price/ change in underlying asset price
- Delta= N(d1) 之前文章提到的BSM模型中的一部分
随便画了一个call option的delta 的图,可以看出随着underlying asset价格的变化delta是不断变化的,所以为了保持delta中性我们也需要随时调整参数。

###Theta
Theta:option价格的变化随着到期时间的变化的比率
Theta 的计算方法也分为两种,第一种就是change in price/change in time。
第二种也要用到BSM模型中的一部分具体的公式很复杂,可以网上搜索一下很快就出来了。
介绍下theta的特点吧:
- 对于put和call,theta的影响是一样的
- 当underlying asset的价格等于执行价格时候,theta是最明显的,也就是在at-the-money的情况下
###Gamma
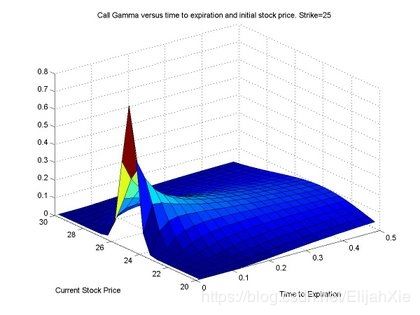
Gamma:delta的变化随着underlying asset价格变化的比率
公式同样,两种方法,一种是delta的导数,第二章运用BSM
Gamma,和delta同样的重要,delta仅仅能对冲掉价格小范围变化产生的风险,而gamma则能对冲掉价格大范围变化的风险。所以同时使用delta和gamma是非常有必要的。
Gamma也有很多特点,图片可以看出其在at-the-money时是最大的也就是说delta的变化最大。
###Vega
Vega:形容的是option价格的变化随着sensitivity变化的比率
###Rho
Rho:形容的是option价格的变化随着risk-free rate变化的比率
##最后附上python的code
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import math
from BSM.option import d1f,N,dN
#
#Functions for greeks
#
def BSM_delta (St,K,t,T,r,sigma):
d1=d1f(St,K,t,T,r,sigma)
delta=N(d1)
return delta
def BSM_gamma(St,K,t,T,r,sigma):
d1=d1f(St,K,t,T,r,sigma)
gamma=dN(d1)/(St*sigma*math.sqrt(T-t))
return gamma
def BSM_theta(St,K,t,T,r,sigma):
d1 = d1f(St, K, t, T, r, sigma)
d2 = d1 - sigma * math.sqrt(T - t)
theta = -(St * dN(d1) * sigma / (2 * math.sqrt(T - t))
+ r * K * math.exp(-r * (T - t)) * N(d2))
return theta
def BSM_rho(St,K,t,T,r,sigma):
d1 = d1f(St, K, t, T, r, sigma)
d2 = d1 - sigma * math.sqrt(T - t)
rho = K * (T - t) * math.exp(-r * (T - t)) * N(d2)
return rho
def BSM_vega(St,K,t,T,r,sigma):
d1 = d1f(St, K, t, T, r, sigma)
vega = St * dN(d1) * math.sqrt(T - t)
return vega
#
#Plotting
#
def plot_greeks(function,greek):
# model parameters
St = 100.0 # index level
K = 100.0 # option strike
t = 0.0 # valuation date
T = 1.0 # maturity date
r = 0.05 # risk-less short rate
sigma = 0.2 # volatility
# Greek Calculations
tlist = np.linspace(0.01, 1, 50)
klist = np.linspace(80, 120, 50)
V = np.zeros((len(tlist), len(klist)), dtype=np.float)
for j in range(len(klist)):
for i in range(len(tlist)):
V[i, j] = function(St, klist[j], t, tlist[i], r, sigma)
# 3D Plotting
x, y = np.meshgrid(klist, tlist)
fig = plt.figure(figsize=(9, 5))
plot = Axes3D(fig)
plot.plot_wireframe(x, y, V)
plot.set_xlabel('strike $K$')
plot.set_ylabel('maturity $T$')
plot.set_zlabel('%s(K, T)' % greek)