梅森公式的形式和应用
梅森公式的推导(篇二):梅森公式的形式和应用
写在前:
本篇是《梅森公式的推导》的篇二,基础知识部分。介绍了梅森公式的形式和应用。篇一认识信号流图介绍了信号流图的基本概念和简单形式,篇三梅森公式的推导和探究尝试了梅森公式的推导和相关探究。
梅森公式,或称梅森增益公式,是在控制理论、自动化领域用于求取系统传递函数的公式。应用梅森公式将大大简化结构变换的计算。公式如下: T = ∑ i = 1 n T i Δ i Δ T=\frac{\sum_{i=1}^n T_i\Delta_i}{\Delta} T=Δ∑i=1nTiΔi
Δ \Delta Δ:系统的特征式
Δ = 1 − ∑ j L j + ∑ m , n L m L n − ∑ p , q , r L p L q L r + ⋯ \Delta=1-\sum\limits_{j} {L_j}+\sum\limits_{m,n} {L_mL_n}-\sum\limits_{p,q,r} {L_pL_qL_r}+\cdots Δ=1−j∑Lj+m,n∑LmLn−p,q,r∑LpLqLr+⋯
∑ j L j \sum\limits_{j} {L_j} j∑Lj是所有不同回路的增益之和; ∑ m , n L m L n \sum\limits_{m,n} {L_mL_n} m,n∑LmLn是所有两两不接触回路的增益乘积之和; ∑ p , q , r L p L q L r \sum\limits_{p,q,r} {L_pL_qL_r} p,q,r∑LpLqLr是所有三三不接触回路的增益乘积之和:…
n n n:前向通路总数
i i i:源节点和肼节点之间的第 i i i条前向通路的标号,显然 1 ≤ i ≤ n 1\le i\le n 1≤i≤n
T i T_i Ti:源节点和肼节点之间的第 i i i条前向通路的增益
Δ i \Delta_i Δi:将与第 i i i条前向通路相接触的回路的增益除去后所余下的部分,称为余因子式;相当于在系统特征式 Δ \Delta Δ内部去掉相关项
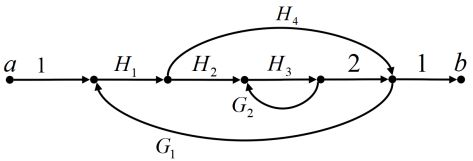
(1)首先找出所有回路:
L 1 = G 2 H 3 L_1=G_2H_3 L1=G2H3
L 2 = 2 G 1 H 1 H 2 H 3 L_2=2G_1H_1H_2H_3 L2=2G1H1H2H3
L 3 = G 1 H 1 H 4 L_3=G_1H_1H_4 L3=G1H1H4
(2)求特征行列式:
T 1 = 2 H 1 H 2 H 3 T_1=2H_1H_2H_3 T1=2H1H2H3
T 2 = H 1 H 4 T_2=H_1H_4 T2=H1H4
(4)求各前向通路的余因子式:
Δ 1 = 1 \Delta_1=1 Δ1=1
Δ 2 = 1 − L 1 = 1 − G 2 H 3 \Delta_2=1-L_1=1-G_2H_3 Δ2=1−L1=1−G2H3
(5)根据梅森公式得系统的增益(源点到肼点):
T = ∑ i = 1 n T i Δ i Δ = T 1 Δ 1 + T 2 Δ 2 Δ = 2 H 1 H 2 H 3 + H 1 H 4 ⋅ ( 1 − G 2 H 3 ) 1 − ( G 2 H 3 + 2 G 1 H 1 H 2 H 3 + G 1 H 1 H 4 ) + G 1 G 2 H 1 H 3 H 4 T=\frac{\sum_{i=1}^n T_i\Delta_i}{\Delta}=\frac{T_1\Delta_1+T_2\Delta_2}{\Delta}=\frac{2H_1H_2H_3+H_1H_4\cdot(1-G_2H_3)}{1-(G_2H_3+2G_1H_1H_2H_3+G_1H_1H_4)+G_1G_2H_1H_3H_4} T=Δ∑i=1nTiΔi=ΔT1Δ1+T2Δ2=1−(G2H3+2G1H1H2H3+G1H1H4)+G1G2H1H3H42H1H2H3+H1H4⋅(1−G2H3)
我感觉看文字版梅森公式的介绍和应用不如看视频讲解的接受的效率和质量高,推荐西电郭宝龙老师的《信号与系统》讲解,其中一节是梅森公式,B站上就有。
将在篇三梅森公式的推导和探究尝试梅森公式的推导和相关探究。不需要或者不太想了解梅森公式的推导或者某些计算的意义的童鞋就可以止步啦,这个推导还挺繁琐的,不过过程还挺好玩的。