【数学】张宇概率论九讲笔记
文章目录
- 随机事件与概率
- 一维随机变量及分布
- 分布函数的性质
- 离散型随机变量的分布律与分布函数
- 连续型随机变量的性质
- 常见分布
- 期望方差
- 宇哥笔记
- 随机事件与概率
- 古典概型
- 定义
- 随机分配(占位)
- 简单随机抽样
- 几何概型
- 重要公式
- 一维随机变量及其分布
- 随机变量与分布函数
- 离散型随机变量
- 连续型随机变量
- X~F(x)
- 八个常见分布
- 多元随机变量及其分布
- 概念
- 用分布求概率
- 数字特征
- 概念
- 数学期望与方差
- 协方差与相关系数
- 例题
- 大数定律与中心极限定理
- 依概率收敛
- 三个定律与两个定理
- 大数定律
- 中心极限定理
- 数理统计初步
- 总体与样本
- 点估计
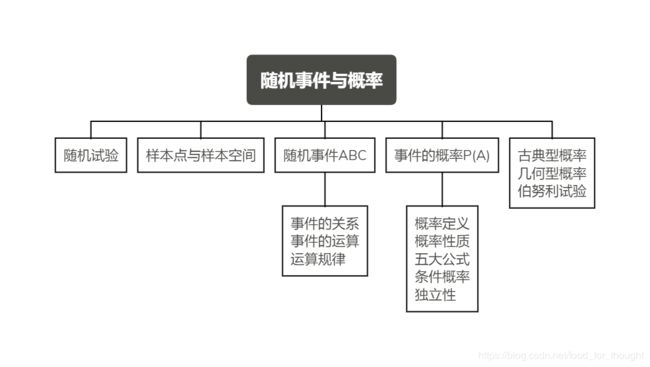
随机事件与概率
1. 排 列 组 合 排 列 A n r = n ( n − 1 ) ⋯ ( n − r + 1 ) 从 n 个 不 同 的 元 素 中 任 取 r 个 , 按 一 定 顺 序 排 成 一 列 组 合 C n r = n ! ( n − r ) ! r ! = A n r r ! 从 n 个 不 同 的 元 素 中 任 取 r 个 , 不 计 顺 序 排 成 一 组 2. 五 大 公 式 加 法 公 式 : P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) 减 法 公 式 : P ( A − B ) = P ( A ) − P ( A B ) 乘 法 公 式 : P ( A B ) + P ( A ) P ( B ∣ A ) 全 概 率 公 式 : P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) 逆 概 率 公 式 : P ( A j ∣ B ) = P ( A j B ) P ( B ) = P ( A j ) P ( B ∣ A j ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) 3. 条 件 概 率 P ( B ∣ A ) = P ( A B ) P ( A ) ⟹ P ( A B ) = P ( A ) ⋅ P ( B ∣ A ) 4. 独 立 P ( A B ) = P ( A ) P ( B ) 5. 伯 努 利 试 验 P ( X = k ) = C N K p k ( 1 − p ) n − k \begin{aligned} 1.&\color{red}{排列组合}\\ &排列A_n^r=n(n-1)\cdots(n-r+1)\\ &从n个不同的元素中任取r个,按一定顺序排成一列\\ &组合C_n^r=\frac{n!}{(n-r)!r!}=\frac{A_n^r}{r!}\\ &从n个不同的元素中任取r个,不计顺序排成一组\\ 2.&\color{red}{五大公式}\\ &加法公式:P(A\cup B)=P(A)+P(B)-P(AB)\\ &减法公式:P(A-B)=P(A)-P(AB)\\ &乘法公式:P(AB)+P(A)P(B|A)\\ &全概率公式:P(A)=\sum_{i=1}^nP(B_i)P(A|B_i)\\ &逆概率公式:P(A_j|B)=\frac{P(A_jB)}{P(B)}=\frac{P(A_j)P(B|A_j)}{\sum_{i=1}^nP(A_i)P(B|A_i)}\\ 3.&\color{red}{条件概率}\\ &P(B|A)=\frac{P(AB)}{P(A)}\implies P(AB)=P(A)\cdot P(B|A)\\ 4.&\color{red}{独立}\\ &P(AB)=P(A)P(B)\\ 5.&\color{red}{伯努利试验}\\ &P(X=k)=C_N^Kp^k(1-p)^{n-k}\\ \end{aligned} 1.2.3.4.5.排列组合排列Anr=n(n−1)⋯(n−r+1)从n个不同的元素中任取r个,按一定顺序排成一列组合Cnr=(n−r)!r!n!=r!Anr从n个不同的元素中任取r个,不计顺序排成一组五大公式加法公式:P(A∪B)=P(A)+P(B)−P(AB)减法公式:P(A−B)=P(A)−P(AB)乘法公式:P(AB)+P(A)P(B∣A)全概率公式:P(A)=i=1∑nP(Bi)P(A∣Bi)逆概率公式:P(Aj∣B)=P(B)P(AjB)=∑i=1nP(Ai)P(B∣Ai)P(Aj)P(B∣Aj)条件概率P(B∣A)=P(A)P(AB)⟹P(AB)=P(A)⋅P(B∣A)独立P(AB)=P(A)P(B)伯努利试验P(X=k)=CNKpk(1−p)n−k
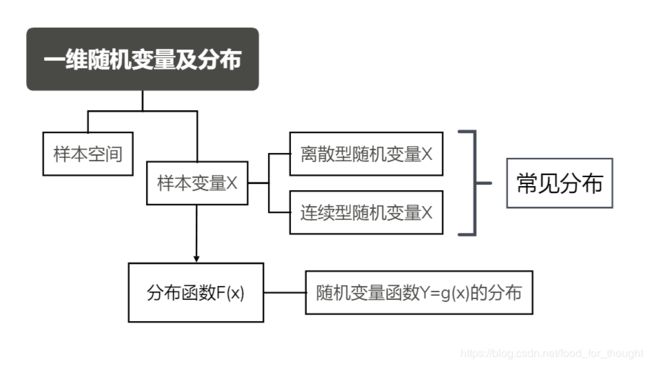
一维随机变量及分布
分布函数的性质
1. lim x → − ∞ F ( x ) = 0 , 记 为 F ( − ∞ ) = 0 , lim x → + ∞ F ( x ) = 1 , 记 为 F ( + ∞ ) = 1 2. F ( x ) 是 单 调 非 减 函 数 3. F ( x ) 是 右 连 续 函 数 , F ( x + 0 ) = F ( x ) 若 x ∈ D 为 一 随 机 事 件 , 则 其 概 率 为 P ( x ∈ D ) = ∫ D f ( x ) d x \begin{aligned} &1.\lim_{x\to-\infty}F(x)=0,记为F(-\infty)=0,\lim_{x\to+\infty}F(x)=1,记为F(+\infty)=1\\ &2.F(x)是单调非减函数\\ &3.F(x)是右连续函数,F(x+0)=F(x)\\ &若x\in D为一随机事件,则其概率为P(x\in D)=\int_Df(x)dx\\ \end{aligned} 1.x→−∞limF(x)=0,记为F(−∞)=0,x→+∞limF(x)=1,记为F(+∞)=12.F(x)是单调非减函数3.F(x)是右连续函数,F(x+0)=F(x)若x∈D为一随机事件,则其概率为P(x∈D)=∫Df(x)dx
离散型随机变量的分布律与分布函数
x 1 2 3 P 0.1 0.5 0.4 F ( x ) = { 0 , x < 1 0.1 , 1 ≤ x < 2 0.6 , 2 ≤ x < 3 1 , 3 ≤ x \begin{aligned} & \begin{array}{c|c|c|c} x & 1 & 2 & 3 \\ \hline P & 0.1 & 0.5 & 0.4 \end{array}\\ &F(x)=\begin{cases}0,x<1\\0.1,1\leq x<2\\0.6,2\leq x<3\\1,3\leq x\end{cases} \end{aligned} xP10.120.530.4F(x)=⎩⎪⎪⎪⎨⎪⎪⎪⎧0,x<10.1,1≤x<20.6,2≤x<31,3≤x
连续型随机变量的性质
1. f ( x ) ≥ 0 2. ∫ − ∞ + ∞ f ( x ) d x = 1 3. 对 于 ∀ x 1 < x 2 , P ( x 1 < x ≤ x 2 ) = ∫ x 1 x 2 f ( t ) d t 4. f ( x ) 在 连 续 点 处 可 导 , 即 F ′ ( x ) = f ( x ) 常 考 的 两 个 积 分 { ∫ 0 + ∞ x n e − x d x = n ! ∫ − ∞ + ∞ e − x 2 d x = π \begin{aligned} &1.f(x)\geq0\\ &2.\int_{-\infty}^{+\infty}f(x)dx=1\\ &3.对于\forall x_1< x_2,P(x_1< x\leq x_2)=\int_{x_1}^{x_2}f(t)dt\\ &4.f(x)在连续点处可导,即F'(x)=f(x)\\ &常考的两个积分\begin{cases}\int_0^{+\infty}x^ne^{-x}dx=n!\\\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt\pi\end{cases} \end{aligned} 1.f(x)≥02.∫−∞+∞f(x)dx=13.对于∀x1<x2,P(x1<x≤x2)=∫x1x2f(t)dt4.f(x)在连续点处可导,即F′(x)=f(x)常考的两个积分{∫0+∞xne−xdx=n!∫−∞+∞e−x2dx=π
常见分布
离 散 型 定 义 0 与 1 P ( X = k ) = C n k p k ( 1 − p ) n − k P ( X = k ) = λ k e − λ k ! 称 呼 0 − 1 分 布 二 项 分 布 泊 松 分 布 记 号 X ∼ B ( 1 , p ) X ∼ B ( n , p ) X ∼ P ( λ ) 参 数 p p λ 背 景 一 次 伯 努 利 试 验 成 功 或 失 败 的 次 数 n 次 伯 努 利 试 验 成 功 k 次 , 失 败 n − k 次 例 如 每 天 收 到 电 话 、 短 信 的 次 数 E X p n p λ D X p ( 1 − p ) n p ( 1 − p ) λ 连 续 型 定 义 f ( x ) = { 1 b − a , a ≤ x ≤ b 0 , 其 他 f ( x ) = { λ e − λ x , x > 0 0 , x ≤ 0 ( λ > 0 ) f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 称 呼 均 匀 分 布 指 数 分 布 正 态 分 布 记 号 X ∼ U [ a , b ] X ∼ E ( λ ) X ∼ N ( μ , σ 2 ) 参 数 a , b λ μ , σ 背 景 等 公 交 、 地 铁 、 电 梯 反 映 使 用 寿 命 、 生 命 特 征 的 现 象 考 试 成 绩 的 分 布 E X a + b 2 1 λ μ D X ( b − a ) 2 12 1 σ 2 σ 2 特 殊 P ( x > t ) = e − λ t ( t > 0 ) X ∼ N ( 0 , 1 ) → φ ( x ) = 1 2 π e − x 2 2 \begin{aligned} &\color{red}{离散型}\\ & \begin{array}{c|c|c|c} 定义 & 0与1 & P(X=k)=C_n^kp^k(1-p)^{n-k} & P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!} \\ \hline 称呼 & 0-1分布 & 二项分布 & 泊松分布 \\\hline 记号 & X\sim B(1,p) & X\sim B(n,p) & X\sim P(\lambda) \\\hline 参数 & p & p & \lambda\\\hline 背景 & 一次伯努利试验成功或失败的次数 & n次伯努利试验成功k次,失败n-k次 & 例如每天收到电话、短信的次数\\\hline EX & p & np & \lambda \\\hline DX & p(1-p) & np(1-p) & \lambda \\ \end{array}\\ &\color{red}{连续型}\\ & \begin{array}{c|c|c|c} 定义 & f(x)=\begin{cases}\frac1{b-a},a\leq x\leq b\\0,其他\end{cases} & f(x)=\begin{cases}\lambda e^{-\lambda x},x>0\\0,x\leq 0\end{cases}(\lambda>0) & f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \\ \hline 称呼 & 均匀分布 & 指数分布 & 正态分布 \\\hline 记号 & X\sim U[a,b] & X\sim E(\lambda) & X\sim N(\mu,\sigma^2) \\\hline 参数 & a,b & \lambda & \mu,\sigma\\\hline 背景 & 等公交、地铁、电梯 & 反映使用寿命、生命特征的现象 & 考试成绩的分布\\\hline EX & \frac{a+b}2 & \frac1\lambda & \mu \\\hline DX & \frac{(b-a)^2}{12} & \frac1{\sigma^2} & \sigma^2 \\\hline 特殊 & & P(x>t)=e^{-\lambda t}(t>0) & X\sim N(0,1)\to\varphi(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}2} \end{array} \end{aligned} 离散型定义称呼记号参数背景EXDX0与10−1分布X∼B(1,p)p一次伯努利试验成功或失败的次数pp(1−p)P(X=k)=Cnkpk(1−p)n−k二项分布X∼B(n,p)pn次伯努利试验成功k次,失败n−k次npnp(1−p)P(X=k)=k!λke−λ泊松分布X∼P(λ)λ例如每天收到电话、短信的次数λλ连续型定义称呼记号参数背景EXDX特殊f(x)={b−a1,a≤x≤b0,其他均匀分布X∼U[a,b]a,b等公交、地铁、电梯2a+b12(b−a)2f(x)={λe−λx,x>00,x≤0(λ>0)指数分布X∼E(λ)λ反映使用寿命、生命特征的现象λ1σ21P(x>t)=e−λt(t>0)f(x)=2πσ1e−2σ2(x−μ)2正态分布X∼N(μ,σ2)μ,σ考试成绩的分布μσ2X∼N(0,1)→φ(x)=2π1e−2x2
期望方差
期 望 : E ( x ) = ∫ − ∞ + ∞ x d [ F ( x ) ] = { ∑ i x i p i , X 为 离 散 型 随 机 变 量 ∫ − ∞ ∞ x f ( x ) d x , X 为 连 续 型 随 机 变 量 若 随 机 变 量 X 的 概 率 分 布 已 知 , 则 随 机 变 量 函 数 g ( x ) 的 数 学 期 望 为 E ( g ( X ) ) = { ∑ i g ( x i ) p i , X 为 离 散 型 ∫ − ∞ ∞ g ( x ) f ( x ) d x , X 为 连 续 型 性 质 : E ( c ) = C E ( c X ) = C E ( X ) E ( X + Y ) = E ( X ) + E ( Y ) E ( X Y ) = E ( X ) E ( Y ) 方 差 : D ( X ) = E [ X − E ( X ) ] 2 = { ∑ i [ x i − E ( X ) ] 2 p i , 当 X 为 离 散 型 时 ∫ − ∞ + ∞ [ x − E ( X ) ] 2 f ( x ) d x , 当 X 为 连 续 型 时 性 质 : D ( c ) = 0 D ( c X ) = C 2 D ( X ) D ( X + Y ) = D ( X ) + D ( Y ) − 2 E { [ X − E ( X ) ] [ Y − E ( Y ) ] } D ( X ) = e ( X 2 ) − [ E ( X ) ] 2 D ( X + Y ) = D ( X ) + D ( Y ) ( 独 立 ) \begin{aligned} 期望:&E(x)=\int_{-\infty}^{+\infty}xd[F(x)]=\begin{cases}\sum_ix_ip_i,X为离散型随机变量\\\int_{-\infty}^{\infty}xf(x)dx,X为连续型随机变量\end{cases}\\ &若随机变量X的概率分布已知,则随机变量函数g(x)的数学期望为E(g(X))=\begin{cases}\sum_ig(x_i)p_i,X为离散型\\\int_{-\infty}^{\infty}g(x)f(x)dx,X为连续型\end{cases}\\ 性质:&E(c)=C\quad E(cX)=CE(X)\quad E(X+Y)=E(X)+E(Y)\quad E(XY)=E(X)E(Y)\\ 方差:&D(X)=E[X-E(X)]^2=\begin{cases}\sum_i[x_i-E(X)]^2p_i,当X为离散型时\\\int_{-\infty}^{+\infty}[x-E(X)]^2f(x)dx,当X为连续型时\end{cases}\\ 性质:&D(c)=0\quad D(cX)=C^2D(X)\\ &D(X+Y)=D(X)+D(Y)-2E\{[X-E(X)][Y-E(Y)]\}\\ &D(X)=e(X^2)-[E(X)]^2\quad D(X+Y)=D(X)+D(Y)(独立) \end{aligned} 期望:性质:方差:性质:E(x)=∫−∞+∞xd[F(x)]={∑ixipi,X为离散型随机变量∫−∞∞xf(x)dx,X为连续型随机变量若随机变量X的概率分布已知,则随机变量函数g(x)的数学期望为E(g(X))={∑ig(xi)pi,X为离散型∫−∞∞g(x)f(x)dx,X为连续型E(c)=CE(cX)=CE(X)E(X+Y)=E(X)+E(Y)E(XY)=E(X)E(Y)D(X)=E[X−E(X)]2={∑i[xi−E(X)]2pi,当X为离散型时∫−∞+∞[x−E(X)]2f(x)dx,当X为连续型时D(c)=0D(cX)=C2D(X)D(X+Y)=D(X)+D(Y)−2E{[X−E(X)][Y−E(Y)]}D(X)=e(X2)−[E(X)]2D(X+Y)=D(X)+D(Y)(独立)
宇哥笔记
随机事件与概率
古典概型
定义
[ 定 义 ] 若 Ω 中 有 有 限 个 、 等 可 能 的 样 本 点 , 称 为 古 典 概 型 即 P ( A ) = A 中 样 本 点 个 数 Ω 中 样 本 点 数 [ 注 ] 1. 试 验 ( E ) 同 条 件 下 可 重 复 ; 试 验 结 果 不 止 一 个 ; 试 验 前 不 知 哪 个 结 果 会 出 现 2. Ω — — 样 本 空 间 — — 所 有 可 能 结 果 ; ω — — 样 本 点 [ 例 ] P ( 掷 出 奇 数 点 ) = 1 2 \begin{aligned} \ [定义]&若\Omega中有有限个、等可能的样本点,称为古典概型\\ &即P(A)=\frac{A中样本点个数}{\Omega中样本点数}\\ [注]&1.试验(E)同条件下可重复;试验结果不止一个;试验前不知哪个结果会出现\\ &2.\Omega——样本空间——所有可能结果;\omega——样本点\\ [例]&P(掷出奇数点)=\frac12\\ \end{aligned} [定义][注][例]若Ω中有有限个、等可能的样本点,称为古典概型即P(A)=Ω中样本点数A中样本点个数1.试验(E)同条件下可重复;试验结果不止一个;试验前不知哪个结果会出现2.Ω——样本空间——所有可能结果;ω——样本点P(掷出奇数点)=21
随机分配(占位)
[ 例 ] 设 n 个 球 随 机 放 入 N ( n ≤ N ) 个 盒 子 中 , 每 个 盒 子 可 放 任 意 多 个 球 , 求 ( 1 ) A = { 某 指 定 n 个 盒 子 各 有 一 球 } ( 2 ) B = { 恰 有 n 个 盒 子 各 有 一 球 } ( 1 ) P ( A ) = n ⋅ ( n − 1 ) ( n − 2 ) ⋯ 1 N n = n ! N n ( 2 ) P ( B ) = C N n ⋅ n ! N n [ 注 ] 类 比 : 12 个 人 , 每 个 人 在 365 天 出 生 等 可 能 ( 1 ) A = { 生 日 分 别 为 每 个 月 的 第 一 天 } ⟹ P ( A ) = 12 ! 36 5 12 ( 2 ) B = { 生 日 全 不 相 同 } ⟹ P ( B ) = C 365 12 ⋅ 12 ! 36 5 12 B ‾ = { 至 少 两 个 人 生 日 相 同 } ⟹ P ( B ‾ ) = 1 − P ( B ) \begin{aligned} \ [例]&\color{maroon}设n个球随机放入N(n\leq N)个盒子中,每个盒子可放任意多个球,求\\ &\color{maroon}(1)A=\{某指定n个盒子各有一球\}\\ &\color{maroon}(2)B=\{恰有n个盒子各有一球\}\\ &(1)P(A)=\frac{n\cdot(n-1)(n-2)\cdots1}{N^n}=\frac{n!}{N^n}\\ &(2)P(B)=\frac{C_N^n\cdot n!}{N^n}\\ [注]&类比:12个人,每个人在365天出生等可能\\ &(1)A=\{生日分别为每个月的第一天\}\implies P(A)=\frac{12!}{365^{12}}\\ &(2)B=\{生日全不相同\}\implies P(B)=\frac{C_{365}^{12}\cdot 12!}{365^{12}}\\ &\quad \overline{B}=\{至少两个人生日相同\}\implies P(\overline{B})=1-P(B)\\ \end{aligned} [例][注]设n个球随机放入N(n≤N)个盒子中,每个盒子可放任意多个球,求(1)A={某指定n个盒子各有一球}(2)B={恰有n个盒子各有一球}(1)P(A)=Nnn⋅(n−1)(n−2)⋯1=Nnn!(2)P(B)=NnCNn⋅n!类比:12个人,每个人在365天出生等可能(1)A={生日分别为每个月的第一天}⟹P(A)=3651212!(2)B={生日全不相同}⟹P(B)=36512C36512⋅12!B={至少两个人生日相同}⟹P(B)=1−P(B)
简单随机抽样
[ 例 ] 袋 中 有 5 个 球 , 3 白 2 黑 ( 1 ) 先 后 有 放 回 取 2 个 球 ( 2 ) 先 后 无 放 回 取 2 个 球 ( 3 ) 任 取 2 个 球 求 取 的 2 球 中 至 少 一 个 白 球 的 概 率 算 ‘ 两 球 全 黑 ’ , 用 总 数 减 去 它 ( 1 ) P 1 = 5 2 − 2 2 5 2 = 21 25 ( 2 ) P 2 = 5 ⋅ 4 − 2 ⋅ 1 5 ⋅ 4 = 9 10 ( 3 ) P 3 = C 5 2 − C 2 2 C 5 2 = 9 10 [ 注 ] ′ 先 后 无 放 回 取 k 个 球 ′ 与 ′ 任 取 k 个 球 ′ 概 率 相 等 , 后 者 好 算 \begin{aligned} \ [例]&\color{maroon}袋中有5个球,3白2黑\\ &\color{maroon}(1)先后有放回取2个球\\ &\color{maroon}(2)先后无放回取2个球\\ &\color{maroon}(3)任取2个球\\ &\color{maroon}求取的2球中至少一个白球的概率\\ &\color{maroon}算‘两球全黑’,用总数减去它\\ &(1)P_1=\frac{5^2-2^2}{5^2}=\frac{21}{25}\\ &(2)P_2=\frac{5\cdot4-2\cdot1}{5\cdot4}=\frac{9}{10}\\ &(3)P_3=\frac{C_5^2-C_2^2}{C_5^2}=\frac{9}{10}\\ [注]&'先后无放回取k个球'与'任取k个球'概率相等,后者好算\\ \end{aligned} [例][注]袋中有5个球,3白2黑(1)先后有放回取2个球(2)先后无放回取2个球(3)任取2个球求取的2球中至少一个白球的概率算‘两球全黑’,用总数减去它(1)P1=5252−22=2521(2)P2=5⋅45⋅4−2⋅1=109(3)P3=C52C52−C22=109′先后无放回取k个球′与′任取k个球′概率相等,后者好算
几何概型
[ 定 义 ] 若 Ω 是 一 个 可 度 量 的 几 何 区 域 , 且 样 本 点 落 入 Ω 中 的 某 一 可 度 量 子 区 域 A 的 可 能 性 大 小 与 A 的 几 何 度 量 成 正 比 , 而 与 A 的 位 置 、 形 状 无 关 , 称 为 几 何 概 型 , 即 P ( A ) = A 的 度 量 Ω 的 度 量 [ 引 例 ] 天 上 掉 馅 饼 于 操 场 上 , 拿 一 个 饭 盆 A 去 接 这 个 馅 饼 , P ( A ) = A 的 面 积 Ω 的 面 积 [ 例 ] 随 机 取 两 个 正 数 x , y , 这 两 个 数 中 的 每 一 个 都 不 超 过 1 , 求 x 与 y 之 和 不 超 过 1 , 积 不 小 于 0.09 的 概 率 . S A = ∫ 0.1 0.9 [ 1 − x − 0.09 x ] d x = 0.8 − x 2 2 ∣ 0.1 0.9 − 0.09 ln x ∣ 0.1 0.9 = 0.8 − 0.4 − 0.18 ⋅ ln 3 ≈ 0.2 P ( A ) = S A S Ω = 20 % \begin{aligned} \ [定义]&若\Omega是一个可度量的几何区域,且样本点落入\Omega中的某一可度量子区域A的可能性大小与A的几何度量成正比,\\ &而与A的位置、形状无关,称为几何概型,即P(A)=\frac{A的度量}{\Omega的度量}\\ [引例]&天上掉馅饼于操场上,拿一个饭盆A去接这个馅饼,P(A)=\frac{A的面积}{\Omega的面积}\\ [例]&\color{maroon}随机取两个正数x,y,这两个数中的每一个都不超过1,求x与y之和不超过1,积不小于0.09的概率.\\ &S_A=\int_{0.1}^{0.9}[1-x-\frac{0.09}{x}]dx=0.8-\frac{x^2}2|_{0.1}^{0.9}-0.09\ln x | _{0.1}^{0.9}=0.8-0.4-0.18\cdot\ln3\approx0.2\\ &P(A)=\frac{S_A}{S_\Omega}=20\% \end{aligned} [定义][引例][例]若Ω是一个可度量的几何区域,且样本点落入Ω中的某一可度量子区域A的可能性大小与A的几何度量成正比,而与A的位置、形状无关,称为几何概型,即P(A)=Ω的度量A的度量天上掉馅饼于操场上,拿一个饭盆A去接这个馅饼,P(A)=Ω的面积A的面积随机取两个正数x,y,这两个数中的每一个都不超过1,求x与y之和不超过1,积不小于0.09的概率.SA=∫0.10.9[1−x−x0.09]dx=0.8−2x2∣0.10.9−0.09lnx∣0.10.9=0.8−0.4−0.18⋅ln3≈0.2P(A)=SΩSA=20%
重要公式
[ 公 式 ] 1. 对 立 P ( A ) = 1 − P ( A ‾ ) 2. 减 法 P ( A B ‾ ) = P ( A − B ) = P ( A ) − P ( A B ) ( A 发 生 且 B 不 发 生 ) 3. 加 法 ( 1 ) P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) ( 2 ) P ( A + B + C ) = P ( A ) + P ( B ) + P ( C ) − P ( A B ) − P ( B C ) − P ( A C ) + P ( A B C ) [ 注 ] 1. 若 A 1 , A 2 , ⋯ , A n ( n > 3 ) 两 两 互 斥 ⟹ P ( ⋃ i = 1 n A i ) = ∑ i = 1 n P ( A i ) 2. 设 A 1 , A 2 , ⋯ , A n ( n > 3 ) , 若 对 其 中 任 意 有 限 个 A i 1 , A i 2 , ⋯ , A i k ( k ≥ 2 ) , 都 有 P ( A i 1 A i 2 ⋯ A i k ) = P ( A i 1 ) P ( A i 2 ) ⋯ P ( A i k ) ⟹ A 1 , A 2 , ⋯ , A n 相 互 独 立 且 ′ 夫 唱 妇 随 ′ , 即 : n 个 事 件 相 互 独 立 ⟺ A , B 独 立 ⟺ A ‾ , B ‾ 独 立 ⟺ A ‾ , B 独 立 ⟺ A , B ‾ 独 立 n = 3 , A 1 , A 2 , A 3 , 有 { P ( A 1 A 2 ) = P ( A 1 ) P ( A 2 ) P ( A 1 A 3 ) = P ( A 1 ) P ( A 3 ) P ( A 2 A 3 ) = P ( A 2 ) P ( A 3 ) P ( A 1 A 2 A 3 ) = P ( A 1 ) P ( A 2 ) P ( A 3 ) 相 互 独 立 若 上 者 只 成 立 前 三 条 , 则 称 为 两 两 独 立 于 是 若 A 1 , A 2 , ⋯ , A n 相 互 独 立 , 则 P ( ⋃ i = 1 n A i ) = 1 − P ( ⋃ i = 1 n A i ) = 1 − P ( ⋂ i = 1 n A i ‾ ) = 1 − ∏ i = 1 n [ 1 − P ( A i ) ] 即 A 1 ‾ , A 2 ‾ , ⋯ , A n ‾ 相 互 独 立 4. 条 件 概 率 P ( A ∣ B ) = P ( A B ) P ( B ) , P ( B ) > 0 5. 乘 法 P ( A B ) = { P ( B ) P ( A ∣ B ) , P ( B ) > 0 P ( A ) P ( B ∣ A ) , P ( A ) > 0 P ( A 1 A 2 A 3 ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) 6. 全 集 分 解 公 式 ( 全 概 率 公 式 ) [ 引 例 ] 一 个 村 子 有 且 仅 有 三 个 小 偷 A 1 , A 2 , A 3 , 求 P ( B ) = P { 失 窃 } 分 成 两 个 阶 段 { 1. 选 人 A 1 , A 2 , A 3 2. 去 偷 , B 则 P ( B ) = P ( B Ω ) = P ( B ∩ ( A 1 ∪ A 2 ∪ A 3 ) ) = P ( B A 1 ∪ B A 2 ∪ B A 3 ) = P ( B A 1 ) + P ( B A 2 ) + P ( B A 3 ) = P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) + P ( A 3 ) P ( B ∣ A 3 ) 故 P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) 7. 贝 叶 斯 公 式 ( 逆 概 率 公 式 ) 若 B 发 生 了 , 执 果 索 因 P ( A j ∣ B ) = P ( A j B ) P ( B ) = P ( A j ) P ( B ∣ A j ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) \begin{aligned} \ [公式]1.&对立\ P(A)=1-P(\overline{A})\\ 2.&减法\ P(A\overline{B})=P(A-B)=P(A)-P(AB)(A发生且B不发生)\\ 3.&加法\ (1)P(A+B)=P(A)+P(B)-P(AB)\\ &(2)P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)\\ &[注]\color{grey}1.若A_1,A_2,\cdots,A_n(n>3)两两互斥\implies P(\bigcup_{i=1}^nA_i)=\sum_{i=1}^nP(A_i)\\ &\color{grey}2.设A_1,A_2,\cdots,A_n(n>3),若对其中任意有限个A_{i1},A_{i2},\cdots,A_{ik}(k\geq2),\\ &\color{grey}都有P(A_{i1}A_{i2}\cdots A_{ik})=P(A_{i1})P(A_{i2})\cdots P(A_{ik})\implies A_1,A_2,\cdots,A_n相互独立\\ &\color{grey}且'夫唱妇随',即:n个事件相互独立\iff A,B独立\iff\overline{A},\overline{B}独立\iff\overline{A},B独立\iff A,\overline{B}独立\\ &\color{grey}n=3,A_1,A_2,A_3,有\begin{cases}P(A_1A_2)=P(A_1)P(A_2)\\P(A_1A_3)=P(A_1)P(A_3)\\P(A_2A_3)=P(A_2)P(A_3)\\P(A_1A_2A_3)=P(A_1)P(A_2)P(A_3)\end{cases}相互独立\\ &\color{grey}若上者只成立前三条,则称为两两独立\\ &\color{grey}于是若A_1,A_2,\cdots,A_n相互独立,则P(\bigcup_{i=1}^nA_i)=1-P(\bigcup_{i=1}^nA_i)=1-P(\bigcap_{i=1}^n\overline{A_i})=1-\prod_{i=1}^n[1-P(A_i)]\\ &\color{grey}即\overline{A_1},\overline{A_2},\cdots,\overline{A_n}相互独立\\ 4.&条件概率\ P(A\mid B)=\frac{P(AB)}{P(B)},P(B)>0\\ 5.&乘法\ P(AB)=\begin{cases}P(B)P(A\mid B),P(B)>0\\P(A)P(B\mid A),P(A)>0\end{cases}\\ &P(A_1A_2A_3)=P(A_1)P(A_2\mid A_1)P(A_3\mid A_1A_2)\\ 6.&全集分解公式(全概率公式)\\ &[引例]一个村子有且仅有三个小偷A_1,A_2,A_3,求P(B)=P\{失窃\}\\ &分成两个阶段\begin{cases}1.选人A_1,A_2,A_3\\2.去偷,B\end{cases}\\ &则P(B)=P(B\Omega)=P(B\cap(A_1\cup A_2\cup A_3))\\ &=P(BA_1\cup BA_2\cup BA_3)=P(BA_1)+P(BA_2)+P(BA_3)\\ &=P(A_1)P(B\mid A_1)+P(A_2)P(B\mid A_2)+P(A_3)P(B\mid A_3)\\ &故P(B)=\sum_{i=1}^nP(A_i)P(B\mid A_i)\\ 7.&贝叶斯公式(逆概率公式)\ 若B发生了,执果索因\\ &P(A_j\mid B)=\frac{P(A_jB)}{P(B)}=\frac{P(A_j)P(B\mid A_j)}{\sum_{i=1}^nP(A_i)P(B\mid A_i)} \end{aligned} [公式]1.2.3.4.5.6.7.对立 P(A)=1−P(A)减法 P(AB)=P(A−B)=P(A)−P(AB)(A发生且B不发生)加法 (1)P(A+B)=P(A)+P(B)−P(AB)(2)P(A+B+C)=P(A)+P(B)+P(C)−P(AB)−P(BC)−P(AC)+P(ABC)[注]1.若A1,A2,⋯,An(n>3)两两互斥⟹P(i=1⋃nAi)=i=1∑nP(Ai)2.设A1,A2,⋯,An(n>3),若对其中任意有限个Ai1,Ai2,⋯,Aik(k≥2),都有P(Ai1Ai2⋯Aik)=P(Ai1)P(Ai2)⋯P(Aik)⟹A1,A2,⋯,An相互独立且′夫唱妇随′,即:n个事件相互独立⟺A,B独立⟺A,B独立⟺A,B独立⟺A,B独立n=3,A1,A2,A3,有⎩⎪⎪⎪⎨⎪⎪⎪⎧P(A1A2)=P(A1)P(A2)P(A1A3)=P(A1)P(A3)P(A2A3)=P(A2)P(A3)P(A1A2A3)=P(A1)P(A2)P(A3)相互独立若上者只成立前三条,则称为两两独立于是若A1,A2,⋯,An相互独立,则P(i=1⋃nAi)=1−P(i=1⋃nAi)=1−P(i=1⋂nAi)=1−i=1∏n[1−P(Ai)]即A1,A2,⋯,An相互独立条件概率 P(A∣B)=P(B)P(AB),P(B)>0乘法 P(AB)={P(B)P(A∣B),P(B)>0P(A)P(B∣A),P(A)>0P(A1A2A3)=P(A1)P(A2∣A1)P(A3∣A1A2)全集分解公式(全概率公式)[引例]一个村子有且仅有三个小偷A1,A2,A3,求P(B)=P{失窃}分成两个阶段{1.选人A1,A2,A32.去偷,B则P(B)=P(BΩ)=P(B∩(A1∪A2∪A3))=P(BA1∪BA2∪BA3)=P(BA1)+P(BA2)+P(BA3)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+P(A3)P(B∣A3)故P(B)=i=1∑nP(Ai)P(B∣Ai)贝叶斯公式(逆概率公式) 若B发生了,执果索因P(Aj∣B)=P(B)P(AjB)=∑i=1nP(Ai)P(B∣Ai)P(Aj)P(B∣Aj)
[ 例 1 ] 以 下 结 论 , 错 误 的 是 ( D ) ? ( A ) 若 0 < P ( B ) < 1 , P ( A ∣ B ) + P ( A ‾ ∣ B ‾ ) = 1 ( B ) 若 A , B 满 足 P ( B ∣ A ) = 1 , 则 P ( A − B ) = 0 ( C ) ( A − B ) ∪ B = A ∪ B ( D ) 若 A , B 同 时 发 生 时 , C 必 发 生 , 则 P ( C ) < P ( A ) + P ( B ) − 1 ( A ) P ( A B ) P ( B ) + P ( A ‾ B ‾ ) P ( B ‾ ) = P ( A B ) P ( B ) + 1 − P ( A + B ) 1 − P ( B ) = P ( A B ) P ( B ) + 1 − P ( A ) − P ( B ) + P ( A B ) 1 − P ( B ) = P ( A B ) − P ( A B ) P ( B ) + P ( B ) − P ( A ) P ( B ) − [ P ( B ) ] 2 + P ( B ) P ( A B ) P ( B ) [ 1 − P ( B ) ] = 1 ⟹ P ( A B ) + P ( B ) − P ( A ) P ( B ) − [ P ( B ) ] 2 = P ( B ) − [ P ( B ) ] 2 ⟹ P ( A B ) = P ( A ) P ( B ) ( B ) P ( A B ) P ( A ) = 1 ⟹ P ( A B ) = P ( A ) ⟹ P ( A − B ) = P ( A ) − P ( A B ) = 0 ( C ) ( A B ‾ ) ∪ B = ( A ∩ B ‾ ) ∪ B = ( A ∪ B ) ∩ ( B ‾ ∪ B ) = A ∪ B ( D ) P ( A B ) ≤ P ( C ) ⟹ P ( A ) + P ( B ) − P ( A + B ) ≤ P ( C ) ⟹ P ( A ) + P ( B ) − P ( A + B ) ≥ P ( A ) + P ( B ) − 1 ⟹ P ( C ) ≥ P ( A ) + P ( B ) − 1 [ 例 2 ] 设 有 甲 、 乙 两 名 运 动 员 , 甲 命 中 目 标 的 概 率 为 0.6 , 乙 命 中 目 标 的 概 率 为 0.5 , 求 下 列 概 率 。 ( 1 ) 从 甲 、 乙 中 任 选 一 人 取 射 击 , 若 目 标 被 命 中 , 则 是 甲 命 中 的 概 率 是 多 少 ? ( 2 ) 甲 、 乙 各 自 独 立 射 击 , 若 目 标 被 命 中 , 则 是 甲 命 中 的 概 率 ? ( 1 ) 分 两 个 阶 段 { 1. 选 人 , A 甲 , A 乙 2. 射 击 , 命 中 = B P ( A 甲 ∣ B ) = P ( A 甲 ) P ( B ∣ A 甲 ) P ( A 甲 ) P ( B ∣ A 甲 ) + P ( A 乙 ) P ( B ∣ A 乙 ) = 1 2 ⋅ 0.6 1 2 ⋅ 0.6 + 1 2 ⋅ 0.5 = 6 11 ( 2 ) P ( A 甲 ∣ B ) = P ( A 甲 B ) P ( B ) = P ( A 甲 ) P ( A 甲 ) + P ( A 乙 ) − P ( A 甲 A 乙 ) = 0.6 0.6 + 0.5 − 0.6 ⋅ 0.5 = 3 4 [ 例 3 ] 每 箱 有 24 只 产 品 , 每 箱 含 0 , 1 , 2 件 残 品 的 箱 各 占 80 % , 15 % , 5 % , 现 随 机 抽 一 箱 , 随 即 检 验 其 中 4 只 , 若 未 发 现 残 品 则 通 过 验 收 , 否 则 要 逐 一 检 验 并 更 换 , 求 ( 1 ) 一 次 通 过 验 收 的 概 率 ( 2 ) 通 过 验 收 的 箱 中 确 无 残 品 的 概 率 ( 1 ) 记 A i = { 抽 取 的 一 箱 中 含 i 件 残 品 } . i = 0 , 1 , 2. 但 P ( A 0 ) = 0.8 , P ( A 1 ) = 0.15 , P ( A 2 ) = 0.05 分 阶 段 { 1. 取 箱 子 2. 取 4 只 检 验 , 收 为 B o r 不 收 为 B ‾ P ( B ) = P ( A 0 ) P ( B ∣ A 0 ) + P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) = 0.8 ⋅ 1 + 0.15 ⋅ C 23 4 C 24 4 + 0.05 ⋅ C 22 4 C 24 4 ≈ 0.96 ( 2 ) P ( A 0 ∣ B ) = 0.8 0.96 ≈ 0.83 \begin{aligned} \ [例1]&\color{maroon}以下结论,错误的是(D)?\\ &\color{maroon}(A)若0< P(B)< 1,P(A\mid B)+P(\overline{A}\mid\overline{B})=1\\ &\color{maroon}(B)若A,B满足P(B\mid A)=1,则P(A-B)=0\\ &\color{maroon}(C)(A-B)\cup B=A\cup B\\ &\color{maroon}(D)若A,B同时发生时,C必发生,则P(C)< P(A)+P(B)-1\\ &(A)\ \frac{P(AB)}{P(B)}+\frac{P(\overline{A}\overline{B})}{P(\overline{B})}=\frac{P(AB)}{P(B)}+\frac{1-P(A+B)}{1-P(B)}=\frac{P(AB)}{P(B)}+\frac{1-P(A)-P(B)+P(AB)}{1-P(B)}\\ &=\frac{P(AB)-P(AB)P(B)+P(B)-P(A)P(B)-[P(B)]^2+P(B)P(AB)}{P(B)[1-P(B)]}=1\\ &\implies P(AB)+P(B)-P(A)P(B)-[P(B)]^2=P(B)-[P(B)]^2\implies P(AB)=P(A)P(B)\\ &(B)\ \frac{P(AB)}{P(A)}=1\implies P(AB)=P(A)\\ &\implies P(A-B)=P(A)-P(AB)=0\\ &(C)\ (A\overline{B})\cup B=(A\cap \overline{B})\cup B=(A\cup B)\cap(\overline{B}\cup B)=A\cup B\\ &(D)\ P(AB)\leq P(C)\implies P(A)+P(B)-P(A+B)\leq P(C)\\ &\implies P(A)+P(B)-P(A+B)\geq P(A)+P(B)-1\implies P(C)\geq P(A)+P(B)-1\\ [例2]&\color{maroon}设有甲、乙两名运动员,甲命中目标的概率为0.6,乙命中目标的概率为0.5,求下列概率。\\ &\color{maroon}(1)从甲、乙中任选一人取射击,若目标被命中,则是甲命中的概率是多少?\\ &\color{maroon}(2)甲、乙各自独立射击,若目标被命中,则是甲命中的概率?\\ &(1)分两个阶段\begin{cases}1.选人,A_甲,A_乙\\2.射击,命中=B\end{cases}\\ &P(A_甲\mid B)=\frac{P(A_甲)P(B\mid A_甲)}{P(A_甲)P(B\mid A_甲)+P(A_乙)P(B\mid A_乙)}\\ &=\frac{\frac12\cdot0.6}{\frac12\cdot0.6+\frac12\cdot0.5}=\frac6{11}\\ &(2)P(A_甲\mid B)=\frac{P(A_甲B)}{P(B)}=\frac{P(A_甲)}{P(A_甲)+P(A_乙)-P(A_甲A_乙)}=\frac{0.6}{0.6+0.5-0.6\cdot0.5}=\frac34\\ [例3]&\color{maroon}每箱有24只产品,每箱含0,1,2件残品的箱各占80\%, 15\%, 5\%,现随机抽一箱,随即检验其中4只,\\ &\color{maroon}若未发现残品则通过验收,否则要逐一检验并更换,求\\ &\color{maroon}(1)一次通过验收的概率\\ &\color{maroon}(2)通过验收的箱中确无残品的概率\\ &(1)记A_i=\{抽取的一箱中含i件残品\}.i=0,1,2.\\ &但P(A_0)=0.8,P(A_1)=0.15,P(A_2)=0.05\\ &分阶段\begin{cases}1.取箱子\\2.取4只检验,收为Bor不收为\overline{B}\end{cases}\\ &P(B)=P(A_0)P(B\mid A_0)+P(A_1)P(B\mid A_1)+P(A_2)P(B\mid A_2)\\ &=0.8\cdot1+0.15\cdot\frac{C_{23}^4}{C_{24}^4}+0.05\cdot\frac{C_{22}^4}{C_{24}^4}\approx0.96\\ &(2)P(A_0\mid B)=\frac{0.8}{0.96}\approx0.83 \end{aligned} [例1][例2][例3]以下结论,错误的是(D)?(A)若0<P(B)<1,P(A∣B)+P(A∣B)=1(B)若A,B满足P(B∣A)=1,则P(A−B)=0(C)(A−B)∪B=A∪B(D)若A,B同时发生时,C必发生,则P(C)<P(A)+P(B)−1(A) P(B)P(AB)+P(B)P(AB)=P(B)P(AB)+1−P(B)1−P(A+B)=P(B)P(AB)+1−P(B)1−P(A)−P(B)+P(AB)=P(B)[1−P(B)]P(AB)−P(AB)P(B)+P(B)−P(A)P(B)−[P(B)]2+P(B)P(AB)=1⟹P(AB)+P(B)−P(A)P(B)−[P(B)]2=P(B)−[P(B)]2⟹P(AB)=P(A)P(B)(B) P(A)P(AB)=1⟹P(AB)=P(A)⟹P(A−B)=P(A)−P(AB)=0(C) (AB)∪B=(A∩B)∪B=(A∪B)∩(B∪B)=A∪B(D) P(AB)≤P(C)⟹P(A)+P(B)−P(A+B)≤P(C)⟹P(A)+P(B)−P(A+B)≥P(A)+P(B)−1⟹P(C)≥P(A)+P(B)−1设有甲、乙两名运动员,甲命中目标的概率为0.6,乙命中目标的概率为0.5,求下列概率。(1)从甲、乙中任选一人取射击,若目标被命中,则是甲命中的概率是多少?(2)甲、乙各自独立射击,若目标被命中,则是甲命中的概率?(1)分两个阶段{1.选人,A甲,A乙2.射击,命中=BP(A甲∣B)=P(A甲)P(B∣A甲)+P(A乙)P(B∣A乙)P(A甲)P(B∣A甲)=21⋅0.6+21⋅0.521⋅0.6=116(2)P(A甲∣B)=P(B)P(A甲B)=P(A甲)+P(A乙)−P(A甲A乙)P(A甲)=0.6+0.5−0.6⋅0.50.6=43每箱有24只产品,每箱含0,1,2件残品的箱各占80%,15%,5%,现随机抽一箱,随即检验其中4只,若未发现残品则通过验收,否则要逐一检验并更换,求(1)一次通过验收的概率(2)通过验收的箱中确无残品的概率(1)记Ai={抽取的一箱中含i件残品}.i=0,1,2.但P(A0)=0.8,P(A1)=0.15,P(A2)=0.05分阶段{1.取箱子2.取4只检验,收为Bor不收为BP(B)=P(A0)P(B∣A0)+P(A1)P(B∣A1)+P(A2)P(B∣A2)=0.8⋅1+0.15⋅C244C234+0.05⋅C244C224≈0.96(2)P(A0∣B)=0.960.8≈0.83
一维随机变量及其分布
随机变量与分布函数
( 1 ) r , v ( 随 机 变 量 ) 定 义 在 Ω = { ω } 上 , 取 值 在 实 数 轴 上 的 变 量 。 即 X = X ( ω ) , ω ∈ Ω ( 2 ) 分 布 函 数 F ( x ) = P { X ≤ x } , 其 中 − ∞ < x < + ∞ . \begin{aligned} &(1)r,v(随机变量)\quad 定义在\Omega=\{\omega\}上,取值在实数轴上的变量。即X=X(\omega),\omega\in\Omega\\ &(2)分布函数F(x)=P\{X\leq x\},其中-\infty< x<+\infty. \end{aligned} (1)r,v(随机变量)定义在Ω={ω}上,取值在实数轴上的变量。即X=X(ω),ω∈Ω(2)分布函数F(x)=P{X≤x},其中−∞<x<+∞.
离散型随机变量
[ 定 义 ] x 取 有 限 个 或 无 穷 可 列 个 值 [ 分 布 律 ] x ∼ ( x 1 x 2 ⋯ x n ⋯ P 1 P 2 ⋯ P n ⋯ ) F ( x ) = P { X ≤ x } , 离 散 型 r , v ⟺ 步 步 高 的 阶 梯 形 函 数 \begin{aligned} \ [定义]&x取有限个或无穷可列个值\\ [分布律]&x\sim\begin{pmatrix}x_1&x_2&\cdots&x_n&\cdots\\P_1&P_2&\cdots&P_n&\cdots\end{pmatrix}\\ &F(x)=P\{X\leq x\},离散型r,v\iff 步步高的阶梯形函数\\ \end{aligned} [定义][分布律]x取有限个或无穷可列个值x∼(x1P1x2P2⋯⋯xnPn⋯⋯)F(x)=P{X≤x},离散型r,v⟺步步高的阶梯形函数
连续型随机变量
[ 定 义 ] 若 存 在 非 负 可 积 函 数 f ( x ) , 使 得 ∀ x ∈ ( − ∞ , + ∞ ) , 有 F ( x ) = ∫ − ∞ x f ( t ) d t , 则 称 x 为 连 续 型 r , v . f ( x ) 叫 概 率 密 度 [ 注 ] F ( x ) = P { X ≤ x } = { ∫ − ∞ x f ( t ) d t , 连 续 型 ∑ x i ≤ x P i , 离 散 型 \begin{aligned} \ [定义]&若存在非负可积函数f(x),使得\forall x\in(-\infty,+\infty),有F(x)=\int_{-\infty}^xf(t)dt,则称x为连续型r,v.f(x)叫概率密度\\ [注]&F(x)=P\{X\leq x\}=\begin{cases}\int_{-\infty}^xf(t)dt,连续型\\\sum_{x_i\leq x}P_i,离散型\end{cases}\\ \end{aligned} [定义][注]若存在非负可积函数f(x),使得∀x∈(−∞,+∞),有F(x)=∫−∞xf(t)dt,则称x为连续型r,v.f(x)叫概率密度F(x)=P{X≤x}={∫−∞xf(t)dt,连续型∑xi≤xPi,离散型
X~F(x)
X ∼ F ( x ) { P i → 分 布 律 f ( x ) → 概 率 密 度 ( 1 ) F ( x ) 是 某 个 X 的 分 布 函 数 ⟺ { 1. 单 调 不 减 2. F ( − ∞ ) = 0 , F ( + ∞ ) = 1 3. 右 连 续 ( 等 号 跟 着 大 于 号 ) ( 2 ) { P i } 是 分 布 律 ⟺ { 1. P i ≥ 0 2. ∑ i P i = 1 ( 3 ) f ( x ) 是 概 率 密 度 ⟺ { 1. f ( x ) ≥ 0 2. ∫ − ∞ + ∞ f ( x ) d x = 1 \begin{aligned} &X\sim F(x)\begin{cases}P_i\to分布律\\f(x)\to概率密度\end{cases}\\ &(1)F(x)是某个X的分布函数\iff\begin{cases}1.单调不减\\2.F(-\infty)=0,F(+\infty)=1\\3.右连续(等号跟着大于号)\end{cases}\\ &(2)\{P_i\}是分布律\iff\begin{cases}1.P_i\geq0\\2.\sum_iP_i=1\end{cases}\\ &(3)f(x)是概率密度\iff\begin{cases}1.f(x)\geq0\\2.\int_{-\infty}^{+\infty}f(x)dx=1\end{cases}\\ \end{aligned} X∼F(x){Pi→分布律f(x)→概率密度(1)F(x)是某个X的分布函数⟺⎩⎪⎨⎪⎧1.单调不减2.F(−∞)=0,F(+∞)=13.右连续(等号跟着大于号)(2){Pi}是分布律⟺{1.Pi≥02.∑iPi=1(3)f(x)是概率密度⟺{1.f(x)≥02.∫−∞+∞f(x)dx=1
八个常见分布
( 1 ) − ( 5 ) 离 散 型 ( 6 ) − ( 8 ) 连 续 型 ( 1 ) 0 − 1 分 布 X ∼ ( 1 0 P 1 − P ) ( 2 ) 二 项 分 布 { 1. 独 立 2. P ( A ) = P 3. 只 有 A , A ‾ , 非 白 即 黑 记 X 为 A 发 生 的 次 数 , P { x = k } = C n k P k ( 1 − P ) n − k , k = 0 , 1 , ⋯ , n ⟹ X ∼ B ( n , P ) ( 3 ) 几 何 分 布 与 几 何 无 关 , 首 中 即 停 止 , 记 X 为 试 验 次 数 ⟹ P { x = k } = P 1 ( 1 − P ) k − 1 , k = 1 , 2 , ⋯ ( 4 ) 超 几 何 分 布 古 典 概 型 , 设 N 件 产 品 , M 、 件 正 品 , N − M 件 次 品 , 无 放 回 取 n 次 , 则 P { x = k } = C M k C N − M n − k C N n ( 5 ) 泊 松 分 布 某 时 间 段 内 , 某 场 合 下 , 源 源 不 断 的 质 点 来 流 的 个 数 , 也 常 用 于 描 述 稀 有 事 件 的 P P { X = k } = λ k k ! e − λ , { λ − − 强 度 k = 0 , 1 , ⋯ ( 6 ) 均 匀 分 布 对 比 几 何 概 型 , 若 X ∼ f ( x ) = { 1 b − a , a ≤ x ≤ b 0 , 其 他 , 称 X ∼ U [ a , b ] [ 注 ] 高 档 次 说 法 : “ X 在 I 上 的 任 意 子 区 间 取 值 的 概 率 与 该 子 区 间 长 度 成 正 比 ” → X ∼ U ( I ) ( 7 ) 指 数 分 布 X ∼ f ( x ) = { λ e − λ x , x > 0 0 , x ≤ 0 , 称 X ∼ E ( λ ) , λ − − 失 效 率 [ 注 ] 无 记 忆 性 P { X ≥ t + s ∣ X ≥ t } = P { x ≥ s } F ( x ) = P { X ≤ x } = ∫ − ∞ x f ( t ) d t = { 1 − e − λ x , x ≥ 0 0 , x < 0 { 几 何 分 布 , 离 散 性 等 待 分 布 指 数 分 布 , 连 续 性 等 待 分 布 ( 8 ) 正 态 分 布 X ∼ f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ < x < + ∞ [ 注 ] 若 μ = 0 , σ 2 = 1 ⟹ X ∼ N ( 0 , 1 ) X ∼ φ ( x ) = 1 2 π e − x 2 2 X ∼ Φ ( x ) = ∫ − ∞ x 1 2 π e − t 2 2 d t \begin{aligned} &(1)-(5)离散型\quad(6)-(8)连续型\\ (1)&0-1分布\quad X\sim\begin{pmatrix}1&0\\P&1-P\end{pmatrix}\\ (2)&二项分布\quad \begin{cases}1.独立\\2.P(A)=P\\3.只有A,\overline{A},非白即黑\end{cases}\\ &记X为A发生的次数,P\{x=k\}=C_n^kP^k(1-P)^{n-k},k=0,1,\cdots,n\\ &\implies X\sim B(n,P)\\ (3)&几何分布\quad 与几何无关,首中即停止,记X为试验次数\implies P\{x=k\}=P^1(1-P)^{k-1},k=1,2,\cdots\\ (4)&超几何分布\quad 古典概型,设N件产品,M、件正品,N-M件次品,无放回取n次,则P\{x=k\}=\frac{C_M^kC_{N-M}^{n-k}}{C_N^n}\\ (5)&泊松分布\quad某时间段内,某场合下,源源不断的质点来流的个数,也常用于描述稀有事件的P\\ &P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda},\begin{cases}\lambda--强度\\k=0,1,\cdots\end{cases}\\ (6)&均匀分布\quad 对比几何概型,若X\sim f(x)=\begin{cases}\frac1{b-a},a\leq x\leq b\\0,其他\end{cases},称X\sim U[a,b]\\ &[注]高档次说法:“X在I上的任意子区间取值的概率与该子区间长度成正比”\to X\sim U(I)\\ (7)&指数分布\quad X\sim f(x)=\begin{cases}\lambda e^{-\lambda x},x>0\\0,x\leq0\end{cases},称X\sim E(\lambda),\lambda--失效率\\ &[注]无记忆性\ P\{X\geq t+s\mid X\geq t\}=P\{x\geq s\}\\ &F(x)=P\{X\leq x\}=\int_{-\infty}^xf(t)dt=\begin{cases}1-e^{-\lambda x},x\geq0\\0,x< 0\end{cases}\\ &\begin{cases}几何分布,离散性等待分布\\指数分布,连续性等待分布\end{cases}\\ (8)&正态分布\quad X\sim f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},-\infty< x< +\infty\\ &[注]若\mu=0,\sigma^2=1\implies X\sim N(0,1)\\ &X\sim\varphi(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}2}\\ &X\sim\Phi(x)=\int_{-\infty}^x\frac1{\sqrt{2\pi}}e^{-\frac{t^2}2}dt\\ \end{aligned} (1)(2)(3)(4)(5)(6)(7)(8)(1)−(5)离散型(6)−(8)连续型0−1分布X∼(1P01−P)二项分布⎩⎪⎨⎪⎧1.独立2.P(A)=P3.只有A,A,非白即黑记X为A发生的次数,P{x=k}=CnkPk(1−P)n−k,k=0,1,⋯,n⟹X∼B(n,P)几何分布与几何无关,首中即停止,记X为试验次数⟹P{x=k}=P1(1−P)k−1,k=1,2,⋯超几何分布古典概型,设N件产品,M、件正品,N−M件次品,无放回取n次,则P{x=k}=CNnCMkCN−Mn−k泊松分布某时间段内,某场合下,源源不断的质点来流的个数,也常用于描述稀有事件的PP{X=k}=k!λke−λ,{λ−−强度k=0,1,⋯均匀分布对比几何概型,若X∼f(x)={b−a1,a≤x≤b0,其他,称X∼U[a,b][注]高档次说法:“X在I上的任意子区间取值的概率与该子区间长度成正比”→X∼U(I)指数分布X∼f(x)={λe−λx,x>00,x≤0,称X∼E(λ),λ−−失效率[注]无记忆性 P{X≥t+s∣X≥t}=P{x≥s}F(x)=P{X≤x}=∫−∞xf(t)dt={1−e−λx,x≥00,x<0{几何分布,离散性等待分布指数分布,连续性等待分布正态分布X∼f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<+∞[注]若μ=0,σ2=1⟹X∼N(0,1)X∼φ(x)=2π1e−2x2X∼Φ(x)=∫−∞x2π1e−2t2dt
[ 例 1 ] 设 X ∼ F ( x ) , f ( x ) = a f 1 ( x ) + b f 2 ( x ) , f 1 ( x ) ∼ N ( 0 , σ 2 ) , f 2 ( x ) ∼ E ( λ ) F ( 0 ) = 1 8 , 则 a = ‾ , b = ‾ 1. ∫ − ∞ + ∞ f ( x ) d x = a ∫ − ∞ + ∞ f 1 ( x ) d x + b ∫ − ∞ + ∞ f 2 ( x ) d x ⟹ 1 = a + b 2. F ( 0 ) = ∫ − ∞ 0 f ( x ) d x = a ∫ − ∞ 0 f 1 ( x ) d x + b ∫ − ∞ 0 f 2 ( x ) d x = 1 8 即 a ⋅ 1 2 + b ⋅ 0 = 1 8 ⟹ a = 1 4 ⟹ b = 3 4 [ 例 2 ] X ∼ f ( x ) = { A e − x , x > λ 0 , 其 他 , λ > 0 , P { λ < X < λ + a } ( a > 0 ) 的 值 ∫ − ∞ + ∞ f ( x ) d x = 1 ⟹ ∫ λ + ∞ A e − x d x = 1 ⟹ A ⋅ e − x ∣ + ∞ λ = A e − λ = 1 ⟹ A = e λ ⟹ P { λ < X < λ + a } = ∫ λ λ + a e λ ⋅ e − x d x = e λ [ e − x ] ∣ λ + a λ = e λ ⋅ ( e − λ − e − ( λ + a ) ) = 1 − e − a 故 其 值 与 λ 无 关 , 随 着 a 的 增 大 其 概 率 增 大 [ 例 3 ] X ∼ E ( λ ) , 对 X 作 三 次 独 立 重 复 观 察 , 至 少 有 一 次 观 测 值 大 于 2 的 概 率 为 7 8 , 则 λ = ‾ 记 Y = { 对 X 作 三 次 独 立 重 复 观 察 中 观 测 值 大 于 2 发 生 的 次 数 } ⟹ Y ∼ B ( 3 , P ) 其 中 P = { X > 2 } = ∫ 2 + ∞ f ( x ) d x = 1 − P { X ≤ 2 } = 1 − F ( 2 ) = 1 − [ 1 − e − 2 λ ] = e − 2 λ 由 题 意 , 得 P { Y ≥ 1 } = 7 8 = 1 − P { Y = 0 } = 1 − ( 1 − P ) 3 = 1 − ( 1 − e − 2 λ ) 3 ⟹ e − 2 λ = 1 2 ⟹ λ = − 1 2 ln 1 2 = 1 2 ln 2 [ 例 4 ] X ∼ E ( λ ) 求 Y = 1 − e − λ x ∼ f Y ( y ) X ∼ f X ( x ) , Y = g ( X ) , 求 f Y ( y ) 1. F Y ( y ) = P { Y ≤ y } = P { g ( X ) ≤ y } = P { X ∈ I y } = ∫ I y f x ( x ) d x 2. f Y ( y ) = F Y ′ ( y ) 1. F Y ( y ) = P { Y ≤ y } = P { 1 − e − λ x ≤ y } ( 1 ) y < 0 ⟹ F Y ( y ) = 0 ( 2 ) y ≥ 1 ⟹ F Y ( y ) = 1 ( 3 ) 0 ≤ y ≤ 1 ⟹ F Y ( y ) = P { 0 ≤ X ≤ − 1 λ ln ( 1 − y ) } = F X ( − 1 λ ln ( 1 − y ) ) = 1 − e − λ [ − 1 λ ln ( 1 − y ) ] 2. f Y ( y ) = { 1 , 0 ≤ y < 1 0 , 其 他 \begin{aligned} \ [例1]&\color{maroon}设X\sim F(x),f(x)=af_1(x)+bf_2(x),f_1(x)\sim N(0,\sigma^2),f_2(x)\sim E(\lambda)\\ &\color{maroon}F(0)=\frac18,则a=\underline{\quad},b=\underline{\quad}\\ &1.\int_{-\infty}^{+\infty}f(x)dx=a\int_{-\infty}^{+\infty}f_1(x)dx+b\int_{-\infty}^{+\infty}f_2(x)dx\implies 1=a+b\\ &2.F(0)=\int_{-\infty}^0f(x)dx=a\int_{-\infty}^{0}f_1(x)dx+b\int_{-\infty}^{0}f_2(x)dx=\frac18\\ &即a\cdot\frac12+b\cdot0=\frac18\implies a=\frac14\implies b=\frac34\\ [例2]&\color{maroon}X\sim f(x)=\begin{cases}Ae^{-x},x>\lambda\\0,其他\end{cases},\lambda>0,P\{\lambda< X< \lambda+a\}(a>0)的值\\ &\int_{-\infty}^{+\infty}f(x)dx=1\implies \int_{\lambda}^{+\infty}Ae^{-x}dx=1\implies A\cdot e^{-x}\mid^\lambda_{+\infty}=Ae^{-\lambda}=1\implies A=e^{\lambda}\\ &\implies P\{\lambda< X< \lambda+a\}=\int_{\lambda}^{\lambda+a}e^{\lambda}\cdot e^{-x}dx=e^{\lambda}[e^{-x}]\mid^{\lambda}_{\lambda+a}=e^{\lambda}\cdot(e^{-\lambda}-e^{-(\lambda+a)})=1-e^{-a}\\ &故其值与\lambda无关,随着a的增大其概率增大\\ [例3]&\color{maroon}X\sim E(\lambda),对X作三次独立重复观察,至少有一次观测值大于2的概率为\frac78,则\lambda=\underline{\quad}\\ &记Y=\{对X作三次独立重复观察中观测值大于2发生的次数\}\implies Y\sim B(3,P)\\ &其中P=\{X>2\}=\int_2^{+\infty}f(x)dx=1-P\{X\leq2\}=1-F(2)=1-[1-e^{-2\lambda}]=e^{-2\lambda}\\ &由题意,得P\{Y\geq1\}=\frac78=1-P\{Y=0\}=1-(1-P)^3=1-(1-e^{-2\lambda})^3\\ &\implies e^{-2\lambda}=\frac12\implies \lambda=-\frac12\ln\frac12=\frac12\ln2\\ [例4]&\color{maroon}X\sim E(\lambda)求Y=1-e^{-\lambda x}\sim f_Y(y)\\ &X\sim f_X(x),Y=g(X),求f_Y(y)\\ &1.F_Y(y)=P\{Y\leq y\}=P\{g(X)\leq y\}=P\{X\in I_y\}=\int_{I_y}f_x(x)dx\\ &2.f_Y(y)=F_Y'(y)\\ &1.F_Y(y)=P\{Y\leq y\}=P\{1-e^{-\lambda x}\leq y\}\\ &(1)y< 0\implies F_Y(y)=0\\ &(2)y\geq1\implies F_Y(y)=1\\ &(3)0\leq y\leq1\implies F_Y(y)=P\{0\leq X\leq -\frac1{\lambda}\ln(1-y)\}=F_X(-\frac1{\lambda}\ln(1-y))=1-e^{-\lambda[-\frac1{\lambda}\ln(1-y)]}\\ &2.f_Y(y)=\begin{cases}1,0\leq y< 1\\0,其他\end{cases}\\ \end{aligned} [例1][例2][例3][例4]设X∼F(x),f(x)=af1(x)+bf2(x),f1(x)∼N(0,σ2),f2(x)∼E(λ)F(0)=81,则a=,b=1.∫−∞+∞f(x)dx=a∫−∞+∞f1(x)dx+b∫−∞+∞f2(x)dx⟹1=a+b2.F(0)=∫−∞0f(x)dx=a∫−∞0f1(x)dx+b∫−∞0f2(x)dx=81即a⋅21+b⋅0=81⟹a=41⟹b=43X∼f(x)={Ae−x,x>λ0,其他,λ>0,P{λ<X<λ+a}(a>0)的值∫−∞+∞f(x)dx=1⟹∫λ+∞Ae−xdx=1⟹A⋅e−x∣+∞λ=Ae−λ=1⟹A=eλ⟹P{λ<X<λ+a}=∫λλ+aeλ⋅e−xdx=eλ[e−x]∣λ+aλ=eλ⋅(e−λ−e−(λ+a))=1−e−a故其值与λ无关,随着a的增大其概率增大X∼E(λ),对X作三次独立重复观察,至少有一次观测值大于2的概率为87,则λ=记Y={对X作三次独立重复观察中观测值大于2发生的次数}⟹Y∼B(3,P)其中P={X>2}=∫2+∞f(x)dx=1−P{X≤2}=1−F(2)=1−[1−e−2λ]=e−2λ由题意,得P{Y≥1}=87=1−P{Y=0}=1−(1−P)3=1−(1−e−2λ)3⟹e−2λ=21⟹λ=−21ln21=21ln2X∼E(λ)求Y=1−e−λx∼fY(y)X∼fX(x),Y=g(X),求fY(y)1.FY(y)=P{Y≤y}=P{g(X)≤y}=P{X∈Iy}=∫Iyfx(x)dx2.fY(y)=FY′(y)1.FY(y)=P{Y≤y}=P{1−e−λx≤y}(1)y<0⟹FY(y)=0(2)y≥1⟹FY(y)=1(3)0≤y≤1⟹FY(y)=P{0≤X≤−λ1ln(1−y)}=FX(−λ1ln(1−y))=1−e−λ[−λ1ln(1−y)]2.fY(y)={1,0≤y<10,其他
多元随机变量及其分布
概念
1. 联 合 分 布 设 ( X , Y ) , F ( x , y ) = P { X ≤ x , Y ≤ y } , − ∞ < x < + ∞ , − ∞ < y < + ∞ 2. 边 缘 分 布 F X ( x ) = lim y → + ∞ F ( x , y ) , F Y ( y ) = lim x → + ∞ F ( x , y ) [ 注 ] 1. 离 散 型 ( X , Y ) ∼ P i j ( 联 合 分 布 律 ) 条 件 分 布 为 P ( X = x i ∣ Y = y i ) = P ( X = x i , Y = y j ) P ( Y = y j ) = P i j P ⋅ j P ( X = 1 ∣ Y = 0 ) = P 21 P ⋅ 1 条 件 = 联 合 边 缘 2. 连 续 型 ( X , Y ) ∼ f ( x , y ) ( 联 合 概 率 密 度 ) 边 缘 密 度 为 f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y , f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x 条 件 密 度 为 f X ∣ Y ( x ∣ y ) = f ( x , y ) f Y ( y ) 无 论 离 散 还 是 连 续 , 条 件 = 联 合 边 缘 3. 独 立 性 设 ( X , Y ) , X , Y 独 立 ⟺ F ( x , y ) = F X ( x ) ⋅ F Y ( y ) ⟺ P i j = P i ⋅ ⋅ P ⋅ j , ∀ i , j ⟺ f ( x , y ) = f X ( x ) ⋅ f Y ( y ) 4. 两 个 分 布 ( 1 ) 均 匀 分 布 ( X , Y ) ∼ f ( x , y ) = { 1 S D , ( x , y ) ∈ D 0 , ( x , y ) ∉ D ( 2 ) 正 态 分 布 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) 其 中 E X = μ 1 , E Y = μ 2 , D X = σ 1 2 , D Y = σ 2 2 , ϱ x y = ρ \begin{aligned} 1.&联合分布\quad 设(X,Y),F(x,y)=P\{X\leq x,Y\leq y\},-\infty< x<+\infty,-\infty< y<+\infty\\ 2.&边缘分布\quad F_X(x)=\lim_{y\to+\infty}F(x,y),F_Y(y)=\lim_{x\to+\infty}F(x,y)\\ [注]&1.离散型(X,Y)\sim P_{ij}(联合分布律)\\ &条件分布为P(X=x_i\mid Y=y_i)=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}=\frac{P_{ij}}{P_{\cdot j}}\\ &P(X=1\mid Y=0)=\frac{P_{21}}{P_{\cdot 1}}\\ &条件=\frac{联合}{边缘}\\ &2.连续型(X,Y)\sim f(x,y)(联合概率密度)\\ &边缘密度为f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy,f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx\\ &条件密度为f_{X\mid Y}(x\mid y)=\frac{f(x,y)}{f_Y(y)}\\ &无论离散还是连续,条件=\frac{联合}{边缘}\\ 3.&独立性\quad 设(X,Y),X,Y独立\iff F(x,y)=F_X(x)\cdot F_Y(y)\\ &\iff P_{ij}=P_{i\cdot}\cdot P_{\cdot j},\forall i,j\\ &\iff f(x,y)=f_X(x)\cdot f_Y(y)\\ 4.&两个分布\\ &(1)均匀分布\quad (X,Y)\sim f(x,y)=\begin{cases}\frac1{S_D},(x,y)\in D\\0,(x,y)\notin D\end{cases}\\ &(2)正态分布\quad (X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\\ &其中EX=\mu_1,EY=\mu_2,DX=\sigma_1^2,DY=\sigma_2^2,\varrho_{xy}=\rho\\ \end{aligned} 1.2.[注]3.4.联合分布设(X,Y),F(x,y)=P{X≤x,Y≤y},−∞<x<+∞,−∞<y<+∞边缘分布FX(x)=y→+∞limF(x,y),FY(y)=x→+∞limF(x,y)1.离散型(X,Y)∼Pij(联合分布律)条件分布为P(X=xi∣Y=yi)=P(Y=yj)P(X=xi,Y=yj)=P⋅jPijP(X=1∣Y=0)=P⋅1P21条件=边缘联合2.连续型(X,Y)∼f(x,y)(联合概率密度)边缘密度为fX(x)=∫−∞+∞f(x,y)dy,fY(y)=∫−∞+∞f(x,y)dx条件密度为fX∣Y(x∣y)=fY(y)f(x,y)无论离散还是连续,条件=边缘联合独立性设(X,Y),X,Y独立⟺F(x,y)=FX(x)⋅FY(y)⟺Pij=Pi⋅⋅P⋅j,∀i,j⟺f(x,y)=f