聚类之DBSCAN算法(递归实现)
文章目录
- 前言
- 1. 基本概念
- 2. 算法流程
- 3. 代码实现
- 结束语
前言
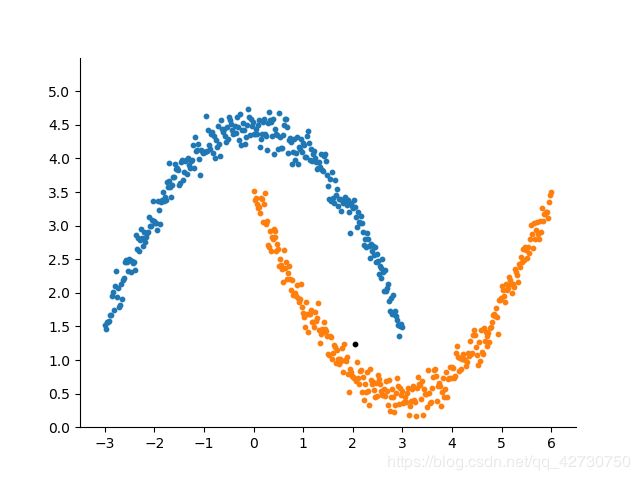
前面介绍的K-Means、K-Means++和Mean Shift算法都是基于距离的聚类算法,它们聚类的结果基本上都是球状的簇,也就是前面几篇博客的聚类结果。如果数据集的聚类结果是非球状时,基于距离的聚类效果并不好,而基于密度的聚类算法能够较好地处理非球状结构的数据,而且能处理任意形状的聚类。如下图所示。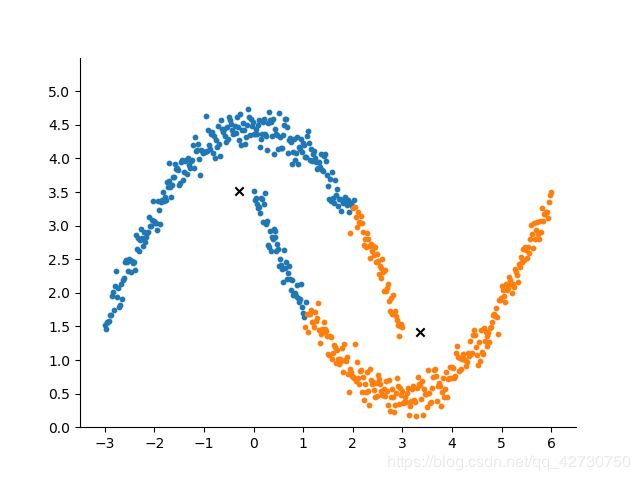 通常情况下,密度聚类算法从样本密度的角度 ( ( (假设聚类结构能通过样本分布的紧密程度来确定 ) ) )来考察样本之间的可连续性,并基于可连续样本不断扩展聚类簇以获得最终的聚类结果。
通常情况下,密度聚类算法从样本密度的角度 ( ( (假设聚类结构能通过样本分布的紧密程度来确定 ) ) )来考察样本之间的可连续性,并基于可连续样本不断扩展聚类簇以获得最终的聚类结果。
DBSCAN,全名为 D e n s i t y − B a s e d Density-Based Density−Based S p a t i a l Spatial Spatial C l u s t e r i n g Clustering Clustering o f of of A p p l i c a t i o n Application Application w i t h with with N o i s e Noise Noise,即基于密度对噪声鲁棒的空间聚类 ( ( (一知乎前辈是这样翻译的,我觉得还挺准确的 ) ) ),是一种典型的基于密度的聚类算法。本篇博客就介绍介绍它─=≡Σ(((つ•̀ω•́)つ。
1. 基本概念
DBSCAN算法根据邻域参数 ϵ \epsilon ϵ和 M i n P t s MinPts MinPts来刻画样本分布的紧密程度。假设有数据集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1,x2,...,xm}:
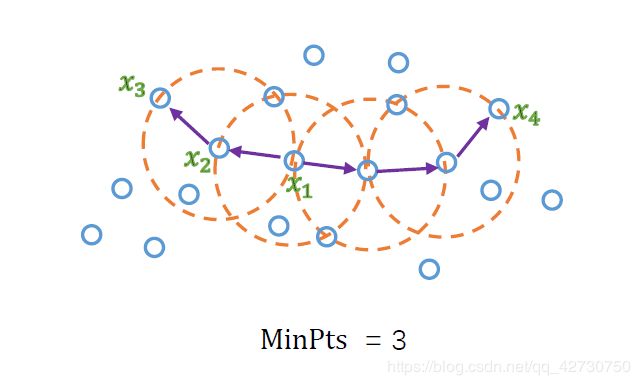
- ϵ \epsilon ϵ-邻域 ( ϵ − n e i g h b o r h o o d ) (\epsilon-neighborhood) (ϵ−neighborhood):对 x j ∈ D x_j \in D xj∈D,其 ϵ \epsilon ϵ-邻域包含样本集 D D D中与 x j x_j xj的距离不大于 ϵ ( \epsilon( ϵ(半径 ) ) )的样本,即 N ϵ ( x j ) = { x i ∈ D ∣ d i s t a n c e ( x i , x j ) ≤ ϵ } N_{\epsilon}(x_j)=\{x_i \in D|distance(x_i,x_j)\leq\epsilon\} Nϵ(xj)={xi∈D∣distance(xi,xj)≤ϵ}。如上图中,半径 ( ϵ ) (\epsilon) (ϵ)就是紫色的箭头, ϵ \epsilon ϵ-邻域就是橙色圆所在区域。
- 核 心 对 象 核心对象 核心对象 ( c o r e (core (core o b j e c t ) object) object):若 x j x_j xj的 ϵ \epsilon ϵ-邻域至少包含 M i n P t s MinPts MinPts个样本,即 ∣ N ϵ ( x j ) ∣ ≥ M i n P t s |N_{\epsilon}(x_j)|\geq MinPts ∣Nϵ(xj)∣≥MinPts,则 x j x_j xj是一个核心对象。如上图中的 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4。
- 密 度 直 达 密度直达 密度直达 ( d i r e c t l y (directly (directly d e n s i t y − r e a c h a b l e ) density-reachable) density−reachable):若 x j x_j xj位于 x i x_i xi的 ϵ \epsilon ϵ-邻域中,且 x i x_i xi是核心对象,则称 x j x_j xj由 x i x_i xi密度直达。如上图中的 x 2 x_2 x2由 x 1 x_1 x1密度直达, x 3 x_3 x3由 x 2 x_2 x2密度直达。
- 密 度 可 达 密度可达 密度可达 ( d e n s i t y − r e a c h a b l e ) (density-reachable) (density−reachable):对 x i x_i xi与 x j x_j xj,若存在样本序列 p 1 , p 2 , . . . , p n p_1,p_2,...,p_n p1,p2,...,pn,其中 p 1 = x i p_1=x_i p1=xi, p n = x j p_n=x_j pn=xj且 p i + 1 p_{i+1} pi+1由 p i p_i pi密度直达,则称 x j x_j xj由 x i x_i xi密度可达。如上图中, x 3 x_3 x3由 x 1 x_1 x1密度可达, x 4 x_4 x4由 x 1 x_1 x1密度可达。
- 密 度 相 连 密度相连 密度相连 ( d e n s i t y − c o n n e c t e d ) (density-connected) (density−connected):对 x i x_i xi与 x j x_j xj,若存在 x k x_k xk使得 x i x_i xi与 x j x_j xj均由 x k x_k xk密度可达,则称 x i x_i xi与 x j x_j xj密度相连。如上图中, x 3 x_3 x3与 x 4 x_4 x4密度相连。
- 簇 簇 簇 ( c l u s t e r ) (cluster) (cluster):由密度可达关系导出的最大的密度相连样本集合 C C C。
- 边 界 点 边界点 边界点 ( b o r d e r (border (border p o i n t ) point) point):位于核心点的邻域内,但自身领域内样本点个数小于 M i n P t s MinPts MinPts的样本;
- 噪 声 噪声 噪声 ( n o i s e ) (noise) (noise):数据集 D D D中不属于任何簇的样本。
2. 算法流程
对于给定的邻域参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts):
- 计算各个样本点之间的距离;
- 找出各样本的 ϵ \epsilon ϵ-邻域并确定核心对象集合 Ω \Omega Ω;
- 从 Ω \Omega Ω中随机选取一个核心对象作为种子,找出由它密度可达的所有样本,即构成了第一个聚类簇 C 1 C_1 C1;
- 将 C 1 C_1 C1中包含的核心对象从 Ω \Omega Ω中去除,更新 Ω \Omega Ω;
- 从更新后的集合 Ω \Omega Ω中随机选取一个核心对象作为种子来生成下一个聚类簇 C 2 C_2 C2;
- 不断重复上述过程,直至集合 Ω \Omega Ω为空,得到最终的聚类结果 C = { C 1 , C 2 , . . . , C n } C=\{C_1, C_2,...,C_n\} C={C1,C2,...,Cn}。
3. 代码实现
根据上述算法流程,我用递归的方法实现了该算法。数据加载函数和画图函数可以参考以前的博客,主要代码如下:
import matplotlib.pyplot as plt
import numpy as np
def o_distance(data):
"""
计算样本点之间的距离(欧式距离的平方)
:param data:
:return:
"""
dim_m = np.shape(data)[0]
distance = np.array(np.zeros(shape=(dim_m, dim_m)))
for index in range(dim_m):
temp = data[index] - data
distance[index] = np.sum(np.square(temp), axis=1)
return distance
def get_coreobject(distance, r, minpts):
"""
找出各样本的邻域并确定核心对象集合
:distance:
:r:
:minpts:
:return: 各样本的索引
"""
coreobject = []
neighborhood = []
dim_m = np.shape(distance)[0]
for index in range(dim_m):
if len(distance[index][distance[index] <= r]) - 1 >= minpts:
coreobject.append(index)
# 返回元组
y = np.where(distance[index] <= r)[0]
neighborhood.append(np.setdiff1d(y, [index]))
return np.asarray(coreobject), np.asarray(neighborhood)
def get_cluster(coreobject, neighborhood, coreobject_random):
core_o.append(coreobject_random)
coreobject_index = np.where(coreobject == coreobject_random)[0][0]
core_index.append(coreobject_index)
# 核心对象的邻域
for ddr in neighborhood[coreobject_index]:
# 密度直达, 即邻域里的样本
if ddr not in C1:
C1.append(ddr)
if ddr in coreobject:
# 如果这个样本也是核心对象, 继续找它的密度直达
get_cluster(coreobject, neighborhood, ddr)
else:
for border_point_index in range(len(neighborhood)):
if ddr in neighborhood[border_point_index]:
# 这是一个边界点, 然后找其核心对象
border_point_core = coreobject[border_point_index]
if border_point_core in coreobject:
get_cluster(coreobject, neighborhood, border_point_core)
else:
continue
def dbscan(coreobject, neighborhood):
"""
DBSCAN算法实现---递归---简单粗暴
:param coreobject: 核心对象集合
:param neighborhood: 核心对象的邻域集合
:return: 返回的簇不包含未标记的样本点
"""
# 总簇
C = []
global C1
global core_o
global core_index
while len(coreobject) > 0:
C1 = []
core_o = []
core_index = []
# 随机选择核心对象
coreobject_random = np.random.choice(coreobject)
C1.append(coreobject_random)
get_cluster(coreobject, neighborhood, coreobject_random)
C.append(C1)
coreobject = np.setdiff1d(coreobject, core_o)
neighborhood = np.delete(neighborhood, obj=core_index)
return C
def get_label(data_arr, cluster_c):
dim_m = np.shape(data_arr)[0]
labels = np.array(-np.ones(shape=dim_m, dtype=np.int8))
label_num = 0
for index in cluster_c:
labels[index] = label_num
label_num += 1
return labels
if __name__ == '__main__':
data_arr = load_data('./data/data.txt')
distance_arr = o_distance(data_arr)
coreobject, neighborhood = get_coreobject(distance_arr, 0.07, 7)
cluster_c = dbscan(coreobject, neighborhood)
labels = get_label(data_arr, cluster_c)
draw_picture(data_arr, labels)
DBSCAN算法主要在于参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts)的选择,需要不断的去尝试,这也是它的不足之处吧。上图的参数是 ( 0.07 , 7 ) (0.07,7) (0.07,7),如果改成 ( 0.05 , 7 ) (0.05,7) (0.05,7),就变成了下面这个结果,图中的黑点被划分为了噪声。
结束语
这篇博客终于写完了哈哈哈,快一个周了─=≡Σ(((つ•̀ω•́)つ,白天复习晚上抽一点时间写写博客,敲敲代码。我的DBSCAN实现代码相比其他的代码思路稍微清晰些,简单粗暴地用递归实现了哈哈哈哈(~ ̄▽ ̄)~ ,毕竟如果用递归处理大样本数据开销还是稍微有点大的,除此之外,里面还有几处需要优化的地方,比如那个找边界点的地方。以后有想法再优化哈哈哈哈,睡觉(⁎˃ᴗ˂⁎)。