入坑Algorithms - 算法图解（上）

正如作者所说这是一本像小说一样有趣的算法入门书。本书作者使用通俗易懂的语言，再加上形象生动的小例子，通过简单的图像形式让你更快的理解内在的原理。这种书才适合作为专业入门，科普知识的经典教科书。本书会有一些代码，代码是基于Python语言编写的。

目录

第一章 算法简介

第二章 选择排序

第三章 递归

第四章 快速排序

第五章 散列表

第六章 广度优先搜索

第七章 狄克斯特拉算法

第八章 贪婪算法

第九章 动态规划

第十章 K最近邻算法

第十一章 接下来学习的内容

 

第一章 ：

本章用二分查找引入算法的概念，通过二分查找与简单查找方式的对比来引入算法的性能：时间复杂度和空间复杂度（文中主要用大O表示法来介绍时间复杂度）。

五种常用的大O运行时间如下：

1. O（log（n））：对数时间
2. O（n）：线性时间
3. O（n*log（n））：速度较快的算法
4. O（n的平方）：速度较慢的算法（选择排序）
5. O（n！）：非常慢的算法（比如旅行商问题的解决方案）

时间复杂度的理解：

• 算法的速度指的并非时间，而是操作数的增速。
• 谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。

二分查找只有在所查找的内容有一定的顺序关系时才能使用。二分查找的具体代码如下：

 

#二分查找算法实现代码

def binary_search(list,item):
    '''
    :param list: 要查找的数据组
    :param item: 要在数据组中查找的某个数据
    :return: item的当前索引位置
    '''
    low = 0
    high = len(list)-1
    while low <= high:
        mid = ((low + high) // 2)+1
        guess = list[mid]
        if guess == item:
            return mid
        elif guess > mid:
            high = mid - 1
        else:
            low = mid + 1
    return None


my_list = [1,3,5,7,9,11,13,15,17,19]

print(binary_search(my_list,5))

运行结果：2

 

本章有趣的例子：查找电话本，白纸上画网格，旅行商等

 

第二章：

本章先是通过讲解内存的工作原理来引入两种常用的数据结构：数组和链表；通过数组和链表的索引、插入和删除来对比讨论选择排序在两种数据结构上的优缺点。

数组和链表：

• 如果将一组数据存在数组中，需要连续的足够的物理空间来存储；一旦数据需要增加而相邻位置没有了空间，就得将数据迁移到更大的空间上去。
• 如果将一组数据存在链表中，物理空间可以是足够但不一定连续的，链表的物理空间不仅存储了数据而且存储了下一个物理空间的位置，实现了逻辑上的连续。如果需要增加数据，只需要将增加的数据的位置在已有的数据中表现出来即可。
• 数组的元素带编号，编号是从0而不是1开始的，元素的位置称为索引。

中间插入和删除：

• 链表中间插入和删除比较简单，只需要改变物理空间的地址。
• 数组的中间插入需要将后面的一半数据平行往后移动；数组在删除后的空间也需要通过移动数据来填充。

查找：

• 数组的数据具有所有编号很方便读取各个位置的数据
• 链表则需要对整个链表遍历进行数据的读取

选择排序：

• 选择排序是对长度为K的数据进行K次循环遍历，每次找到一个符合当前要求的数据，K次后完成排序。
• 选择排序的时间复杂度为O（n的平方），请思考为什么不是O（n!）？？？

选择排序代码如下：

 

#选择排序代码实现

def findSmallest(arr):
    '''
    :param arr: 一组数据
    :return: 最小数据的索引位置
    '''
    smallest = arr[0]
    smallest_index = 0
    for i in range(1,len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

def selectionSort(arr):
    '''
    :param arr: 一组数据
    :return: 从小到大排好顺序的数据
    '''
    newArr = []
    for i in range(len(arr)):
        smallest_index = findSmallest(arr)
        newArr.append(arr.pop(smallest_index))       #此处的pop方法是列表的一种方法
    return newArr

arr = [5,3,2,6,10]
print(selectionSort(arr))

运行结果：[2, 3, 5, 6, 10]

 

本章将计算机的内存形象的比作一大堆抽屉，每一个内存空间就像一个个的抽屉。

 

第三章：

本章主要介绍递归的编程方法，并且引入了另一种数据结构：栈。

递归：是实现自我调用的一种编程方法。

两个条件：

• 基准条件：函数自我调用的结束条件，避免函数进入死循环。
• 递归条件：函数调用自已

栈：是一种类似于顶部开口的箱子，比如我们想把叠好的衣服放入箱子中；只能从上面依次放入和拿出。

栈的两个操作：

• 压入
• 弹出（后进先出）

调用栈：计算机在内部使用被称为调用栈的栈。计算机将为每个调用栈分配一个内存块，程序的运行就是调用每个含有函数的内存块，而且将每个内存块按调用的先后顺序存放在栈中。

递归调用栈：递归调用栈和调用栈的原理是相同的，只是递归调用时只对函数中的变量进行了修改，作为一个新的内存块放入到栈中，实现调用的过程。

调用栈可能很长，这将占用大量的内存。

扩展内容：高级递归主题：尾递归

 

第四章：

本章通过农场主划地的例子引入分而治之（D&C）的思想，快速排序正是使用了这种分而治之的策略。

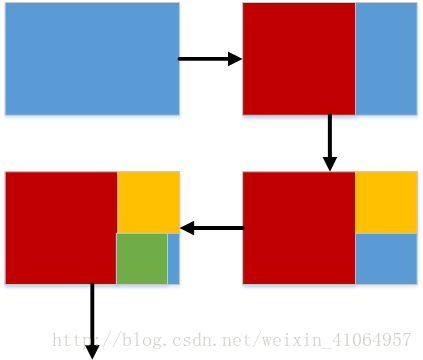
例子1：农场主划地

假设有一个农场主，他有一块地。他想将这块地均匀的分成方块，且使分出的方块尽可能大。

如图所示一直分下去；如果剩余形状的长是宽的整数倍，则为分割的基准条件，即完成分割，方块的边长为剩余形状的宽，且为可分的最大方块。

如果不能理解分出的方块即为可分得的最大方块：可参见欧几里得算法的思想（最大公约数算法）；即蓝色土地块可分得的最大方块和去掉红色方块后的蓝色部分可分得的最大方块是一样的，且为两者的最大公约数。

例子2：一组数据求和

一组数据的求和同样是采用分而治之的思想，代码如下：

 

#sum函数的代码

def sum(arr):
    '''
    :param arr: 一个列表
    :return: 列表所有元素的和
    '''
    if arr == []:
        return 0
    return arr[0] + sum(arr[1:])

list = [1,3,5,7,9]
print(sum(list))

运行结果：25

 

 

例子3：递归实现列表含有的元素数，代码如下：

 

#递归实现列表中包含元素的个数

def count(arr):
    if len(arr) == 0:
        return 0
    return 1 + len(arr[1:])

list = [1,1,2,2,3,4,3,4,5,6,2]
print(count(list))

运行结果：11

 

例子4：递归实现列表中最大数，代码如下：

 

#求列表中的最大数

def max(arr):
    if len(arr) == 2:
        return arr[0] if arr[0] > arr[1] else arr[1]
    sub_max = max(arr[1:])
    return arr[0] if arr[0] > sub_max else sub_max

list = [3,1,5,2,6,2,83,98,235,1,4,2,6,2]
print(max(list))

运行结果：235

 

快速排序：

两个步骤：挑选基准值（基准值的选择对运行效率的影响很大）和对数据进行分区

三个组成部分：所有小于基准值数字组成的子数组、基准值、所有大于基准值数字组成的子数组

 

#快速排序的算法递归实现

def quicksort(arr):
    if len(arr) < 2:
        return arr
    else:
        pivot = arr[0]
        less = [i for i in arr[1:] if i < pivot]
        bigger = [i for i in arr[1:] if i > pivot]
        return quicksort(less)+[pivot]+quicksort(bigger)

list = [6,2,8,4,3,1,7,5]
print(quicksort(list))

运行结果：[1, 2, 3, 4, 5, 6, 7, 8]

 

归并排序：

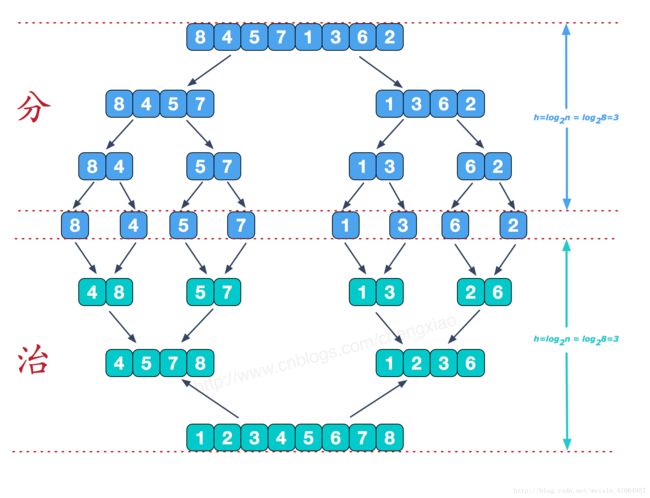
分而治之的总体思想过程：

归并排序的三个层次：

 

1. 初始时，把待排序序列中的n个记录看成n个有序子序列，每个子序列的长度均为1，所以每个子序列都是有序的。
2. 把当时序列组里的有序子序两归并，完成一遍后序列组里的排序序列个数减半，每个子序列的长度加倍。
3. 对加长的有序子序列重复上面的操作，最终得到一个长度为n的有序序列。

具体实现代码如下：

 

 

#归并排序

def merge(left,right):
    '''
    最划分好的数组单元进行一一的归并排序
    :param left: 有序序列的左部分
    :param right: 有序序列的右部分
    :return: 新的排序序列
    '''
    new_list = []
    j = k = 0
    while j < len(left) and k < len(right):
        if left[j] < right[k]:
            new_list.append(left[j])
            j += 1
        else:
            new_list.append(right[k])
            k += 1

    if j == len(left):
        for i in right[k:]:
            new_list.append(i)
    else:
            for i in left[j:]:
                new_list.append(i)

    return new_list


def mergesort(lists):
    '''
    将数组进行划分知道划分到最小的数组单元（仅含一个元素）
    :param lists:一组数据
    :return: 返回对参数进行过排序的数据
    '''
    if len(lists) < 2:
        return lists
    middle = len(lists)//2
    left = mergesort(lists[:middle])
    right = mergesort(lists[middle:])
    return merge(left,right)

#如果执行运行则执行if语句的内容，若作为模块导入使用则不运行if语句的内容。
if __name__ == '__main__':
    list = [4, 7, 8, 3, 5, 9]
    print(mergesort(list))

运行结果：[3, 4, 5, 7, 8, 9]

 

本章另外对大O表示法进行了更深入的讲解，分别从最优情况、平均情况、最糟情况三个方面给出图解。并且通过归并排序和选择排序的比较，来讨论排序算法的时间复杂度。