tony问题

 

Tony问题的解决

注：本文来自CSDN论坛，这是一次有关透视的应用的热烈讨论。透视是射影几何的基本知识，不学过射影几何就不知道它，就会把它与仿射甚至相似混起来。这次讨论参加的人数有15人之多，只有3-4个人真正了解透视，足见学点射影几何的必要。

本文原不清插图部分已重画，明显无关贴已删除，其余问题待整理。

主　　题：  数学问题

提  问  者： tony1978 (突击召唤师) 

等　　级：   

信 誉 值： 100

所属论坛： 专题开发 数据结构与算法

问题点数： 100

回复次数： 80

发表时间： 2002-07-19 11:15:18Z

本论坛参与者 ：除提问作者tony外，还有14人，如下：

 WGJ0122, xdspower, eion(那个谁) ,ccat(智拙) ,

quicmous(快鼠) ,zhenming_liu(), java_skater(skater), 

jojoship(天天聊天) , zzwu(未名) , LeeMaRS(小菜虎，仍需努力) ,

xf8zbf(瞎想) ,dearmite(笨笨的我*_^),  xqr(星球人) , 

hanqiong1(瀚琼)

___________________________________________________________________________________________________________

 

问题：

   计算机屏幕四个顶点(0,0) (1024,0) (0,768), (1024,768)

投影到幕布上的坐标是(a1,b1) (a2,b2) (a3,b3)(a4,b4) 均为

已知，求幕布上任意一点(x,y)在屏幕上的坐标。

 

提示：

   屏幕是一个标准矩形，以左上角为(0,0)。投影可能是一个

倾斜的四边形，以幕布的左上角为(0,0)。

________________________________________________________________________________________________________

  

 

 1。回复人： wgj0122() ( ) 信誉：98  2002-07-19 12:14:10Z  得分:0 

相似形的问题。

过点（X，Y）垂直屏幕沿x轴和y轴作两个平面。剩下的用初中相似形知识就行了。 

Top

 

 2。回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-19 13:00:40Z  得分:0

要是下面这样的形状呢？

这是很容易出现的，这时候怎么用相似啊？

 

Top 

 3。回复人： wgj0122() ( ) 信誉：98  2002-07-19 13:14:56Z  得分:0 

你的问题中幕布和屏幕的边是不是平行的呀？ 

 

Top 

 4。回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-19 14:13:07Z  得分:0 

用投影仪投在幕布上，实际使用中，投影仪不大可能完全投影出一个矩形。一般是梯形（投影仪光束向上下或左右倾斜），或者不规则的四边形（比如说从左下向右上投影）

 

Top 

 5. 回复人： xdspower() ( ) 信誉：130  2002-07-19 15:34:58Z  得分:0 

其实这个问题是要转换为求两个平面的夹角，再计算一个平面到另一个平面投影 

 

Top 

 6. 回复人： eion(那个谁) ( ) 信誉：100  2002-07-19 16:27:10Z  得分:5 

假定屏幕和幕布都是平面——没有弯曲

 

由于屏幕是光源，所以幕布上影子的大小肯定比屏幕大，

我们可以将屏幕看作是幕布在屏幕所在平面上的投影，

又：三点确定一个平面，所以只需要三个点就OK了，

设对应的顶点为

A : (0,    0  )- (a1, b1) A'

B : (1024, 0  ) - (a2, b2) B'

C : (0,    768) - (a3, b3) C'

D : (1024, 768) - (a4, b4) D'

我们只考虑A,B,C和A',B',C'

 

设屏幕坐标为(x,y)投影导幕布坐标(x',y')，设坐标变换方程为：

x = a*x' + b*y' + c   (1)

y = d*x' + e*y' + f   (2)

 

(注：平面到平面的变换是线性变换，而由(x',y')到(x,y)变换的一般形式就是上面的形式)

将A,B,C 的坐标代入，(1),(2)共由6个方程，6个未知数a,b,c,d,e,f

A,B,C代入第一个方程

0   = a*a1 + b*b1 + c   (3)

1024 = a*a2 + b*b2 + c   (4)

0   = a*a3 + b*b3 + c   (5)

 

(4)-(3)===> 1024 = a*(a2-a1) +b*(b2-b1);    (6)

(4)-(5)===> 1024 = a*(a2-a3) +b*(b2-b3);    (7)

 

(6)*(a2-a3)-(7)*(a2-a1) ==>

1024*(a2-a3)-1024*(a2-a1) =b*(b2-b1)*(a2-a3) - b*(b2-b3)*(a2-a1)

 

所以： b = ??????/??????

代入 (6)，求得 a=????/????

代入 (3)，求得 c=????/????

 

同理，求得 e,f,g. 

 

Top 

 7. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-19 18:30:39Z  得分:0 

感谢[eion(那个谁)]，我会给分的！不过还是有个问题，因为投影仪可能是倾斜的（这个样/或者\）。这时候可以认为屏幕和投影不在同一个坐标系中，两个坐标系是有夹角的。问题的难度大多了。之所以给了四个点，就是因为这个原因。我看到别人的程序要求9个点（屏幕上的一个田字格），因为得不到源码，不知道是怎么算的。 

 

Top 

 8. 回复人： ccat(智拙) ( ) 信誉：100  2002-07-19 19:26:08Z  得分:0 

空间三点可以决定一个平面，四点应当可以了吧，让我想想 

 

Top 

 9. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-19 23:24:07Z  得分:20  

to tony1978(突击召唤师) :

你的问题是射影几何问题，应该采用仿射变换和射影变换的复合变换求解。 eion(那个谁)的解法只考虑了仿射变换，因此无法解决你的疑问。如不清楚我们可继续讨论。 

 

Top 

10. 回复人： zhenming_liu() ( ) 信誉：99  2002-07-20 21:26:14Z  得分:0  

如果坐标系交角是斜的，那可以用linear algebra中坐标系变换的知识，乘以一个matrix就行了，但是这里还有个拉伸的过程，一定需要九个点，譬如，在透影中，以左边和下把边确定的coordinate system和以右边，上边确定的coordinate system所决定的原点的位置是有所不同的，9个点大概是用来判断单位长度随位置的变化的变化的。 

 

Top 

 11. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-20 22:00:25Z  得分:0  

to zhenming_liu() :你说的就是射影几何的射影变换，把n+1维空间的图形投影到n维空间的变换。特点是，直线的投影仍然是直线；一束平行线可能投影成一束共点的直线(类似我们看到平行的铁轨相交于无远点）.. 

 

Top 

 12. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-21 16:25:19Z  得分:0  

呵呵，今晚上我给出完整的答案... 

 

Top 

 13. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-21 18:32:08Z  得分:0 

 

一、一般情况 

   设液晶屏坐标为P(x,y,z),银幕射影坐标（请参见射影几何的教材）为P'(x',y',z')，射影变换为：

 

   x' = a11*x + a12*y + a13*z + a14

   y' = a21*x + a22*y + a23*z + a24

   z' = a31*x + a32*y + a33*z + a34

 

   确定该变换需要确定12个系数a[i,j],因此至少需要4对原点和像点。

 

   注，由于点A(x',y',z')和B(x'/z',y'/z',1)在射影平面 z'=1 上，对应同样的像.因此上面的坐标变换实际上包含了两个基本变换：

   (1)液晶屏坐标P(x,y,z)映射到p'(x',y',z')，这里z=0

   (2)P'(x',y',z')投影到平面z'=1上，坐标为(x'/z',y'/z',1)，其中(x'/z',y'/z')是银幕坐标;

 

二、本问题解法

 

假设液晶屏上的原点坐标为(x1,y1,z2),(x2,y2,z2),...;

银幕上的映像坐标为(x1',y1',z1'),(x2',y2',z2'),...;

则有：

   (x1,y1,z1)=(0,0,0)

   (x2,y2,z2)=(1024,0,0)

   (x3,y3,z3)=(0,768,0)

   (x4,y4,z4)=(1024,768,0)

   

   x1'/z1' = a1

   y1'/z1' = b1

   x2'/z2' = a2

    y2'/z2' = b2

   x3'/z3' = a3

   y3'/z3' = b3

   x4'/z4' = a4

   y4'/z4' = b4

 

   把上述条件带入坐标变换公式即可利用线性方程组解法求出12个系数. 

 

Top 

 14. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-22 08:29:32Z  得分:0  

还是不明白，旋转怎么办啊？(1024,768)这样的坐标是按照屏幕坐标系，可是屏幕坐标系和银幕是有夹角的啊，是x/y方向的夹角，怎么办？

 

 

Top

 

 15. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-22 08:50:12Z  得分:0 

 

换个角度考虑呢？比如我知道9个点，那么，同一条线上的三个点，(0,0),(512,0),(1024,0)他们的投影(a1,b1),(a2,b2),(a3,b3)已知，一维考虑，可以求得这条投影线上任意一点的源坐标(x,y)。9个点构成一个田字格，投影可能是这样的：

 

 .  *    `

 .  .     .

*  .

           *

 

二维变换，我不太懂了。 

 

Top 

 16. 回复人： eion(那个谁) ( ) 信誉：100  2002-07-22 09:03:15Z  得分:20 

 

只要是平面，三个点就决定了，所以多余3个点的都是多余。

 

但是由于一般的屏幕并非都是纯平面，所以需要近似。这时你可以采用

最小二乘法来求得最贴近的平面变换。否则，象你所说的，为什么有的

人要用9个点来计算？无非是为了减少误差

 

想想，一个平面在另外一个平面上的投影，除了平行是跟原来是一样的

外，其他的，只有坐标的旋转和延伸，坐标的旋转，根据坐标旋转公式

我们知道是一个线性变换，而延伸也是线性变换，所以最后还是线性变

换，正因为是线性变换，所以只需要4个参数（2^2），又因为对原点有

偏移，所以还要加上2个原点坐标

[ x ]  [ a   b ]  [ x' ]   [ c ]

|  | = |       |* |    |  +|   |

[ y ]  [ d   e ]  [ y' ]   [ f ]

       ----+---

            |

            +----这个矩阵表示了两个平面坐标系的变换，

                 如果是正交矩阵，那么就是旋转变换，

                 否则，可以是任意的线性变换，2*2

 

简单一点,如果是一条线投影到另外一条线上，只需要两个点

设原来的点坐标为 x0,x1 投影后坐标为 y0,y1且

|x1-x0| = |y1-y0|

不一定成立，所以坐标变换应该是

x =  a  *x' + b

    -+-

     |

     +-----  一维的为 1*1矩阵

 

正好两个点，两个未知数，可求出 a,b

 

 

 

Top

 

 17. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-22 15:10:43Z  得分:0 

 

看个图http://user.7host.com/oneday/img.gif

投影还是有一点特别

 

Top 

 18. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-22 15:51:30Z  得分:0  

一、一般情况

   我分析了一下我给出的方程，一般情况下估计需要知道6个点才能确定变换的方程。

二、矩形区域

   另外有一个纯几何的方法，问题求解的充分必要条件是在知道“矩形”4个顶点的前提下就足以完成题目。原理如下：

   射影变换保持直线的不变性，即直线的射影仍然是直线。因此，液晶屏幕的中心是液晶屏对角线的交点，其射影必然是投影四边形对角线的交点。

   因此，原则上可以借助于二分法确定像平面与原像平面上点的对应关系。 

 

Top 

 19. 回复人： java_skater(skater) ( ) 信誉：100  2002-07-23 05:44:10Z  得分:0  

大概的想法：

 

     因为不管是屏幕还是幕布都是成比例显示的，所以：

 

     (nx,ny)是屏幕上的坐标。(x,y)是幕布上的坐标。

     

     nx=1024*x/(a4-a1)

 

     ny=768*y/(b4-b1)

 

你参考一下吧，也许对你会有帮助！ 

 

Top 

 20. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-23 08:45:19Z  得分:0 

如果像楼上说得那么简单，就不用算了。似乎计算机图形学中有讲到，但是三四年没看了，现在想来很吃力，呵呵。是投影变换

 

Top 

 21. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 13:55:54Z  得分:0 

 

to： tony1978(突击召唤师)

我给出的变换包含两个基本变换：

第一步：把位于xy平面上的屏幕坐标经过仿射变换转换到三维坐标系。这个变换本身包含平移、旋转等几何变换。

第二步：以三维坐标原点为光源的投影变换，投影平面是z=1,公式如下P(x,y,z)->p'(x',y',z')

   x'= x/z

   y'= y/z

如果给出的已知点没有特殊性的话，可能需要6个才能确定变换方程。

 

对于本问题，已知矩形的四个顶点的投影坐标足够了（是充分必要条件）。几何解法如下：

1.液晶屏四个顶点是A,B,C,D,对应的投影是A',B',C',D'.

任给一点P,如果P是AC,BD的交点，则P'是A'C',B'D'的交点。

2.如果P并非AC,BD的交点，

假设ABCD的中心为Q则过Q做AB,AD的平行线m,n，把ABCD分成四个小矩形。P点必定落在其中之一。

同样，过Q的投影Q'做A'B',A'D'的“平行线”（并不一定平行，参见后面的说明）m',n'把A'B'C'D'分成四个部分,P'必然落在和P相对应的四边形区域。

3.关于平行线的投影：

一组平行线投影到一个平面上，有两种可能性：（1）继续保持平行（包括重合）；（2）投影成一组相交的直线。

对于本文题，如果A'B'和C'D'相交于T'，则m'必然经过T'

上述过程迭代下去，可逐步求出P'的坐标。

到此为止，从理论上给出了解法。 

 

Top 

 22. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 13:57:17Z  得分:0  

to： tony1978(突击召唤师)

我给出的变换包含两个基本变换：

第一步：把位于xy平面上的屏幕坐标经过仿射变换转换到三维坐标系。这个变换本身包含平移、旋转等几何变换。

第二步：以三维坐标原点为光源的投影变换，投影平面是z=1,公式如下P(x,y,z)->p'(x',y',z')

   x'= x/z

   y'= y/z

如果给出的已知点没有特殊性的话，可能需要6个才能确定变换方程。

 

对于本问题，已知矩形的四个顶点的投影坐标足够了（是充分必要条件）。几何解法如下：

1.液晶屏四个顶点是A,B,C,D,对应的投影是A',B',C',D'.

任给一点P,如果P是AC,BD的交点，则P'是A'C',B'D'的交点。

2.如果P并非AC,BD的交点，

假设ABCD的中心为Q则过Q做AB,AD的平行线m,n，把ABCD分成四个小矩形。P点必定落在其中之一。

同样，过Q的投影Q'做A'B',A'D'的“平行线”（并不一定平行，参见后面的说明）m',n'把A'B'C'D'分成四个部分,P'必然落在和P相对应的四边形区域。

3.关于平行线的投影：

一组平行线投影到一个平面上，有两种可能性：（1）继续保持平行（包括重合）；（2）投影成一组相交的直线。

对于本文题，如果A'B'和C'D'相交于T'，则m'必然经过T'

上述过程迭代下去，可逐步求出P'的坐标。

到此为止，从理论上给出了解法。 

 

Top 

 23. 回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 18:41:10Z  得分:0  

这个题目应该是点光源投影，否则若是平行光投影就太简单了，或是不规则光投影就无法可解.

我有了精确的计算机求解此题的方法，有需要的朋友给我发信讨论吧，

我的信箱是：[email protected] 

 

Top 

 24. 回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 18:45:14Z  得分:5 

 

还是再说明一下吧，点光源投影的话，四边形的可能性很多，也许投影的形状就是一条线段，但多半都是不规则形状，用比例的办法是无法解答的，而且，此题最好用计算机求解，要用到递归的思想，还是和我讨论一下吧，我也想得到最好的解决方法。 

 

Top 

 25. 回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 18:50:17Z  得分:0 

还有，我以为这题无法完全用立体几何的知识解答，quicmous(快鼠) 的思想和我差不多，但他不是考虑的点光源投影，平行光投影用比例的方法解决就完全可以，但点光源不行

 

Top 

 26. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 19:41:01Z  得分:0 

关于点光源投影：

   我在楼上的帖子已经说得很清楚了。如果原像是矩形（或平行四边形），在得到像的四个顶点坐标后就可以确定任意一个原像点的投影坐标（反之亦然）。原因如下：如果我们在液晶屏上画上坐标网格线，如果像是个斜四边形，则水平的网格线将全部交于同一点，竖直网格线全部交于另外一点。

   这方面参考资料可以参阅：射影几何学、画法几何学、测量学、建筑设计、美术（透视学）等。 

 

Top 

27.  回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 19:57:05Z  得分:0 

但是，你是在解决数学问题还是在解决计算机解题的问题呢？

立体坐标的建立就是个迷！

当然，如果有了立体坐标，还用做吗？

A1X+B1Y+C1Z=D1

A2X+B2Y+C2Z=D1

A3X+B3Y+C3Z=D1

这个方程组用线性代数一下下就搞定了呀！

分割的思想我们都有想到，还是来信讨论吧 

 

Top 

 28. 回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 19:58:44Z  得分:0 

坐标变换是个有趣的思想啊 

 

Top 

 29. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 20:03:12Z  得分:0 

给出一个仿射坐标系的解法：

我们以投影四边形的两个相邻的边A'B'和A'D'为轴建立仿射坐标系，可以给出一个解法，至于如何把仿射坐标变换成直角坐标本帖子不予考虑。

原像点A(0,0),B(w,0),C(w,h),D(0,h);(注：显示器的直角坐标）

像点A'(0,0),B'(w',0),C'(w'',h''),D'(0,h')，则有如下射影关系:

A(0,0,0)->A'(0,0,1)

B(w,0,0)->B'(w',0,1)

D(0,h,0)->D'(0,h',1)

C(w,h,0)->C'(w'',h'',1)

由于射影变换为:

x'=(a11*x+a12*y+a13*z+a14)/(a31*x+a32*y+a33*z+a34)

y'=(a21*x+a22*y+a23*z+a24)/(a31*x+a32*y+a33*z+a34)

不妨假设a34=1(因为可能有无数种等价的解,我们只选择其中之一)

故

a14=0

a24=0

w*a11/(w*a31+1)=w'

a21=0

a12=0

a22*h/(h*a32+1)=h'

w*a11/(w*a31+h*a32+1)=w''

h*a22/(w*a31+h*a32+1)=h''

 

这时:a14=0,a24=0,a21=0,a12=0.对于a11,a22,a31,a32可以通过下面线性方程组求解:

( w   0    -w'w       0 ) (a11)   ( w' )

( 0   h      0        h'h) (a22) = ( h' )

( w   0      -w''w  -w''h) (a31)  ( w'')

( 0   h      -h''w  -h''h) (a41)  ( h'')

 

嗬嗬,我不解了.但已经说明四个点足以确定点光源的射影变换. 

 

Top 

30.  回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 20:08:30Z  得分:0 

平行线的点光源投影并不一定平行，多半有可能投影后会相交的，如果平行的话就好做多了嘛！

点光源S和直线AB、CD确定两个平面，其中AB平行于CD，加上投影面OPQ就是三个平面，SAB与SCD相交于MN，如果MN平行于OPQ，则AB、CD的投影A1B1、C1D1两两平行；如果MN交OPQ于P，则A1B1、C1D1相交于P。这是三个平面相交，交线不平行则交于一点的“美丽”。 

 

Top 

 31. 回复人： jojoship(天天聊天) ( ) 信誉：100  2002-07-23 20:19:18Z  得分:0 

好可爱的坐标变换啊！基础是建立在原平面与投影平面平行基础上的吗？那的确是对的。可是，不平行呢！？ 

 

Top 

 32.  回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 21:02:42Z  得分:0 

对于任意四边形，原像四边形也采用仿射坐标，解法和上面差不多。

 

Top 

 33. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-23 21:31:37Z  得分:0  

to jojoship(天天聊天):

你根据影射：

A(0,0,0)->A'(0,0,1)

B(w,0,0)->B'(w',0,1)

D(0,h,0)->D'(0,h',1)

C(w,h,0)->C'(w'',h'',1)

断定原像平面和像平面平行，其实是误解，因为原像到像的变换是一个线性变换和摄影变换构成的复合变换。首先原像经过一个线性变换得到位置可能很“别扭”的中间像，中间像再投影到z=1平面上。正如你能看到的，我在楼上帖子里的方程式是非线性的（射影变换）。 

 

Top 

 34. 回复人： zzwu(未名) ( ) 信誉：106  2002-07-24 08:16:58Z  得分:0   

1.我同意quicmous前面回复14,21提到的二分或四分法来解决。定位速度实际极快.下面我具体落实一下怎样实际来做这一工作,不再讨论理论根据,有错大家指出。 

2.四分概念:

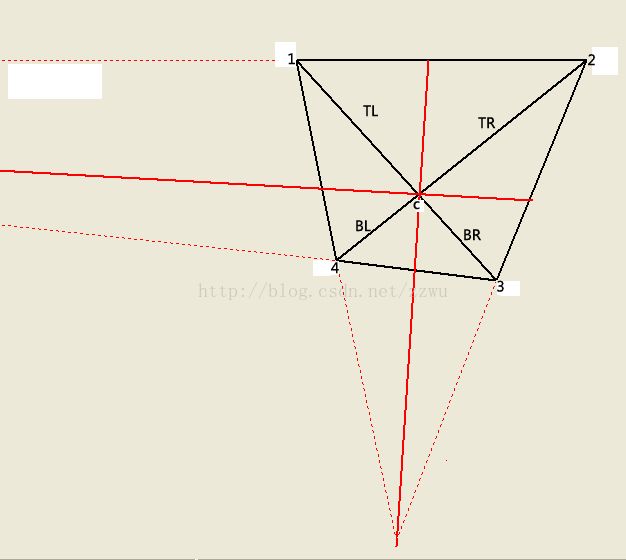
  四分,就是将幕布的投影四边形分成

                   左上(TL),右上(TR),左下(BL),右下(BR)

四部分. 如下图中, 由1-2-3-4四点组成的四边形被水平线分成上下,被垂直线分成左右,整个四边形就有了TL,TR,BL,BR四部分:    

 3.任意四边形如何进行四分? 

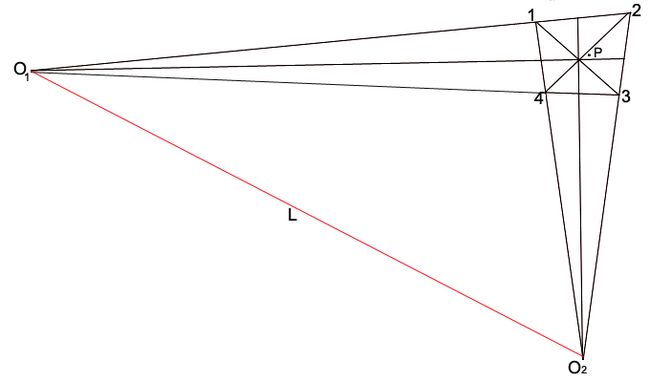
 *将四边形的两对对边连起来,它们或者平行,或不平行。如不平行,求其交。

  如上图,因12与34不平行,故可得交点O1; 14与23也不平行,故有交点O2。

 

 *求四边形的两个对角线13,24的交点C;

 

 *通过O1,C作水平线Lh=O1-C, 如无O1,则通过C作12(或34)的平行线,为Lh;

 

 *通过O2,C也作垂直线Lv=O2-C, 如无O2,则通过C作13(或24)的平行线,为Lv;

 

 *Lh和Lv就可将四边形1234划分为四部分。

 

4.四分法如何进行? 

 

 *确定幕布上点P在投影四边形的象限(TL,TR,BL,BR之一)

 

 *将幕布上点P所在象限,定为显示屏对应点P'所在象限;

 

 *将所得象限作为四边形,再作四分,再定为P'在显示屏的象限;

 

 *不断重复,直到显示屏的象限收敛为一个象素为止,就结束.  

 

Top 

35.  回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-24 09:00:45Z  得分:0

  

感谢大家，我越来越看不懂了  :)

等到问题解决，我的程序搞定，就再来散上500分。

我看不懂各位解答，也不知道程序该怎么写。而且程序要求最多在10毫秒就要算出一个坐标，昏啊。

 

Top

 

36.  回复人： zzwu(未名) ( ) 信誉：106  2002-07-24 10:13:28Z  得分:0

 

 写程序要用到一些几何作图,包括连线,求交,判别一点在一线的哪一侧.然后就是组织循环.好像没有更多的事情要作了.

 

我不知道的一个事情是:

 你的幕布是什么样的幕布?

 幕布上的点的位置如何读入到计算机中?

 

我想看看大家(特别是quicmous)对我的方法有无意见和疑问? 如1-2天内没有问题提出,接下来就让我用Delphi来编出此程序.

 

Top

 

 37. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-24 11:13:23Z  得分:0 

 

我只在开始时候进行一次校准，就是给出四个顶点的坐标。然后就是随便在幕布上点，我要快速的把这个点画在计算机屏幕上。

刚才想了一下，可以先求出1024等分幕布上区域的斜率或者距离，然后后来的点到这个数组里面查找自己最接近的位置。这样每次运算的时间大大降低，代价是16K的存储空间。

我想这个数组内容应该是有规律的吧？怎么求出这个规律呢，就能不用这16K了。

实际上从幕布取得值有很多方法啊，红外线、超声波、压感等等，各种方法都有广泛的应用，比如触摸屏、手写板、描图板。

 

 

Top

 

 38. 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-24 16:45:41Z  得分:0 

 

to zzwu(未名) :

  我担心你的计算量仍然很大。一劳永逸的方法是把方程解出来，可计算量也太大。是不是让 tony1978(突击召唤师) 请我们下一次馆子犒劳一下...

 

 

Top

 

 39. 回复人： zzwu(未名) ( ) 信誉：106  2002-07-24 21:00:18Z  得分:20 

 

quicmous(快鼠):

 

   好呀! 到上海来,去附近小摊上每人吃一碗凉粉,这样3个人差不多就是500分,不够的话,我来请客!

 

   言归正传, 你说的,把方程解出来，我想也是办法, 可以一试, 计算量我想不会太大,因为这是'一步到位'了.

 

   用我所讲的办法,编程方便些,需要循环,但总共迭代log2(1024)=10次,如每次作20个乘法,20个加法,应是很快的.

 

   另外,不理解tony1978(突击召唤师)对速度的要求,要知道,幕布上去定点不是人工操作吗,何必需要速度?

 

   还是让我先编个程序出来再说吧.

 

 

Top

 

 40. 回复人： xf8zbf(瞎想) ( ) 信誉：100  2002-07-24 21:51:40Z  得分:0 

 

说只要三个点的笨笨们，你们看那四个点是空间中的三维点吗？

那只是平面上的四个点啊！

 

所以四个点是必须的。

至于是否必须要九个点，我倒是不能一下肯定 

 

Top

 

 41.  回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-24 22:14:06Z  得分:0 

 

to zzwu(未名):

tony1978(突击召唤师)时想做一个类似触摸屏的系统，用户在投影上选择一个点，程序马上就能换算出屏幕坐标。

你是否听说过有一种激光键盘，就是利用激光把键盘的影像投在桌面上，用户的按键动作会反馈到计算机转换成ASCII码。

不过对速度的要求和精度的要求有可能是一种更高级的设备，既然这个最基本的问题都解决不了，干脆放弃项目吧...呵呵!!

 

  

Top

 

 42. 回复人： zzwu(未名) ( ) 信誉：106  2002-07-25 08:56:21Z  得分:0 

 

tony1978(突击召唤师):

 

  我希望你本人来谈谈实际使用的设备,使我能确信考虑速度的必要性.

 

  如果是通过人工点入幕布上点的位置,就根本用不到提任何速度指标. 

 

Top

 

 43. 回复人： zzwu(未名) ( ) 信誉：106  2002-07-25 09:21:55Z  得分:0 

 

tony1978(突击召唤师):

 

    另外,也希望讲讲'越来越看不懂'的具体事情在何处?

 

    说不定其中确实有问题,也就是任何人实际都无法看懂的问题.

 

    如果这一问题存在于我的算法中,我就应改正它,这也就是为什么要大家先看看我的算法的原因.

 

    如果你所看不懂的问题实际不是问题,但存在于我的算法中,我将进行说明.你是最终用户,要心里有底才行.

  

Top

 

 44. 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-25 10:10:17Z  得分:0 

 

为什么我认为三个点就行，三点定一平面，当然行了

而且是点光源才是EASY呢

做一图

  ＊

 -----

 /    /

------

 -----------

/ ＊      /

-----------

定光源点为L

定左下角为下面平面Q

上面平面左下角为Q'

给 出了下面一点A

做光源到下面点的直线，交上面平面点A'

做AQ与A'Q'

做

LQ交上面平面为Q'（这是一定的，也是题义直接就有了）

则LA'Q'与LAQ为确定形

证毕（三点就行）

解：

做过Q'点一平面与下平面平行  阿尔法'

得出A''点，

再用A''点解出A'

可解

 

程序：

自己写写

分数：

你看着给

TO上面朋友，

我还真是笨笨！！

 

 

 

Top

 

 45. 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-25 10:23:51Z  得分:0 

 

对了，考虑到大家把高一的立体几何忘了，

还得写一点，

用A''点解A'点

已知两平面夹解为 伽马

平面上方一点为L

做LA''交另一平面为A'

求A'点

解：

做L到两平面相交线的垂线，垂点为O

做OA''和OA'

在OLA'的平面上解三角形

相当于已知一三角形，从一点做一夹解为 伽马的线交对边为一点X

解X

一题

（已经是平面的问题了）

 

对了，效率么，当然没的说，

你把已知条件都设为变量，解出公式来，

用计算机一算，肯定是慢不了，

不过，你的解的过程（时间做废）

哈哈，是不是有点老板的作风？？？

 

 

 

Top

 

 46. 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-25 11:14:57Z  得分:0 

 

头一次参与这么热烈的讨论啊，呵呵。

我的设备是每秒扫描50-60次，如果有人在幕布上模拟鼠标拖拽，就要在20毫秒内返回。同时，由于还要更新屏幕、给硬件留出缓冲时间，所以时间就更少了。

zzwu(未名) 的算法，在我的机器（PIV 1.4G 512M）上，大概不到1毫秒，符合要求。可是在最低配置要求下，就很困难了。

我已经三年没看过算法了，所以现在看起来很头疼，程序也不会编了  :)

我的程序框架已经设计好了，估计到9月末开始编码。设备现在还在设计中，据我乐观的估计，是赚不到钱  ft~~~~~

 

 

Top

 

 47. 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-25 11:21:50Z  得分:0 

 

对了，考虑到大家把高一的立体几何忘了，

还得写一点，

用A''点解A'点

已知两平面夹解为 伽马

平面上方一点为L

做LA''交另一平面为A'

求A'点

解：

做L到两平面相交线的垂线，垂点为O

做OA''和OA'

在OLA'的平面上解三角形

相当于已知一三角形，从一点做一夹解为 伽马的线交对边为一点X

解X

一题

（已经是平面的问题了）

 

对了，效率么，当然没的说，

你把已知条件都设为变量，解出公式来，

用计算机一算，肯定是慢不了，

不过，你的解的过程（时间做废）

哈哈，是不是有点老板的作风？？？ 

 

Top

 

48. 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-25 11:30:28Z  得分:0 

 

纯数学有的时候，是很好用的， 

 

Top

 

 49. 回复人： zzwu(未名) ( ) 信誉：106  2002-07-25 13:08:15Z  得分:0 

 

tony1978(突击召唤师):

 

通过你的解释,我对此问题已有了解,这确是一个创新工作,至少我以前没有看到过,甚至也没有想到过,我认为是一项有意义的课题,赚不到钱也值得做,成功后,可以去申请一个专利麽.

 

到时不要忘了我们大家呀!

 

 

Top

 

 50.回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-25 15:54:03Z  得分:0 

 

tony1978(突击召唤师):

我这两天有点焦头烂额，等我忙完手头的活，如果 zzwu(未名) 等高手还没出手，我就费劲给你一个基于直角坐标系的解,我真心的希望你的发明能挣到钱!

 

 

Top

 

 51.回复人： xf8zbf(瞎想) ( ) 信誉：100  2002-07-25 20:33:20Z  得分:0 

 

(0,1),(0,0),(1,0),(1,1)

 

一 对应(0,1),(0,0),(1,0),(1,1)

 

二 对应(0,1),(0,0),(1,0),(2,2)

 

设两平面平行，高为1

则一为立方体

二为。。。

 

总之可以得到两种形状的物体。

 

 

上下两平面的点可以有一一对应关系呀

 

 

 

Top

 

 52.回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-27 08:43:27Z  得分:0 

to zzwu(未名) :

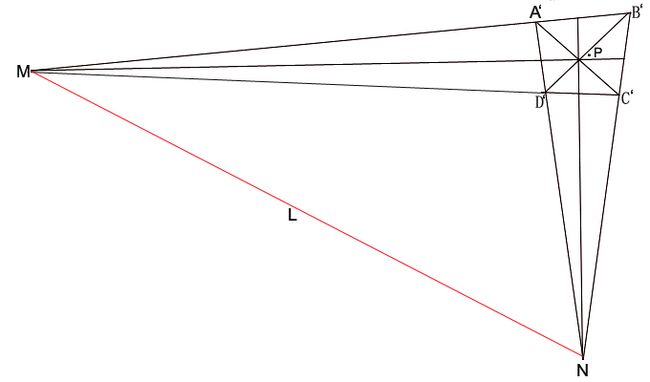
  我发现一个简单解法。方法如下：

  假设原像是矩形 ABCD , 像A'B'C'D'.不失一般性,假设A'B',D'C'相交于M, A'D',B'C'相交于N. 过A作直线L于MN平行.

  如果AB上有均匀(等距)的刻度,则些刻度在A'B'上不再均匀.如果以N点为光源,把 A'B'映射到直线L上,则这些刻度再次变成均匀(等距)的.

   因此,欲确定像平面内任意一点的横坐标,只需要把该点通过光源N映射到直线 L上即可.同理,以M点为光源可以求得纵坐标.

   至于如何根据像点在L上的位置换算成计算机屏幕坐标,方法有很多,例如定比分点或直接采用比例算法等等.

   呵呵,我想我们已经找的了最佳的算法.

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-27 09:31:36Z  得分:20

 

 

 

若假设是线性变换，这里提供一种方法--同素变换法。

同素变换是线性变换之一，但变换前后不保持线段的长度比和平行性，符合空间线性影射关系。

  设原始点为：（x,y）

   投影点为：（X,Y）

  则有

     X=（a1*x+a2*y+a3）/(c1*x+c2*y+c3)

     Y=（b1*x+b2*y+b3）/(c1*x+c2*y+c3)

  可简化为

     X=（a1*x+a2*y+a3）/(x+d2*y+d3)

     Y=（b1*x+b2*y+b3）/(x+d2*y+d3)

  式中  d2=c2/c1, d3=c3/c1

  共8个未知系数（a1,a2,a3,b1,b2,b3,d2,d3），只需4对点的条件，于是不难解出。整屏图形计算系数只需一次，不会影响速度。

 

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-27 12:57:48Z  得分:0

 

 

 

*****上文重写******

 

若假设是线性变换，这里介绍一种方法----同素变换法。

同素变换是线性变换之一，但变换前后不保持线段的长度比和平行性，符合空间线性影射(透视)关系。

  设幕布点为：（x,y）

   屏幕点为：（X,Y）

  则有

     X=（a1*x+a2*y+a3）/(c1*x+c2*y+c3)

     Y=（b1*x+b2*y+b3）/(c1*x+c2*y+c3)

  分子分母同除c1,上式可简化为

     X=（a1*x+a2*y+a3）/(x+c2*y+c3)

     Y=（b1*x+b2*y+b3）/(x+c2*y+c3)

  式中 a1=a1/c1,a2=a2/c1,a3=a3/c1,b1=b1/c1,b2=b2/c1,b3=b3/c1,c2=c2/c1,c3=c3/c1

  共8个未知系数（a1,a2,a3,b1,b2,b3,c2,c3），只需4对已知点的条件（屏幕及幕布图形各四个顶点），于是不难解出8个系数。整屏图形，计算系数只需一次，不会影响速度。

 

 

 

Top

 

回 复人： zzwu(未名) ( ) 信誉：106  2002-07-29 09:20:00Z  得分:0

 

 

 

To quicmous(快鼠):

 

  你的最后一个算法十分巧妙! 如果不是联想到视平线,视平面等透视原理,要利用投影几何的基本知识来直接证明算法的正确性还真不容易!

 

  我也同意你的看法:这已经是一个最优方案了,不再可能找到更多的改进余地.

 

  另外,不知你有没有注意到前面Xqr()提出的'同素变换法'? 他和我们走的是两条路,采用了代数方法来实现映射. 但我想(没有具体去算过,我很懒的动笔),如果他的变换法没有问题的话, 他的结果应和你的结果一致, 也就是说,把你的方案综合起来写成表达式,很有可能和他的X,Y的算式完全一样.

 

 

 

To tony1978(突击召唤师):

  我前面提出的那个方案已编写成了一个程序,可以演示.为了方便,采用DOS下640*480的标准VGA图形模式,用pascal语言.由于分辨率低,再加上想在屏幕上画出两个无穷远点,幕布的面积已很小,所以我只迭代6次.

  程序利用到我以前编的一些程序(改编得到),有一大堆无关的东西还在上面,相当乱. 所以源程序要整理干净才能发给你或在这里贴出.

 

 

 

Top

 

 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-29 14:43:04Z  得分:0

 

 

 

To quicmous(快鼠):

绝妙的方法！不过有两条线平行的时候怎么办啊？

 

 

Top

 

 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-07-29 15:45:23Z  得分:0

 

 

 

六元的方程组，怎么解啊。

 

 

Top

 

 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-29 16:07:23Z  得分:0

 

 

 

To zzwu(未名) ：

  xqr() 的方法和我以前列出的方程是等价的，难点在于解这个方程组并不容易。新的方案完全变成了平面解析几何问题，计算应该简单一些。

 

to tony1978(突击召唤师) :

A'B'||D'C'时，L||A'B'，这个时候A'D方向的坐标（可能是纵坐标）应该采用某种比例算法就可以确定。

 

 

Top

 

 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-29 16:55:17Z  得分:0

 

 

 

quicmous(快鼠)

你的方法真是好，

可惜要两个平面平行才行呀，

这和相似有分别么？

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-29 16:57:43Z  得分:0

 

 

 

同素变换又称共线变换。为求未知系数，须要解8阶的线性方程组，解线性方程组的算法在计算方法一书中早有现成，不管方程组有多少阶，编程代码都一样而且很简练。一旦求出8个系数，计算屏幕坐标则易如反掌。同素变换法的编码具有简洁易读易维护的优点。

quicmous(快鼠)的方法基于透视原理的图解算法，亦很好，但各种判断和特殊处理过程可能较多。

 

 

 

Top

 

 回复人： dearmite(笨笨的我*_^) ( ) 信誉：100  2002-07-29 17:00:36Z  得分:0

 

 

 

quicmous(快鼠)

你没看我的贴子，

你这个方法和我第一步一样，

另，如两平面夹解很小，就统一除以cos(F)

可以说，这样就是你的方法的修正解，

但如楼主要想算，只好把两二步，用几何推一下了（其实不难的，

写起来多，算起来，就那么两下（斜对直，下投影））

 

 

Top

 

 回复人： zzwu(未名) ( ) 信誉：106  2002-07-29 17:36:56Z  得分:0

 

 

 

to tony1978(突击召唤师):

作平行线在投影几何里和过两点连直线是同一概念.搬到欧氏几何中才有本质区别.

具体解决办法就是分别考虑,如和我前面讲的那样.

 

-----------------------------------------------------------------

to dearmite(我是笨笨!):

为什么要两个平面平行才行啊？

 

-----------------------------------------------------------------

to xqr()：

我很想稍微再深入了解一点你的同素变换法,不知属于那一数学领域的,以前好像听到过,是代数几何吗?

又:

在我完成了我的算法的同时,也就完成了quicmous(快鼠)算法所需的几个主要子程序,这一算法实现起来实际也并不太复杂.

 

 

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-30 07:50:06Z  得分:0

 

 

 

to zzwu(未名)：

 

同素变换又称共线变换，属射影几何范畴，常用于地图图形的几何改正，其它领域应用不多见。其实，同素变换是二维图形空间线性变换的代数形式，可从二维齐次坐标矩阵变换公式(见下式)演变而来。

   （X' Y' H）=（x y 1）T

   式中，T是3*3变换矩阵，最后一列不是(0 0 1),而是任意数(p q s)

   H=px+qy+s

   X=X'/H, Y=Y'/H

 

本人曾参阅下列各书：

1.几何变换  龙泽斌编著，湖南科技出版社，1984

2.空间解析几何引论  南开大学数学系编，人民教育出版社，1978

3.计算机地图制图原理  徐庆荣等编著，武汉测绘科技大学出版社，1993

 

 

 

Top

 

 回复人： zzwu(未名) ( ) 信誉：106  2002-07-30 15:45:25Z  得分:0

 

 

 

 

To xqr(): 很感谢!

 

<射影几何>我手头有一本老的英文书,前几天我正在看,很有趣,也是受它的启发,提出了前面那个算法. 这本书的缺点是不讲变换的,看不到一个矩阵,都用1-1对应和几何图形来说明问题.

 

南开的<空间解析几何引论>正好自己有,但一下子没有找到上册. 在下册有个'射影几何简介',粗翻了一下没有找到,准备再细心点看一看.

 

<计算机地图制图原理>则完全没有了,只得明天去图书馆找了.

 

再次谢谢你了.   

 

 

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-30 17:43:45Z  得分:0

 

 

 

to zzwu(未名)：

 

谈谈我的认识。

1.在有关射影几何的书中可能找不到“同素变换”或“共线变换”的名词，但是这种变换方法或思想是有的。在《几何变换》的“几何变换的矩阵方法”一章中对此法谈得多些具体些。所谓“同素变换”或“共线变换”的称法我猜测可能是地图学界给它起的。

2.实际上，同素变换是将位于z=0平面上的图形变换至z=1的平面上，并保持线性关系。其变换过程似中心(透视)投影，但变换前后两图形平面总是平行的，故不同于一般的中心投影。其次，变换前后图形线段不具有等比性和平行性，故又不同于仿射变换。

3.鉴于上述，在纯中心(透视)投影条件下，采用同素变换只是一种近似处理。

 

以上浅见，请指正。

 

 

 

Top

 

 回复人：quicmous(快鼠) ( ) 信誉：99  2002-07-30 20:31:18Z  得分:0

 

 

 

to zzwu(未名)：

 xqr() 提供的变换与我前面给出的变换是等价的。都是先把z=0平面上的图像经过一个线性变换变到一个三维空间的中间位置，然后把该图形映射到z=1平面上。不同之处是，xqr()直接略去了z和z'坐标，方程显得更为简练。

 

以下选自我在楼上法的帖子，可以和xqr的防城进行比较：

...

我给出的变换包含两个基本变换：

第一步：把位于xy平面上的屏幕坐标经过仿射变换转换到三维坐标系。这个变换本身包含平移、旋转等几何变换。

第二步：以三维坐标原点为光源的投影变换，投影平面是z=1,公式如下P(x,y,z)->p'(x',y',z')

   x'= x/z

   y'= y/z

...

x'=(a11*x+a12*y+a13*z+a14)/(a31*x+a32*y+a33*z+a34)

y'=(a21*x+a22*y+a23*z+a24)/(a31*x+a32*y+a33*z+a34)

...

断定原像平面和像平面平行，其实是误解，因为原像到像的变换是一个线性变换和摄影变换构成的复合变换。首先原像经过一个线性变换得到位置可能很“别扭”的中间像，中间像再投影到z=1平面上。正如你能看到的，我在楼上帖子里的方程式是非线性的（射影变换）。

...

 

计算机算法手册确实给出了解线性方程组的一般方法，问题是如果对于每一个点都要采用复杂的消元法求解，效率会成问题。因此问题的关键在于每个点坐标变换的计算效率。

 

 

Top

 

 回复人： zzwu(未名) ( ) 信誉：106  2002-07-31 10:03:42Z  得分:0

 

 

 

上面两位: 谢谢帮助!

   我也深信,无论我们用什么方法,只要都能正确解决问题,那么所作的变换一定都是同一种变换!

   我所好奇的,是'同素变换'这个术语,以前没有听到过,所以想了解一下起来源.是从哪一实际应用领域提出来的?

   昨晚我碰到一位一生从事几何研究的几何教研组的老师,问起'同素变换'的问题. 他也说没有听到过,并'估计不会是一个数学术语',并且,正如xqr()所预料那样,'可能来自地图学界的'.

 

 

 

 

 

Top

 

 回复人： zzwu(未名) ( ) 信誉：106  2002-07-31 10:44:03Z  得分:0

 

 

 

to xqr():

 

关于原像平面和像平面平行的问题,我也同意quicmous(快鼠)的看法,认为不需要.

 

因为,我想,如果原像平面和像平面平行,则幕布上的图像也就不会被弄成任意四边形了.

 

 

 

 

Top

 

 回复人： xqr(星球人) ( ) 信誉：100  2002-07-31 13:06:48Z  得分:0

 

 

 

to zzwu(未名)

to quicmous(快鼠)

 

再噜囌几句。

同素变换的矩阵表达式为：

  （X' Y' H）=（x y 1）T

  H=px+qy+s

  X=X'/H, Y=Y'/H

  式中，T是3*3变换矩阵，第1，2列的作用是仿射变换（比例，对称，错移，旋转，平移等），最后一列(p q s)的作用是中心透影变换和全图比例变换。

  分解上式的过程：

  1.将xoy平面上的图形平移至z=1的平面，即(x y 0)->(x y 1)   

  2.将z=1平面上的图形(z y 1)仿射变换至H=px+qy+s的平面上，即

     (x y 1)->（X' Y' H）  

  3.以坐标原点为透视中心，对H=px+qy+s平面上的图形点（X' Y' H）作射线，并用z=1的平面截取得z=1平面上新图像，即（X' Y' H）->(X'/H  Y'/H 1)=(X Y 1)，X和Y便是我们所需要的。

  可见

  1.上述结果图像平面与原图像平面的平行，只是为了公式推导的图解映射关系，并不代表两图像平面的真实关系。注意，它与两个平行平面间的中心投影变换不同，它不保持等比和平行性，成像仍可能为任意四变形，在实际应用中也不要求两个像平面要平行才能采用同素变换。

  2.同素变换是仿射变换和中心变换的复合变换。

 

--------------------------------------------------------------------

to quicmous(快鼠)

 

按同素变换，整屏图形，计算系数（8个）只需一次（因为全图是同一种变换），不须每图形点都要重新算一次系数。在求得系数（a1,a2,a3,b1,b2,b3,c2,c3）后，每个图形点的计算量甚小，如下式

   X=（a1*x+a2*y+a3）/(x+c2*y+c3)

   Y=（b1*x+b2*y+b3）/(x+c2*y+c3)

 

 

 

 

Top

 

 回复人： quicmous(快鼠) ( ) 信誉：99  2002-07-31 16:27:29Z  得分:0

 

 

 

to xqr() :

 8个系数只需一次计算，同意你的说法。

 

 

Top

 

 回复人： zzwu(未名) ( ) 信誉：106  2002-07-31 17:46:06Z  得分:0

 

 

 

to 大家:

   

   这样好像都能统一了!

 

   我的演示程序也可以了,如有兴趣看,我发给大家.

 

 

   确实非常快非常快,6次乘,2次除,再是几次加,就整个完了!

 

 

 

 

Top

 

人： xqr(星球人) ( ) 信誉：100  2002-08-01 06:11:28Z  得分:0

 

 

 

to zzwu(未名)

to quicmous(快鼠)

十分感谢你们对我的许多启示。

我们提出的具体解决办法虽有些不同，但思路和基本原理是一致的。

 

 

Top

 

 回复人： hanqiong1(瀚琼) ( ) 信誉：97  2002-08-05 13:32:04Z  得分:0

 

 

 

不知诸位是否做过从一张图片上识别一维条形码的程序或算法。我急切需要。

联系方式：

[email protected]

 

 

Top

 

 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-08-23 16:29:05Z  得分:0

 

 

 

结贴，FAQ之

 

 

Top

 

 回复人： tony1978(突击召唤师) ( ) 信誉：100  2002-08-23 18:01:50Z  得分:0

 

 

 

上个论坛，比上火星都慢

 

 

Top

 

 

 

该问题已经结贴 ，得分记录：

 eion (5)、 quicmous (20)、 eion (20)、 jojoship (5)、 zzwu (20)、 dearmite (10)、 xqr (20)、 

 

 

 

 

 回复人： xqr(星球人)