回归算法 逻辑斯谛回归(LR算法)

回归算法 LR算法

二分类(Logistic Regression 逻辑斯谛回归 简称LR)：model -> 0/1

多分类(Softmax)：model -> 0/1/2…

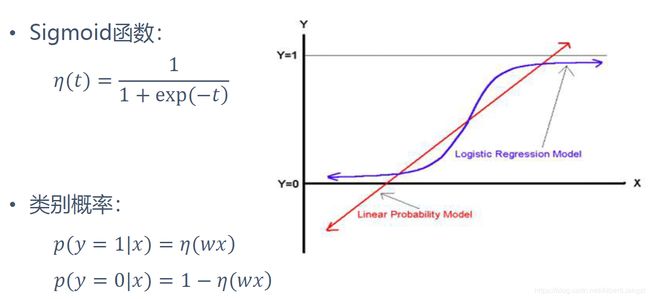
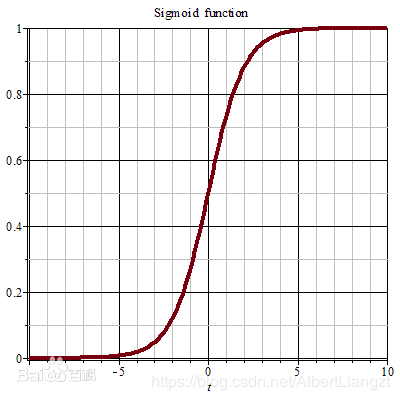
一、Sigmoid函数——逻辑回归的实现

1.

2.用sigmoid原因：

• 简单来讲，可以将(-∞, +∞)的输入变量映射到(0,1)，作为后验概率
• 在某个临界点左右两端变化较大，比较容易进行分类

二、基本公式推导

1.对sigmoid求w偏导：

$\eta (t)=\frac{1}{1+e^{-t}}$ 转换为 $\eta (wx)=\frac{1}{1+e^{-wx}}$

偏导为$\frac{\partial (\eta )}{\partial (w)}$ $=\frac{(-1)}{(1+e^{-wx}){2}} (-x)(e^{-wx}) $

$=\frac{1}{1+e^{-wx}}\ast \frac{e^{-wx}}{1+e^{-wx}}\ast x$

$=\frac{1}{1+e^{-wx}}\ast \frac{1+e^{-wx}-1}{1+e^{-wx}}\ast x$

$=\frac{1}{1+e^{-wx}}\ast (1-\frac{1}{1+e^{-wx}})\ast x$

$=\eta \ast (1-\eta )\ast x$

2.对损失函数$L(w)$求导（梯度）：

2.1类别概率

$p(y_i=1|x)=\eta$
$p(y_i=0|x)=1-\eta$

2.2似然函数

$L(w)=\prod _{i}p(y_i)$
$=\prod _i(I(y_i=1)p(y_i=1|x_i,w))\ast I(y_i=0)p((y_i=0)|x_i,w))$
$=\prod _i{y}_i\eta \ast (1-y_i)(1-\eta )$

2.3负对数似然

$log(L(w))=-log(\prod _i{y}_i\eta \ast (1-y_i)(1-\eta ))$
$log(L(w))=-\sum _i(y_{i}log(\eta )+(1-y_i)log((1-\eta ))$

也写作

$L(w)=-\sum _i(I(y_i=1)log(p(y_i=1|x_i,w)))+I(y_i=0)log(p((y_i=0)|x_i,w)))$
$=-\sum _i(I(y_i=1)log(\eta (w{x}_i))+I(y_i=0)log(1-\eta (w{x}_i)))$

2.4所以负对数似然求偏导

$$\delta (L(w))=-\sum (\frac{y_i}{\eta }\eta (1-\eta )x_i-\frac{1-y_i}{1-\eta }\eta (1-\eta )x_i)$$
$$=-\sum (y_i(1-\eta )x_i+(1-y_i)\eta x_i)$$
$$=-\sum (y_i{x}_i-y_i\eta x_i-\eta x_i+y_i\eta x_i)$$
$$=-\sum (y_i-\eta )x_i$$

所以梯度为:$\nabla (L(w))=-\sum (y_i-\eta )x_i$

三、举例：到达谷底的最佳路线

梯度

梯度方向——让f(x,y)函数快速变大的方向
反梯度方向——让f(x,y)函数快速变小的方向

方法：梯度下降法——最小化F(w)

• 1.设置初始w，计算出F(w)
• 2.计算梯度$\nabla$：下降方向dir=(-$\nabla$F(w))
• 3.尝试梯度更新：$w^{new}=w+步长\ast dir$
  得到下降后的$w^{new}$和F($w^{new}$)
• 4.如果F($w^{new}$)-F(w)较小：说明基本处于底部，模型稳定，可以停止
  否则w=$w^{new}$, F($w^{new}$)=F(w)

实现

误差=真实值-预测值=(yi - $\eta (w{x}_i)$)
errors = target - prediction
prediction = sigmoid(wx)=(wx)
wx = weight * x + b
$w_1$：随机初始化 => f(x)：预测值

python实现

git地址