VINS-Mono之外参标定和视觉IMU联合初始化

1.前言

本博客主要介绍VINS-Mono初始化时相机与IMU对齐，主要包括相机到IMU的外参估计、陀螺仪偏置、相机位移和估计空间点的尺度、重力加速度、每帧速度，主要参考了深蓝学院的VIO课程及博客VINS-Mono理论学习——视觉惯性联合初始化与外参标定和崔华坤的《VINS 论文推导及代码解析》。
总体而言，视觉IMU对齐流程主要包括以下几部分：

1. 若旋转外参数$q_c^b$未知，则先估计旋转外参数
2. 利用旋转约束估计陀螺仪偏置：$$q_{b_k}^{c_0}=q_{c_k}^{c_0}\otimes (q_c^b{)}^{-1}$$
3. 利用平移约束估计重力方向，速度，以及尺度初始值$$s{\bar{p}}_{b_k}^{c_0}=s{\bar{p}}_{c_k}^{c_0}-R_{b_k}^{c_0}{p}_c^b$$
4. 对重力向量$g^{c_0}$进行进一步的优化
5. 求解世界坐标系$w$和初始相机坐标系$c_0$之间的旋转矩阵$q_{c_0}^w$，并将轨迹对齐到世界坐标系中

2. 外参标定 (利用旋转约束估计外参数旋转$q_c^b)$

相邻俩时刻$k$,$k+1$之间，$k$时刻的IMU到$k+1$时刻的相机外参旋转矩阵有：$$R_{c_{k+1}}^{b_k}=R_{b_{k+1}}^{b_k}\cdot R_c^b=R_c^b\ast R_{c_{k+1}}^{c_k}$$ 转换为四元素有： $$q_{b_{k+1}}^{b_k}\otimes q_c^b=q_c^b\otimes q_{c_{k+1}}^{c_k}$$ 上式可写为：$$(\mathcal{L}(q_{b_{k+1}}^{b_k})-\mathcal{R}(q_{c_{k+1}}^{c_k}))q_c^b=Q_{k+1}^k\cdot q_c^b=0$$
将多个时刻的上式方程累计起来，并加上鲁棒核权重，可构建超定方程：$$\left[\begin{array}{c}{w}_1^0\cdot Q_1^0\\ w_2^1\cdot Q_2^1\\ \cdots \\ w_N^{N-1}\cdot Q_N^{N-1}\end{array}\right]q_c^b=Q_N\cdot q_c^b=0\text{\hspace{1em}(1)}$$ 其中：
$$w_{k+1}^k=\{\begin{array}{c}1,r_{k+1}^k<threshold\\ \frac{threshold}{r_{k+1}^k},otherwise\end{array}$$ 由旋转和轴角之间的关系$tr(R)=1+2\cos \theta$，能得到角度误差$r$的计算为：$$\begin{gathered} r_{k+1}^k=acos((tr((R_{b_{k+1}}^{b_k}{\hat{R}}_c^b{)}^{-1}{\hat{R}}_c^b{R}_{c_{k+1}}^{c_k})-1)/2) \\ =acos((tr({\hat{R}}_c^{b-1}{R}_{b_{k+1}}^{b_k-1}\widehat{R_c^b}{R}_{c_{k+1}}^{c_k})-1)/2) \end{gathered}$$
公式(1)的求解同样采用SVD分解，即最下奇异值对应的奇异向量即为IMU坐标系到相机坐标系的旋转(四元素表示)，具体代码见initial_ex_rotation.cpp 函数 CalibrationExRotation()

---

对于$tr(R)=1+2\cos \theta$的推导如下：
旋转矩阵和轴角的关系为：$$R=\cos \theta I+(1-\cos \theta )a{a}^T-\sin \theta [a{]}_{\times }$$ 其中$a=[a_1,a_2,a_3{]}^T$为单位旋转轴，$\theta$为绕着旋转轴转动的角度，$[a{]}_{\times }=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]$
同时，由于$a$为单位旋转轴，有$tr(a{a}^T)=1$，故：
$$\begin{gathered} tr(R)=\cos \theta tr(I)+(1-\cos \theta )tr(a{a}^T)+\sin \theta tr([a{]}_{\times }) \\ =3\cos \theta +(1-\cos \theta )=1+2\cos \theta \end{gathered}$$ 同时也有$Ra=a$，即旋转轴上在旋转后并不发生变化，旋转轴$a$为旋转矩阵$R$的特征值为1对应的特征向量。
关于旋转矩阵和轴角的关系可参考：https://en.wikipedia.org/wiki/Rotation_matrix

---

3. 视觉IMU联合初始化

假如我们已经有一个初始的IMU到相机的外参$T_c^b=[R_c^b|p_c^b]$，同时又有不同时刻帧的位姿$T_{c_k}^{c_0}=[R_{c_k}^{c_0}|p_{c_k}^{c_0}]$ (基于第一帧坐标系下)，那么我们可以知道姿态从相机坐标系到IMU坐标系的关系$T_{bk}^{c_0}=[R_{b_k}^{c_0}|p_{b_k}^{c_0}]$与前俩者的关系：$$T_{c_k}^{c_0}=T_{b_k}^{c_0}{T}_c^b$$ 则有：$$\left[\begin{array}{cc}{R}_{c_k}^{c_0}& s{\bar{p}}_{c_k}^{c_0}\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}{R}_{b_k}^{c_0}& s{\bar{p}}_{b_k}^{c_0}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}{R}_c^b& p_c^b\\ 0& 1\end{array}\right]$$ 将式子展开有【论文公式(14)】：$$R_{c_k}^{c_0}=R_{b_k}^{c_0}{R}_c^b\to R_{b_k}^{c_0}=R_{c_k}^{c_0}(R_c^b{)}^{-1}$$ $$s{\bar{p}}_{c_k}^{c_0}=R_{b_k}^{c_0}{p}_c^b+s{\bar{p}}_{b_k}^{c_0}\to s{\bar{p}}_{b_k}^{c_0}=s{\bar{p}}_{c_k}^{c_0}-R_{b_k}^{c_0}{p}_c^b\text{\hspace{1em}(2)}$$
视觉IMU联合初始化中的视觉SFM位姿与IMU位姿的对齐主要在vins_estimator/src/initial/initial_aligment.cpp中的VisualIMUAlignment()函数中。

3.1 陀螺仪偏置的估计 (利用旋转约束估计$b_w$)

对于窗口的连续俩帧$b_k$和$b_{k+1}$，已经从SFM中得到了旋转$q_{b_k}^{c_0}$和$q_{b_{k+1}}^{c_0}$，从IMU预积分中得到了相邻帧的旋转${\hat{\gamma }}_{b_{k+1}}^{b_k}$。根绝约束方程，联立所有相邻帧，可以得到最小化代价函数【论文公式(15)】:
$$\underset{\delta b_w}{\min }\sum _{k\in \mathcal{B}}{\Vert q_{b_{k+1}}^{c_0-1}\otimes q_{b_k}^{c_0}\otimes {\gamma }_{b_{k+1}}^{b_k}\Vert }^2\text{\hspace{1em}(3)}$$ 其中$\mathcal{B}$为滑动窗口内的所有图像帧，另外对预积分进行一阶泰勒展开近似，即对其线性化：$${\gamma }_{b_{k+1}}^{b_k}\approx {\hat{\gamma }}_{b_{k+1}}^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{J}_{b_w}^{\gamma }\delta b_w\end{array}\right]\text{\hspace{1em}(4)}$$ 由于在理想情况下，即当$q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}={\gamma }_{b_{k+1}}^{b_k}$，这俩个旋转的差异$(q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}{)}^{-1}{\gamma }_{b_{k+1}}^{b_k}$的旋转角度为0，根据四元素的表示，可得虚部为$0$，实部为1：$$q_{b_{k+1}}^{c_0-1}\otimes q_{b_k}^{c_0}\otimes {\gamma }_{b_{k+1}}^{b_k}=\left[\begin{array}{c}1\\ 0\end{array}\right]$$ 则有：$${\gamma }_{b_{k+1}}^{b_k}=q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}\otimes \left[\begin{array}{c}1\\ 0\end{array}\right]\text{\hspace{1em}(5)}$$ 将公式(4)代入公式(5)，得：$${\hat{\gamma }}_{b_{k+1}}^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{J}_{b_w}^{\gamma }\delta b_w\end{array}\right]=q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}\otimes \left[\begin{array}{c}1\\ 0\end{array}\right]$$ 当只考虑虚部(虚部为三维向量)的时候，我们有：$$J_{b_w}^{\gamma }\delta b_w=2{\lfloor {\hat{\gamma }}_{b_{k+1}}^{b_k-1}\otimes q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}\rfloor }_{xyz}$$ 将左边转为对称矩阵，这样就可以直接用LDLT对系数矩阵进行分解了：$$J_{b_w}^{\gamma T}{J}_{b_w}^{\gamma }\delta b_w=2J_{b_w}^{\gamma T}{\lfloor {\hat{\gamma }}_{b_{k+1}}^{b_k-1}\otimes q_{b_k}^{c_0-1}\otimes q_{b_{k+1}}^{c_0}\rfloor }_{xyz}\to Ax=b$$ 求出陀螺仪的偏置bias后，需要对IMU预积分进行重新计算。
代码见vins_estimator/initial/initial_aligment.cpp中的solveGyroscopeBias。

3.2 速度、重力和尺度初始化 (利用预积分约束估计$v_{b_k}^{b_k}$、$g^{c_0}$、$s$)

对于当前部分需要了估计的变量有：【论文式(16)】$${\mathcal{X}}_I^{3n+3+1}=[v_{b_0}^{b_0},v_{b_1}^{b_1},\cdots ,v_{b_n}^{b_n},g^{c_0},s]$$ 其中，$v_{b_k}^{b_k}$表示$k$时刻(捕获到图像的时刻)IMU body坐标系的速度在IMU body坐标系的表示，$g^{c_0}$为重力向量在第$0$帧相机坐标系下的表示，$s$表示尺度因子，将视觉轨迹拉伸到米制单位。

在IMU预积分中我们已经推导过基于世界坐标系$w$(东北天坐标系)的预积分量约束：$$R_w^{b_k}{p}_{b_{k+1}}^w=R_w^{b_k}(p_{b_k}^w+\underline{v_{b_k}^w}\Delta t_k-\frac{1}{2}{g}^w\Delta t_k^2)+{\alpha }_{b_{k+1}}^{b_k}$$ $$R_w^{b_k}\underline{v_{b_{k+1}}^w}=R_w^{b_k}(\underline{v_{b_k}^w}-g^w\Delta t_k)+{\beta }_{b_{k+1}}^{b_k}$$ 将世界坐标系$w$ 换成相机初始时刻坐标系$c_0$有： $${\alpha }_{b_{k+1}}^{b_k}=R_{c_0}^{b_k}(s({\bar{p}}_{b_{k+1}}^{c_0}-{\bar{p}}_{b_k}^{c_0})+\frac{1}{2}{g}^{c_0}\Delta t_k^2-\underline{R_{b_k}^{c_0}{v}_{b_k}^{b_k}}\Delta t_k)$$ $${\beta }_{b_{k+1}}^{b_k}=R_{c_0}^{b_k}(\underline{R_{b_{k+1}}^{c_0}{v}_{b_{k+1}}^{b_{k+1}}}-\underline{R_{b_k}^{c_0}{v}_{b_k}^{b_k}}+g^{c_0}\Delta t_k)$$
将论文式(14) (即本文公式(2)) 代入${\alpha }_{b_{k+1}}^{b_k}$有：$$\begin{gathered} \delta {\alpha }_{b_{k+1}}^{b_k}={\alpha }_{b_{k+1}}^{b_k}-R_{c_0}^{b_k}(s{\bar{p}}_{b_{k+1}}^{c_0}-s{\bar{p}}_{b_k}^{c_0}+\frac{1}{2}{g}^{c_0}\Delta t_k^2-R_{b_k}^{c_0}{v}_{b_k}^{b_k}\Delta t_k) \\ ={\alpha }_{b_{k+1}}^{b_k}-R_{c_0}^{b_k}(s{\bar{p}}_{c_{k+1}}^{c_0}-R_{b_{k+1}}^{c_0}{p}_c^b-(s{\bar{p}}_{c_k}^{c_0}-R_{b_k}^{c_0}{p}_c^b)+\frac{1}{2}{g}^{c_0}\Delta t_k^2-R_{b_k}^{c_0}{v}_{b_k}^{b_k}\Delta t_k) \\ ={\alpha }_{b_{k+1}}^{b_k}-s{R}_{c_0}^{b_k}({\bar{p}}_{c_{k+1}}^{c_0}-{\bar{p}}_{c_k}^{c_0})+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_c^b-p_c^b+v_{b_k}^{b_k}\Delta t_k-\frac{1}{2}{R}_{c_0}^{b_k}{g}^{c_0}\Delta t_k^2)=0_{3\times 1} \end{gathered}$$ 这里$v_{b_k}^{b_k}$、$g^{c_0}$和$s$均为待优化变量，将其转成$Ax=b$的形式：
$$R_{c_0}^{b_k}({\bar{p}}_{c_{k+1}}^{c_0}-{\bar{p}}_{c_k}^{c_0})s-v_{b_k}^{b_k}\Delta t_k+\frac{1}{2}{R}_{c_0}^{b_k}{g}^{c_0}\Delta t_k^2={\alpha }_{b_{k+1}}^{b_k}+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_c^b-p_c^b\text{\hspace{1em}(6)}$$ 对于${\beta }_{b_{k+1}}^{b_k}$, 则有 $$\delta {\beta }_{b_{k+1}}^{b_k}={\beta }_{b_{k+1}}^{b_k}-R_{c_0}^{b_k}(R_{b_{k+1}}^{c_0}{v}_{b_{k+1}}^{b_{k+1}}-R_{b_k}^{c_0}{v}_{b_k}^{b_k}+g^{c_0}\Delta t_k)=0_{3\times 1}$$ 这里的优化变量$v_{b_k}^{b_k}$、$v_{b_{k+1}}^{b_{k+1}}$、$g^{c_0}$，将其转成$Ax=b$的形式：
$$R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{v}_{b_{k+1}}^{b_{k+1}}-R_{c_0}^{b_k}{R}_{b_k}^{c_0}{v}_{b_k}^{b_k}+R_{c_0}^{b_k}{g}^{c_0}\Delta t_k={\beta }_{b_{k+1}}^{b_k}\text{\hspace{1em}(7)}$$ 将公式(6)(7)写出矩阵的形式：论文式【(18)(19)】
$$\begin{gathered} H_{b_{k+1}}^{b_k}{\mathcal{X}}_I+n_{b_{k+1}}^{b_k}={\left[\begin{array}{cccc}-I\Delta t_k& 0& \frac{1}{2}{R}_{c_0}^{b_k}\Delta t_k^2& R_{c_0}^{b_k}({\bar{p}}_{c_{k+1}}^{c_0}-{\bar{p}}_{c_k}^{c_0})\\ -I& R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}& R_{c_0}^{b_k}\Delta t_k& 0\end{array}\right]}_{6\times 10}{\left[\begin{array}{c}{v}_{b_k}^{b_k}\\ v_{b_{k+1}}^{b_{k+1}}\\ g^{c^0}\\ s\end{array}\right]}_{10\times 1}+n_{b_{k+1}}^{b_k} \\ ={\left[\begin{array}{c}{\alpha }_{b_{k+1}}^{b_k}+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_c^b-p_c^b\\ {\beta }_{b_{k+1}}^{b_k}\end{array}\right]}_{6\times 1}={\hat{z}}_{b_{k+1}}^{b_k}\text{\hspace{1em}(8)} \end{gathered}$$其中$R_{b_k}^{c_0}$、$R_{b_{k+1}}^{c_0}$、${\bar{p}}_{b_k}^{c_0}$、${\bar{p}}_{c_k}^{c_0}$可从视觉的SFM获得，$\Delta t_k$为相邻俩帧图像之间的时间间隔。
公式(8)转换成线性最小二乘问题对状态量进行求解：$$\underset{{\mathcal{X}}_{\mathcal{I}}}{\min }\sum _{k\in \mathcal{B}}||{\hat{z}}_{b_{k+1}}^{b_k}-H_{b_{k+1}}^{b_k}{\mathcal{X}}_I^k|{|}^2$$ 从矩阵角度来看，也看看做解方程 $H_{b_{k+1}}^{b_k}{\mathcal{X}}_I^k={\hat{z}}_{b_{k+1}}^{b_k}\to Ax=b$。
为了将矩阵系统化为矩阵利用LDLT求解，可得$H_{b_{k+1}}^{b_{k}T}{H}_{b_{k+1}}^{b_k}{\mathcal{X}}_I^k=H_{b_{k+1}}^{b_{k}T}{\hat{z}}_{b_{k+1}}^{b_k}\to Ax=b$，得到如下情况：

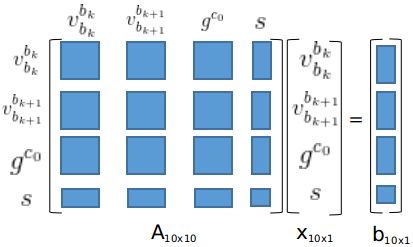
具体代码见 vins_estimator/initial/initial_aligment.cpp中的LinearAlignment().
在vins_mono代码中，由于具有多个$v_{b_k}^{bk}$需要优化，因此vins_mono将优化的变量均放在一个矩阵中，如下图所示：

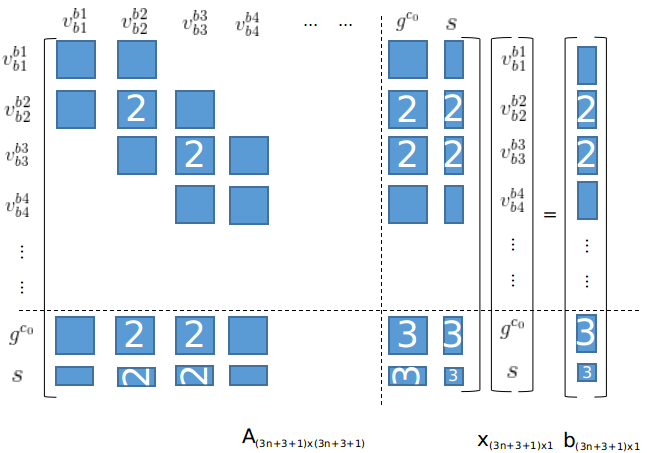
如上图所示考虑了将$(v_{b1}^{b1},v_{b2}^{b2},g^{c_0},s)$、$(v_{b2}^{b2},v_{b3}^{b3},g^{c_0},s)$、$(v_{b3}^{b3},v_{b4}^{b4},g^{c_0},s)$等三组变量构建的$Ax=b$放在了一个大矩阵中，其中蓝色框代表非零项，数字代表融合次数，未标数字代表1次融合。

3.3 优化重力向量$g^{c_0}$

为什么需要优化重力向量？
利用公式(8)求解的重力向量并没有模长的限制，即$||g^{c_0}||=9.81$，因此重力向量$g^{c_0}$实际上只有俩个自由度。

采用球面坐标，在切面空间上用两个变量重新参数化重力，将其表示为：$$\widehat{g^{c_0}}=||g||\cdot {\hat{\bar{g}}}^{c_0}+w_1{b}_1+w_2{b}_2=||g||\cdot {\hat{\bar{g}}}^{c_0}+bw$$ 其中${\hat{\bar{g}}}^{c_0}$为上一部分公式(8)得到的重力向量初始值的单位向量，$w_{2\times 1}=[w_1,w_2]$为待优化变量，$b_{3\times 2}=[b_1,b_2]$​中的$b_1,b_2$在$||g||\cdot {\hat{\bar{g}}}^{c_0}$的正切平面上且正交，定义如下：$$b_1=\{\begin{array}{c}({\hat{\bar{g}}}^{c_0}\times [1,0,0]),{\hat{\bar{g}}}^{c_0}\ne [1,0,0{]}^T\\ ({\hat{\bar{g}}}^{c_0}\times [0,0,1]),otherwise\end{array},b_2={\hat{\bar{g}}}^{c_0}\times b_1$$ 因此优化变量将从$g^{c_0}$(三个自由度)变为$w^{c_0}$(俩个自由度)：
$$\begin{gathered} H_{b_{k+1}}^{b_k}{\mathcal{X}}_I+n_{b_{k+1}}^{b_k}={\left[\begin{array}{cccc}-I\Delta t_k& 0& \frac{1}{2}{R}_{c_0}^{b_k}\Delta t_k^{2}b& R_{c_0}^{b_k}({\bar{p}}_{c_{k+1}}^{c_0}-{\bar{p}}_{c_k}^{c_0})\\ -I& R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}& R_{c_0}^{b_k}\Delta t_{k}b& 0\end{array}\right]}_{6\times 9}{\left[\begin{array}{c}{v}_{b_k}^{b_k}\\ v_{b_{k+1}}^{b_{k+1}}\\ w\\ s\end{array}\right]}_{9\times 1}+n_{b_{k+1}}^{b_k} \\ ={\left[\begin{array}{c}{\alpha }_{b_{k+1}}^{b_k}+R_{c_0}^{b_k}{R}_{b_{k+1}}^{c_0}{p}_c^b-p_c^b-\frac{1}{2}{R}_{c_0}^{b_k}\Delta t_k||g||\cdot {\hat{\bar{g}}}^{c_0}\\ {\beta }_{b_{k+1}}^{b_k}-R_{c_0}^{b_k}\Delta t_k||g||\cdot {\hat{\bar{g}}}^{c_0}\end{array}\right]}_{6\times 1}={\hat{z}}_{b_{k+1}}^{b_k}\text{\hspace{1em}(8)} \end{gathered}$$
采用最小二乘对待优化变量${\mathcal{X}}_I$进行重新优化。
具体代码见 vins_estimator/initial/initial_aligment.cpp中的RefineGrivity().
在代码中，当完成4次迭代完成$w_{2\times 1}=[w_1,w_2{]}^T$的求解后和$g^{c_0}$的每次更新，有${\hat{g}}^{c_0}=(g^{c_0}+[b_1,b_2]\ast [w_1,w_2{]}^T)$，则最后的重力向量为：$g^{c_0}＝\frac{{\hat{g}}^{c_0}}{||{\hat{g}}^{c_0}||}\ast ||g||$

3.4 对齐导航世界坐标系

由于我们的求解都是在第一帧相机坐标系$c^0$的，因此需要计算$R_{c_0}^w$将所有$c^0$坐标系下的变量转到世界坐标系下，令
$$R_{c_0}^w=exp([\theta \mathbf{a}])$$ 令${\hat{g}}^{c_0}$为重力细化后得到的$c^0$坐标系的重力向量，$g^w=[0,0,9.81{]}^T$为世界坐标系下的重力向量，故单位旋转轴$\mathbf{a}$为: $$\mathbf{a}=\frac{{\hat{g}}^{c_0}\times {\hat{g}}^w}{||{\hat{g}}^{c_0}\times {\hat{g}}^w||}$$ 旋转角度$\theta$为：$$\theta =atan\frac{{\hat{g}}^{c_0}\times {\hat{g}}^w}{{\hat{g}}^{c_0}\cdot {\hat{g}}^w}=atan\frac{||{\hat{g}}^{c_0}||\cdot ||{\hat{g}}^w||\sin \theta }{||{\hat{g}}^{c_0}||\cdot ||{\hat{g}}^w||\cos \theta }$$

问题1: 加速度的偏置$b_{at}$为什么没有估计？
由于线性加速度的模型为：${\hat{a}}_t=a_t+b_{at}+R_w^t{g}^w+n_a$，由于有重力的作用，加速度偏置$b_a$小$R_w^t{g}^w$几个数量级，很难在初始化的时候估计重力向量的同时估计出加速度偏置，故没必要初始化加速度偏置的初始值$b_{at}$

问题2：平移外参数$p_c^b$为何没有初始化？
由于平移相比于旋转而言，对于系统来�