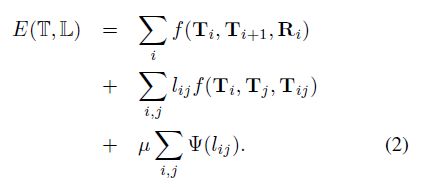qianyi-zhou offline RGB-D 三维重建（1）

读完zhou的这几篇论文，感觉他离线重建是在围绕一个思路在做，随着相机的移动，三维重建或者SLAM系统轨迹的累积误差会逐渐增大，SFM或者SLAM的后端优化，通常会有一个全局的优化，通过优化全部帧的位姿把求解的累积误差摊开，而zhou的思路不是这样的，zhou的思路是相机移动距离很大的时候累积误差会很大，但是当移动距离小的时候累积误差并不大，那好，我把整个图像序列划分成好多个小块，每个小块几十帧图像，划分的小快间会有重叠的图像。每个小块单独重建，小块内几十帧图像的重建累积误差会很小，重建完之后再根据每个小块重叠的部分将小块配准，计算小块间的位姿变换，再根据位姿变将小块融合到一起重建完整的三维模型。

先从最早的 13 年的文章说起，后面再介绍其它文章。
#"Dense Scene Reconstruction with Points of Interest"
这篇文章的思路是，对于输入的图像序列检测兴趣点，兴趣点是在扫描的时候重点关注的地方，如下图中重点扫描的地方是人的雕塑。然后根据检测出来的兴趣点，将整个图像序列划分成 $n$ 个fragments（这里将兴趣点周围划分的帧称为 fragment），这里 $n$ 既是兴趣点的个数，同时，还会划分得到连接前后 fragments 的 segments（将连接 fragments 的帧段称为 segment）。根据划分好的 fragments 和 segments，做 two pass 配准，第一次配准，对于每个 fragment 和 segment 都用现有的实时重建算法独立重建得到局部的模型，第二次配准，将每一帧图像和第一次重建得到的三维模型进行配准，得到位姿，第二次配准不生成三维模型，只是为了得到更加精确的位姿。两次配准后，对于 fragments 和 segments 之间进行回环检测，将由前面两次配准得到的前后帧位姿间约束，和回环检测形成的约束，放在一起做优化。优化的时候，fragments 内的约束作为硬约束，segments 内的约束作为软约束，这样在优化的时候会保持 fragments 内位姿求解基本不变，让 segments 帧去 absorb the residual error。

1、检测关键点
作者首先用现有的三维重建/SLAM算法对于序列图像进行配准，在序列图像中均与抽取一些 3D 点，根据配准计算得到的位姿，将3D点变换到同一个坐标系，变换到同一个坐标系后，根据3D点用RANSAC算法那抽取主平面，最后根据主平面上的点计算兴趣点，计算兴趣点用的是 mean shift 算法。

2、轨迹分割
计算得到兴趣点后，根据兴趣点将整个轨迹进行分割，分割的依据是如果帧和兴趣点比较相近，则将帧归为兴趣点所在的 fragments，分割还会得到的 fragments 之间的连接段 segments，既这些帧和所有的关键点都离得不近，轨迹分割用的是图割算法。

3、two pass 配准
前面说过，作者对每个 fragment 和 segment 进行两次独立配准，第一次配准对于每个 fragment 和 segment 会分别重建三维模型，第二次将每一帧和重建的三维模型再配准，得到的更加精确的位姿，第二次配准只是为了得到精确位姿，不重建三维模型。

4、全局位姿优化
作者对于没对 fragments 用 ICP 算法检测回环，并且将回环建立的约束和前面 two pass 配准前后帧之间的建立的约束放到一起，用 g2o 算法优化。优化的时候在同一个 fragments 内的约束作为硬约束（权值无穷大），其它约束作为软约束（前后帧约束设为单位权重，回环约束权重设为100）。通过这种方式，可以保持 fragments 内优化对于 pose 没影响（因为 fragments 内配准帧数少，累积误差本身就小，不用优化），优化改变 segments 帧间的 pose，segments 在重建时是不重要的区域。

5、融合重建
融合的时候同 KinectFusion 算法，博客地址（http://blog.csdn.net/fuxingyin/article/details/51417822）也是加权融合。不同的是由于 segments 和 fragments 会有重合，在融合 segments 帧时，这里会把 segments 部分的权值减小，这样来减弱 segments 和 fragments 重叠部分对于 fragments 重建影响。

再讲讲zhou另一个比较相关的工作
#“Robust Reconstruction of Indoor Scenes”
前面讲的那篇论文，过程有些复杂，这篇文章思路相对较简单。“Dense Scene Reconstruction with Points of Interest”思路是保证在兴趣点周围累计误差小，并且用全局的优化把各个 fragments 整合到一起。这篇文章的思路是直接将整个图像序列划分成等大小的小块，每个小块50帧图像，将这些小块独立进行重建，然后将重建好的小块两两配准，并且在小块间检测回环，由于检测出的回环准确率非常低，作者最后用优化的方式去掉错误的回环。

1、局部小块重建
作者将图像序列等大小划分成 fragments，每个 fragment 50 帧图像，然后将每个 fragment 单独重建，由于每个 fragment 帧数很少，从而基本没有累积误差。

2、geometric 配准
作者用三维特征将 fragments 两两进行配准，配准的目的是检测回环（两个 fragments 有重叠的部分），作者还做实验比较了当前几个三维特征配准算法，利用三维特征配准检测出的回环准确率是非常低的，小于20%。

3、robust 优化
这里优化的目的在于检测出来错误的回环，优化的目标函数如下：

公式里面 $T_i$ 和 $T_j$ 是每个fragments 相对于全局坐标系的位姿，$R_i$ 是通过三维重建或者SLAM算法计算得到 $P_i$ 和 $P_{i+1}$ 之间的位姿变换，$P_i$ 表示 fragment $i$，$T_{ij}$ 是回环检测得到的 $P_i$ 到 $P_j$ 间的位姿变换。

但是，这里优化的目的不是为了优化每个 fragments 的位姿 $T_i$，而是检测错误的回环，作者把优化的目标函数改成下面这样：

这个式子中优化项多了一项，$\Psi(l_(ij)) $ 表示 fragments $i$ 和 $j$ 是回环的确认程度，表达式为 $\Psi (l_{(}ij))=(\sqrt{l_{ij}}-1{)}^2$，这一项的含义是要尽量使得回环的条件成立（$l_{ij}\to 1$），尽可能多的检测出回环，当回环的条件不满足时，$f(T_i,T_j,T_{ij})$ 较大，也会使 $l_{ij}\to 0$。

$f(T_i,T_j,T_{ij})$ 是用来检测位姿 $T_i$，$T_j$ 和 位姿变换 $X$ 的不一致性，表达式如下：

上式中 $p$ 和 $q$ 是两个 fragment 中匹配的三维点，前面说到作者优化的目的不是为了求位姿 $T_i$，而是检测错误的回环，换句话说，就是使得错误回环的 fragments $l_{ij}$ 尽量小（$l_{ij}$ 表示 fragments $i$ 和 $j$ 是回环的 belief，值越大表示越相信 $i$ 和 $j$ 存在回环）。作者对于上式通过近似变换得到下面的目标函数：

$\xi$ 表示 6 个位姿参数。

通过对（2）式用 g2o 优化得到 $l_{ij}$ 的值，作者最后去掉 $l_{ij}<0.25$ 的回环项，认识这个地方是错误的回环。

作者实验验证通过这种方式可以将回环的准确率提高到 95% 以上，检测错误回环是作者这篇论文的核心工作。

版权声明：本文为博主原创文章，未经博主允许不得转载。