生成对抗树搜索的样本高效的深度强化学习
摘要
我们提出了一种样本高效的深度强化学习(DRL)算法——生成对抗树搜索(GATS)。在强化学习(RL)的搜索和规划中,尽管蒙特卡洛(MCTS)被认为是有效的,但其通常是样本低效的,从而应用到实践中成本高昂。在这项工作中,我们开发了一个用于对环境动力学建模的生成对抗网络(GAN)架构和奖励函数预测器模型。我们利用从与环境交互收集到的数据来学习这些模型,我们把这些模型用作基于模型的规划。在规划期间,我们部署了一个有限深度的MCTS,将已学好的模型用于树搜索和已学好的 Q Q 值用于叶节点, 以发现最好的动作。我们在理论上说明了GATS改善了基于值DRL中的偏置-方差权衡。此外,我们说明了相比于 Q Q 学习,该生成模型使用更少数量级的样本学到了模型动力学。在环境模型变化的非固定设置中,我们发现生成对抗模型比起 Q Q 学习适应新的环境要快得多。
1 介绍
最早的,宣传最好的深度强化学习(DRL)的应用包括Atari游戏和围棋棋盘游戏,由于环境是模拟的,所以其经验便宜。在这样的场景中,DRL会结合蒙特卡洛树搜索以用于规划,Agent在模拟的环境中(只要在计算上可行)执行roll-outs,以发现合适的策略。然而,对于一个情景问题,其每一个情节的长度都非常庞大,MCTS计算是非常昂贵的,比如围棋。为了加速围棋的蒙特卡洛树搜索(MCTS)和学习一种有效策略,Alpha Go在围棋模拟器上部署了一个更深但有限的MCTS,其中使用了一个学习好的 Q Q 函数来查询叶节点的值。
现实世界的应用中,比如机器人学,对话系统,采集样本通常会花费大量的时间和精力。着这样的场景中,Agent通常不能访问环境模型或者其对应的模拟器。由于海量样本复杂性,MCTS因而不能在这样场景中进行。在该工作中,受到Alpha Go的启发,我们提出了一种DRL算法,其利用环境样本来学习 Q Q 函数,还有用于构建一个MCTS可以进行的模拟器的环境动力学模型。有趣的是,在心理学领域,人们普遍认为,人类通过类似地想象未来和仔细考虑他们的决定来做出决策。
近来,生成对抗网络(GANs)作为生成模型的流行工具而出现,特别是在诸如图像等高维的数据中。和先前的由于要优化L1或者L2目标函数通常会产生模糊图像的图像生成方法不同的是,GANs生成清晰,真实的图像。GANs已经被扩展到用于条件生成,比如生成一幅以一个标签和视频预测为条件的图像。最近,作为一种新的GAN架构,提出了PIX2PIX,用于图像到图像的转换任务。
在该工作中,我们提出了生成对抗树搜索(GATS),一种利用了免模型和基于模型学习优势的样本高效DRL算法。我们构建了新的生成架构来学习动力学模型。对于基于模型的学习,在学习好的动力学模型和奖励过程上,我们开发了一个基于有界深度的MCTS算法,而对于免模型学习,我们使用了DQN和DDQN。特别地,GATS在特定深度上部署MCTS方法用于规划,并且为叶节点使用了一个估计的 Q Q 函数作为一个值。我们说明了使用我们新的架构,比起 Q Q 学习算法,该生成模型可以以更少的样本学到动力学模型。
生成动力学模型(GDM)和奖励预测器(RP)。 Atari游戏的拱廊学习环境中的状态包含图像(视频帧)。通过一个有条件的,基于先前帧和动作训练的以用于预测下一帧的GAN,该转移函数借助自身来近似。受到PIX2PIX的启发,我们为GDM开发了一个新的架构,用来学习模型动力学,和为RL生成后继状态。我们对GAN使用了Wasserstein度量,叫作W-GAN,并且我们使用了谱正则化技术创建一个稳定的和适应的GDM。在RL中,由于Agent遭遇非平稳数据分布,所以发现最好的架构,损失类,和GDM的优化模式是一个有挑战性的任务。我们对这些选择进行了广泛的研究,主要体现在附录中。RP是一个对给定状态和动作来预测期望的裁剪奖励的简单模型。在GDM训练期间,估计的Wasserstein距离低于频繁访问的状态-动作对,但高于罕见的看不见的状态-动作对。我们期待该距离会随着访问状态-动作对的数量的减少而增加。我们使用了这一表现为基于优化的探索-利用策略开发了一种启发式近似来代替 ϵ ϵ 贪婪策略。我们在经验上表明在GATS探索中的这种修改会带来更好的性能和样本复杂性。
在GATS期望的返回估计量中,我们理论上分析了估计误差的来源。我们研究了偏置-方差权衡,并且说明了DQN中的偏差项随着MCTS深度随方差增大而呈指数衰减。我们研究了DQN和DDQN的Q估计中的偏置,我们发现GATS即使向前一步(深度为1)也有助于解决偏置的夫负面影响。这就导致在Pong游戏中,DQN的样本复杂度降低了2倍。我们也发现进入更高的深度也不会为Pong带来更多的好处。在最新的ALE环境中,由于Pong的快速收敛和多游戏模式以及难度,我们选择该领域的Pong来作为我们的研究。 节省出来的计算时间允许我们做 Q Q 的偏置-方差的扩展研究——不同的基于模型的规划的影响,探索策略以及GDM的域转移。
最后,在该工作中,我们为最新的ALE环境开发了一个新的类OpenAI gym接口,其支持每一个游戏不同的模型和难度。为了研究在变化游戏动力学中的样本复杂性,我们在一个给定游戏的某种模式上训练了GDM和RP,并且我们改变了游戏的模式和难度。我们展示了比起GDM和RP以一小部分的样本适应新环境, Q Q 学习算法却需要采用更大量级的样本来适应。我们记载了并将在最新的ALE中开源该
2 相关工作
在RL的文献中,探索-利用权衡被广泛的研究。评估了MDPs的regret (这里没有找到合适的词来描述regret,所以先保留原词。)分析,其中面临不确定性(the Optimism in the Face of Uncertainty,OFU)的乐观主义被应用来确保一个高概率的regret上界。对于部分可观察的MDPs而言,OFU被证明具有很高的概率regret上界。此外,像部分监控的游戏等更一般的设置在理论上可以解决,并且提供了该问题在特定维度的极小极大的多项式依赖的regret保证。
尽管理论上理论上的RL解决了探索——利用的权衡,但该问题在经验的强化学习研究中仍然很严重。在经验方面,视频游戏最近取得的成功引发了一系列的研究兴趣。比如,[这些文献]([1,2,3])研究了对话策略学习的DRL,解决了探索的有效性问题。为了应对样本复杂性样本复杂性的缺点,设计一个DRL中的有效的探索策略已经作为一个活跃的研究课题出现了,比如乐观主义和Thompson采样。
使用 Q Q 函数的Bootstraps最小化Bellman残差已经是基于值得DRL方法得核心。提供一个值函数的偏置估计量来最小化Bellman残差被广泛的研究。为了减轻这种偏差以及其他原因,DQN提议不像模型的其他部分那样频繁地更新目标值,以便模拟Fitted- Q Q 的更新。这种调整减少了值估计量的偏差,但也显著地增加了样本复杂性。另一方方面,蒙特卡洛采样策略作为一种规划的有效方法被提出来,但是在现实世界的应用中遭遇了高样本复杂性。
最近,已经有了有条件的视频游戏的视频预测的研究,为了预测超长未来的给定动作的帧的轨迹,其庞大的模型用L2损失来训练的。生成帧的质量有训练在这些轨迹上DQN来度量。由于该模型使用了L2损失,在随机环境中或当帧包含高频模式时,它会产生合理的帧。另外,对于确定性的环境,我们实现该项工作并和GDM做了比较。我们观察到GDM需要明显更少的迭代来收敛到感知良好的帧,Q值(应用于真实帧和生成帧的Q函数)的偏差更小。
学习到的环境模型在[4]中被利用,其中使用编码器模型将生成的轨迹编码为抽象表示,其被用作策略模型的附加输入。他们在一个小型拼图世界验证了他们的方法。Sockoban进一步的展示了他们的模型在他们的miniPacman环境中多任务学习上的能力。[4]没有使用明确的规划和roll-outs策略。进一步的工作使用转换模型来在编码状态表示中执行roll-out,并且证明了在Atari游戏上的表现略有增加(相比于DQN)。相反地是,在本项工作中,我们在原始状态空间中学习到模型动力学,并且我们证明了在样本复杂性显著的经验性改进。
尽管GAN能够恢复输入数据流形并生成感知良好的图像,但它们很难训练并且通常不稳定,特别是对于像RL那样的非平稳任务。最近几年,在开发稳定的学习过程方面有了显著进步。虽然要求判别器是有界lipshitz函数的集合形式,但Wasserstein GAN(W-GAN)仍使用Wasserstein矩阵作为两个分布之间的距离慨念。为了满足这种有界性,提出了改良的W-GAN,其惩罚判别器梯度,但发现仍然难以训练。已经研究了判别器的谱正则化,其中经验地观察到了平滑的收敛。我们利用这些进展为GDM for RL创建稳定的学习程序。
3 基础
一个无限视野 γ γ -折扣的MDP——M是一个带有状态空间 X X ,行动空间 A A ,以及初始状态上的分布 P0 P 0 元组 <X,A,T,R,P0,γ> < X , A , T , R , P 0 , γ > 。转移核 T:x,a→Δx T : x , a → Δ x 和 [0,1] [ 0 , 1 ] 范围内的奖励 R:x,a→Δr R : x , a → Δ r 一起驱动着动力学模型, 0≤γ<1 0 ≤ γ < 1 。Agent的目标始要找到一个策略 π:=X→A π := X → A ,其能最大化期望的折扣奖励 η∗:=η(π∗)=maxπlimN→∞E[∑Nt=0γtrt|x0∼P0] η ∗ := η ( π ∗ ) = m a x π lim N → ∞ E [ ∑ t = 0 N γ t r t | x 0 ∼ P 0 ] 。令 Qπ(x,a):=limN→∞Eπ[∑Nt=0γtrt|x0=x,a0=a] Q π ( x , a ) := lim N → ∞ E π [ ∑ t = 0 N γ t r t | x 0 = x , a 0 = a ] 记为从状态——行动 x,a x , a 的策略 π π 下的平均折扣奖励。 为了发现在任何状态的最有行动,Agent可以学习Q函数。对于一个给定的状态和动作对 (x,a) ( x , a ) ,我们的目标实际上是最小化:
为了最小化上式目标式, 需要进行双采样来估计式子内的期望。为了避免双采样的成本,采用了一种最小化Bellman残差的通用方法来代替:
最小化该Bellman残差等价于最小化式子(1)和一个额外的附加项。DQN通过部署目标值的概念部分解决了这种偏置,
一般地,除了该偏置外,由于网络的有限能力,优化算法,模型失配,还有一个额外的统计量要考虑。在下一节,我们理论上和经验上研究该偏置,并且说明了GATS怎样解决这种不良的影响。对一个动态生成模型,我么提出了一个泛化的GDM,其包含一个生成器G和一个判别器D, 它们关于扩展了的有条件的Wasserstein度量进行对抗性训练。
这里的 z z 是一个0-均值,单位方差的高斯向量随机变量, ||⋅||L | | ⋅ | | L 指所有 Lipschitz−1 L i p s c h i t z − 1 函数的空间。在GDM中, D D 解决的是 sup s u p 的内部问题,而 G G 的目标是要最小化该距离,和学习所有 ϱ ϱ 的 Pϖ|ϱ P ϖ | ϱ 。我们在GATS上部署了我们提出的GDM,其中的 P P 是回放缓冲区中的 ϱ:(x,a) ϱ : ( x , a ) 对上的分布, Pϖ|ϱ P ϖ | ϱ 是在后继状态 ϖ:x′ ϖ : x ′ 上的分布,这就是转移核 T(x′|x,a) T ( x ′ | x , a ) 。
4 生成对抗树搜索
我们提出生成对抗树搜索(GATS)作为一个样本更高效的DRL算法。构建在DQN和DDQN上的GATS,通过复用回放缓冲区的经验来学习一个奖励模型RP和动力学模型GDM。然后,GATS在已学好的模型(GDM和RP)部署了有限深度的蒙特卡洛树搜索来代替实际环境中的规划。随后,其使用了一个已学好的 Q Q 函数来估计叶节点处的最大期望回报,如图6。为了学到模型动力学,我们提出了由 θGDM θ G D M 参数化的GDM,作为PIX2PIX(PIX2PIX是一个图像到图像的转换模型)架构的扩展。GDM的输入是状态(四幅连续帧)和一系列动作,GDM从其中生成后续帧。我们通过从回放缓冲区中采样小批量的经验来训练GDM。与此同时,我们使用来自回放缓冲区的样本来训练由 θRP θ R P 参数化的RP。
偏置和方差权衡。在前一节中,我们DQN中使用到的目标函数。等式(2)本质上是一个有偏估计量。在接下来一节, 我们说明了实践中的这些偏差有多大。另外,除了DQN和统计偏差,由于定义在DQN中的序列回归中的低采样机制,已学过的Q会产生方差。令 eQ e Q 记为 Q Q 函数中估计误差的上界; |Q(x,a)−Q~(x,a)|≤eQ | Q ( x , a ) − Q ~ ( x , a ) | ≤ e Q , ∀x,a ∀ x , a ,其中 Q~(x,a)=E[r+maxa′Q(x′,a′)] Q ~ ( x , a ) = E [ r + m a x a ′ Q ( x ′ , a ′ ) ] 。对于一个给定的,使用了GDM,RP,和估计的Q的roll-out策略 πr π r ,期望回报 ξp(πr,x) ξ p ( π r , x ) (下标 p p 代表预测)为:
因为该期望不是在真实的环境中,给定GDM,RP和Q估计,GATS有效地估计了该期望回报,而不需要与真实环境交互。令 ξ(πr,x) ξ ( π r , x ) 记为真实模型下的相同量:
此外,对于RP和GDM,这里的 T^ T ^ 是估计转移核, ∀x,x′,x^,x^′,a∈X,A ∀ x , x ′ , x ^ , x ^ ′ , a ∈ X , A :
定理1。[偏置—方差权衡]如果运行GATS以使用DQN程序与来自GDM和RP的学习环境模型估算 Q Q 函数,那么在估计 ξp(πr,x) ξ p ( π r , x ) 中的偏差对 ∀x ∀ x 和 πr π r 是有界的:
证明。我们分解了估计量 ξp(πr,x) ξ p ( π r , x ) (等式(4)的右边项)中的误差。 ξp(πr,x) ξ p ( π r , x ) (等式(4)的右边项)的估计中的第一项带有建模环境中一个误差,其取决于RP和GDM模型的不足,第二部分是主要是由于 Q Q 函数的DQN估计中的偏置和方差引起的 eQ e Q ,还有由于在 x^H x ^ H 中的分布转移的GDM。因此,对于第二项,通过增加和减去该项—— Eπr[γHmaxaQ~(x~H,a)] E π r [ γ H max a Q ~ ( x ~ H , a ) ] ,我们有:
11−γ 1 1 − γ 这一项的出现是因为最大可能 Q Q 不大于 11−γ 1 1 − γ 。要限界 P(xH|x,πr)−P^(x^H|x,πr) P ( x H | x , π r ) − P ^ ( x ^ H | x , π r ) ,我们需要进一步对他们进行扩展。比如,对 P(xH|x,πr) P ( x H | x , π r ) ,我们有:
又,使用加和减的技巧,该差可以写成:
因为 eT e T 是转移核估计的界;
现在,我们可以解释GATS在 Q Q 估计中可以显著(以深度指数地)减少偏置核方差,记为 γHeQ γ H e Q 。同时,由于最大可能 Q Q 小于等于 11−γ 1 1 − γ , 由GDM产生的等式(6)中的第二项误差减为 γH1−γHeT γ H 1 − γ H e T 。估计量 ξp(πr.x) ξ p ( π r . x ) 的另一个误差来源是等式4中的右边的第一项。其是由于RP和GDM模型缺陷所致。
为了约束该量,我们使用了相同的分解过程;
定理1提供了每个误差来源对GATS预测期望回报 ξp(πr,x) ξ p ( π r , x ) 的贡献的洞察。Q估计中的指数消失误差是以模型估计中的变化为代价的。因此,Agent选择了roll-out的深度H,以这种方式来最小该估计量误差。
5 实验
我们在一个类似Atari的游戏,使用了OpenAI Gym的Pong扩展研究了GATS的性能。DQN架构和游戏设计选择都充分借鉴了[5]。受PIX2PIX网络的启发,GDM的架构扩展了用于生成器的已提出的U-Net模型。该GDM接收一个状态,系列动作和高斯噪音,输出下一个状态。RP是一个带有3个输出的简单模型,每个输出对应一个可能的限幅奖励。我们我们使用加权(相近样本有更高权重)的大小为128的小批量数据来训练GDM和RP,并每隔16GATS的决策步就更新两个网络(比Q的更新频率低4倍),我们在已学好的模型上部署GATS作为限界深度的蒙特卡洛树搜索,并且在叶节点使用了已学好的Q值。
Qθ Q θ 的偏差—方差。为了观察既有的偏差和方差。我们在游戏—Pong上单独运行了20M时间步DQN。图1展示了4个连续帧,Agent在这4个连续帧中接收到一个负分。在时间步 t t 的表1展示由DQN对这些步估计的Q值。正如我们在图1和表1中看到的,在时间步 t t ,所有动作的估计Q值大都一样。该Agent采取向下的动作,环境进入到下一个 t+1 t + 1 状态
.表1的第二行表明了这些动作在新的状态下的Q值。由于该转移不携带任何奖励,并且折扣因子接近1( γ=0.99 γ = 0.99 ),所以我们期望时间步 t+1 t + 1 的最大 Q Q 值接近向下动作的 Q Q 值,但是其非常不一样。
此外,在图2和表2中,我们探讨了Agent捕捉球的情况。这个球将会向右走,Agent需要捕捉到它。在时间步 t t ,球拍不在球的速度方向上,如表2所示。最优的动作是向下。但仔细观察动作的估计Q值可以发现,两种动作的Q值都不合理地接近,这可能导致失分。最后,我们研究了使用DQN的Q函数估计中既有的的误差。在表1中,如果Agent在做出决策之前可以roll-out一步,它可以观察到向下动作的负面结果。roll-out的积极影响在 Q Q 学习的早期更显著,此时的Q估计更大。
我们向前地运行了1,2,3和4步的GATS(GATS1,GATS2,GATS3,GATS4),并且在图3中(左)展示了其在DQN上性能的改善。图3(右)展示了RP预测准确率。我们观察到:当转移出现在时间步1M时,RP模型对正向奖励分错了类。但是RP快速地适应了这种转移,并且减少分类错误到每个情节2个错误。图5展示了GDM仅通过作用在第一帧上的条件以及动作轨迹就可以生成接下来9帧是有多准确。该轨迹是在决策步100k时产生的。除了DQN上的GATS, 我们也在DDQN上进行了系列实验。
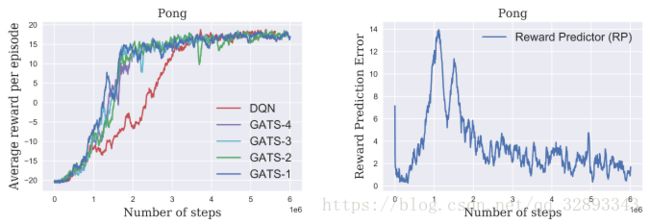
图3 左:比起原始DQN,GATS能更快(快2倍)地学到一个更好的策略。GATS k k 记为深度为 k k 的GATS。右:RP的准确率。Y轴时每个情节犯错数,每个情节的平均长度为2k,因此该准确率几乎总是在 99.8% 99.8 % 附近。该准确率在多轮runs中和不同的向前看的长度中是一致的。
图3展示了除一步以外的更深的roll-out并没有向Pong提供额外的好处,因此我们聚集接下来两个实验的一步roll-out。在第一个实验中, 我们为GATS提出了一个新的基于乐观主义的探索。Wassertein度量的一个有趣特性是这种距离随着频繁看到的状态—动作经历而减小,并对罕见的经历保持较大值。直观地,对于不相似的经历, 生成器不能生成一幅合适的帧来糊弄判别器, 因此Wasserstein距离值很大。我们可以使用该距离作为这些经历上的一个逆伪数(也叫有限态MDP计数)下降函数的一个近似, 也就是 1N~(x,a) 1 N ~ ( x , a ) 。由于其在上置信界RL(Upper Confidence bound RL, UCRL)—一个基于MDPs分析的OFU, 因此我们可以使用这个伪计数来近似学习Q函数的乐观度。乐观的 Q,Q~ Q , Q ~ 如下:
其中 T T 是水平时间, c c 是置信度标准常数。我们可以解耦 Q Q 学习和置信学习部分中的等式(7),即: Q~π(x,a)=Qπ(x,a)+Cπ(x,a) Q ~ π ( x , a ) = Q π ( x , a ) + C π ( x , a )
因此,我们可以使用DDQN学习 Q Q 一样的方式来学习 C C 。由于我们无法访问计数,也无法进行 Q Q 学习,所以,受启发地, 我们用在 (x,a) ( x , a ) 处缩放的Wasserstein距离来代替 clog(T)N~(x,a)−−−−−√ c log ( T ) N ~ ( x , a ) 和近似 C C 函数。因此,我们部署了学到的置信度,并将他添加到我们的GATS算法的 ξ(πr,x) ξ ( π r , x ) 中,即: maxπξ~(πr,x)+C(πr,x) max π ξ ~ ( π r , x ) + C ( π r , x ) 。这种启发式的方法鼓励Agent探索GDM表现不好部分的状态空间。如果这部分状态空间对应低频访问的状态空间部分,那么相对于 ϵ ϵ 贪婪策略更有助于探索。
在第二个实验中,我们研究了新近训练样本对GDM的优先级的影响,我们在图4(左)中报告的所有实验中都这样做。我们研究了从图4(右)的回放缓冲去中随机均匀地选择GDM输入样本的情况。在这种情况下,GATS比起游戏的一开始更快地学习到了有一个更好的策略,但由于状态分布的转移,其性能次于DDQN。值得注意的是,没有 ϵ ϵ 贪婪策略而基于乐观主义的探索是其接近最大分数21的原因。我们用 ϵ=0 ϵ = 0 训练了DDQN和GATS-DDQN,并且他们的性能都接近21。
6 讨论
GATS算法的一个新的方面使其灵活性。GATS包含几个构建快: (i) ( i ) 值学习;我们部署了DQN和DDQN, (ii) ( i i ) 规划;我们使用了纯粹的蒙特卡洛采样, (iii) ( i i i ) 奖励预测器;我们使用了简单的3—分类器; (iv) ( i v ) 模型动力学,我们提出了GDM架构。实际上,可以轻松地为每个这些块部署任何其他方法。举个例子,对于值学习 (i) ( i ) ,可以使用基于值的方法。对于规划 (ii) ( i i ) ,可以使用上置信界树搜索(UTC)或者策略梯度方法。对于奖励模型 (iii) ( i i i ) ,如果奖励是一个连续分布,可以使用任何回归模型来学习该均值奖励。最后对于模型动力学 (iv) ( i v ) ,可以扩展GDM或者选择其他任何图形生成模型。有趣的是,该项工作可以扩展到 λ λ —设置,其中获得了 n n 步混合。GATS设计中的这种自由允许很容易适应不容领域和问题,并且提供了进一步探索的诸多路劲。尽管GATS提供的许多优势是一个灵活的RL范式,但其由于MCTS而受到计算成本的影响。可以通过并行化或通过一个更小的网络蒸馏策略方法放宽此开销,不过这不在该工作中聚集。
7 致谢
参考文献
笔者注: 引用的这部分参看文献是为了体现文章翻译的完整性,并没有将所有文章所涉及到的文献都列举出来,主要是为了避免文章赘余。这里向没有被列举出来的文献的作者表示歉意,但读者们仍然可以通过原文查找到相关参考文献的原作者。
[1] H. Cuayáhuitl. Simpleds: A simple deep reinforcement learning dialogue system. arXiv:1601.04574, 2016.
[2] M. Fatemi, L. E. Asri, H. Schulz, J. He, and K. Suleman. Policy networks with two-stage training for dialogueh systems. arXiv:1606.03152, 2016.
[3] T.-H. Wen, M. Gasic, N. Mrksic, L. M. Rojas-Barahona, P.-H. Su, S. Ultes, D. Vandyke, and S. Young. A network-based end-to-end trainable task-oriented dialogue system. arXiv:1604.04562, 2016.11
[4] T. Weber, S. Racanière, D. P. Reichert, L. Buesing, A. Guez, D. J. Rezende, A. P. Badia, O. Vinyals, N. Heess, Y. Li, et al. Imagination-augmented agents for deep reinforcement learning. arXiv, 2017.
[5] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, et al. Human-level control through deep reinforcement
learning. Nature, 2015.
Appendix
笔者注: 附录部分是对正文中提到一些模型和方法的细节的具体描述,这里不再仔细翻译此部分。读者可以参考原文了解更多细节。
论文原文
Sample-Efficient Deep RL with Generative Adversarial Tree Search




