1327G - Letters and Question Marks(AC自动机+状压DP)

题目链接

题目大意：

给$k$个字符串$t_1,t_2,...t_k$，$t_i$有权值$c_i$.令$F(T,t)$表示字符串$T$中包含多少个$t$，$G(T)={\sum }_{i=1}^{k}F(T,t_i)\ast c_i$。
现在给出一个字符串$S$,$S$中有最多14个位置是未知的，你可以在这些位置上填互不相同的字母$a-n$，求$G(S)$最大可以是多少。
$\sum |t_i|\le 1000,|S|\le 5e4,-10^6\le c_i\le 10^6$

解题思路

注意到未知的位置较少，且必须要填互不相同的字母，这提示我们用状压DP去写。
而统计一些模板字符在一个字符串里面出现的次数和贡献，可以使用ac自动机求出。在这题中的障碍是那些未知的位置。
注意到$\sum |t_i|\le 1000$，AC自动机最多有1000个结点。未知位置最多有14个，所以原本的串$S$最多被分成15段已知的固定的串。
我们令$nxt[u][i]$表示ac自动机的结点$u$跑一遍$S$的第$i$段串之后变成了结点$nxt[u][i]$。令$sum[u][i]$表示这个过程中得到的贡献。
我们用$dp[u][mask]，(假设mask中的1的个数为cnt)$表示：
处理完前$cnt$个未知位置，使用的字符集合为$mask$，当前位置为第$cnt+1$段的最后一个字母，在ac自动机上的位置为结点$u$的情况下，得到的G的最大值.
它的转移如图表示：

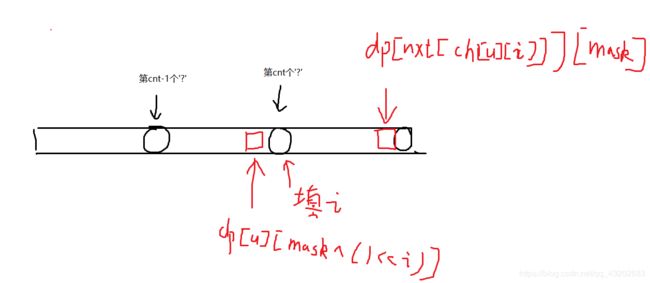
先枚举当前使用的字符集合mask，然后枚举上一段的结尾走到了ac自动机的u，根据第cnt个位置填什么字符来转移：
转移的时候有三段贡献：

1. 前面的dp值
2. 从上一段最后一个位置走到第cnt个’?’(填了i)得到的贡献
3. 走到cnt+1段的最后一个位置的贡献

dp[ nxt[ch[u][i]][num] ][mask] =max(dp[ nxt[ch[u][i]][num] ][mask], dp[u][mask^(1<<i)]+cost[ch[u][i]]+sum[ch[u][i]][num]);

ac代码：

#include
#define ll long long
#define lowbit(x) ((x)&(-(x)))
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
using namespace std;
const int maxn = 4e5 + 50;
int ch[maxn][15], fail[maxn];
ll cost[maxn], rt, tot = 0;
void ins(char *s, int val){
    int p = rt;
    while(*s){
        int x = *s - 'a';
        if(!ch[p][x]) {
            ch[p][x] = ++tot;
        }
        p = ch[p][x];
        s++;
    }
    cost[p] += val;
}
queue<int> q;
void get_fail()
{
    while(q.size()) q.pop();
    for(int i = 0; i < 15; ++i)
        if(ch[rt][i]) q.push(ch[rt][i]), fail[ch[rt][i]] = rt;
        else ch[rt][i] = rt;
    while(q.size()){
        int cur = q.front(); q.pop();
        for(int i = 0; i < 15; ++i){
            if(ch[cur][i]) {
                fail[ ch[cur][i] ] = ch[ fail[cur] ][i];
                q.push(ch[cur][i]);
                cost[ch[cur][i]] += cost[ fail[ ch[cur][i] ] ];
            }
            else ch[cur][i] = ch[fail[cur]][i];
        }
    }
}
char t[1050];
void init(){
    tot = 0; rt = ++tot;
    int n; scanf("%d", &n);
    fors(i, 0, n){
        int x;
        scanf("%s%d", t, &x); ins(t, x);
    }
    get_fail();
}
char s[maxn];
int pos[20], cnt = 0;
int nxt[1050][17];
ll sum[1050][17];
ll dp[1050][1<<14];
int cal(int x){int res = 0; while(x) res++, x-=lowbit(x); return res;}
void sol(){
    scanf("%s", s);
    int n = strlen(s);
    pos[cnt++] = -1;
    fors(i, 0, n) if(s[i] == '?') pos[cnt++] = i;
    pos[cnt] = n;
    fors(i, 0, cnt){
        fors(u, 1, tot+1){
            int p = u;
            fors(j, pos[i]+1, pos[i+1]){
                p = ch[p][s[j]-'a'];
                sum[u][i] += cost[p];
            }nxt[u][i] = p;
        }
    }
    memset(dp, 0xcf, sizeof dp);
    dp[nxt[rt][0]][0] = sum[rt][0];
    ll ans = -1e18;
    if(cnt == 1) ans = sum[rt][0];//if there is no "?"
    fors(mask, 1, (1<<14)){
        int num = cal(mask);
        if(num > cnt-1) continue;
        fors(u, 1, tot+1){
            fors(i, 0, 14){
                if(mask>>i&1){
                    dp[ nxt[ch[u][i]][num] ][mask] =
                    max(dp[ nxt[ch[u][i]][num] ][mask], dp[u][mask^(1<<i)]+cost[ch[u][i]]+sum[ch[u][i]][num]);
                    if(num == cnt-1) {
                        ans = max(ans, dp[ nxt[ch[u][i]][num] ][mask]);
                    }
                }
            }
        }
    }
    cout<<ans<<endl;
}
int main()
{
    init();
    sol();
}