广东省强网杯逆向题 SimpleGame writeup

在i春秋平台上找到的这题，200分的题就是不一样哈：）
地址：reverse 题目SimpleGame
先运行一下，看起来还挺简单的（然而虐了我好长时间），输入flag，然后给出结果。加载到ida，一上来发现有壳。然后就查了下壳：upx

脱壳一开始用的esp定律，因为在程序开头发现一个pusha，然后alt+t搜索popa

跟进到jmp目的地址发现应该还不是oep，继续跟进 直到一个call指令 f7单步步入到了401400

应该是oep无疑了（ps：在分析的时候会发现这个程序用了security cookie的保护形式，是因为当读入flag的时候没有做字符数限制，可以触发栈溢出，当然这和这道题并无啥卵关系）
oep找到了，那就来脱壳吧
这里我用pe tools来dump的，importREConstructor来修复IAT，大家可以在52破解上找到资源

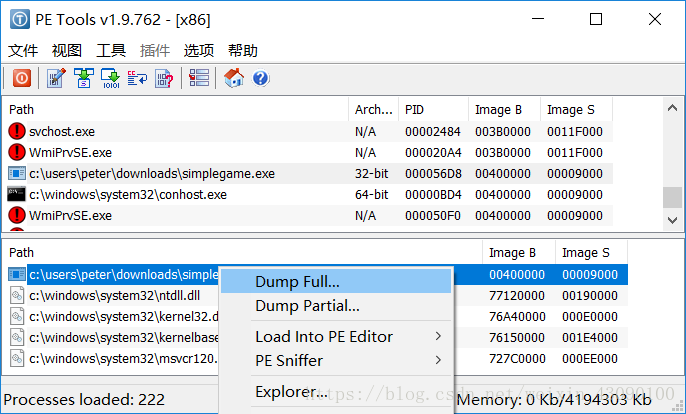
在401400往下拉一些就能找到一个printf函数的call


这里跟到esi的地址，找到IAT

起始地址，终止地址我都用粉色标了出来，然后就是importREConstructor

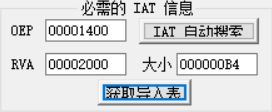
然后最终修复文件是dumped_.exe

---

接下来就是愉快的逆向分析

注意一下粉色标出来的地方本来是 jnz，但是如果这样的话直接运行就中断了，所以在这里打了一个补丁，修改成了jmp。
下面开始真分析
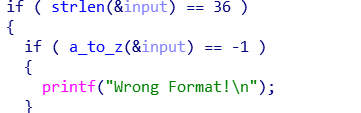长度是36，输入的字符必须是小写字母。

---

这里有三个检查函数，分别看一下
你会发现第一个函数代码量远远大于第二三个，所以就先从第一个函数开始

---

---

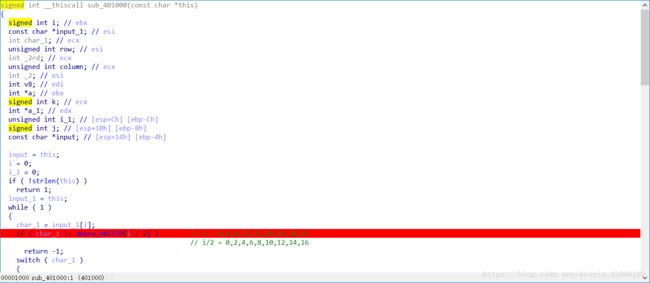
这里我分别用_0 、_1代表四个字符中第0个和第1个，以此类推。 403170地址上如果在动态调试之前是这样的

显然不对，动态调试到断点，在跟到403170地址上，dump下来的数组是这样的

所以可以知道 list_0 = ‘dswswwawd’，list_2=’sdaaaasdw’。
下面是个switch语句： _0 = ‘a’, _0=’d’情况如下

在这种情况下，_2只能是s或者w
再往下翻一些是_0 = ‘s’, _0=’w’情况，可以和上面相类比：

这里我定义了两个变量，row和column，这么命名是有原因的，现在还不能看出来row和column的意义，但是知道row和column与_1和_3相关。

粉色标出来的地方均可表明又是恶心的二维数组， 相对应的命名了两个二维矩阵。可以根据循环次数推出matrix_A其实是9个4*4的二维数组， 跟进到matrix_B地址可以发现其是一个9*9的二维数组。分别将A和B从hex-view里抠出来，这里就不放图了。在最底下的解题脚本里会给出生成矩阵的代码
A:
0090
0990
0090
0000

0600
0600
0600
0600

0000
0300
3300
3000

0080
0080
0880
0000
…………
B:

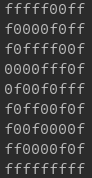
这里的代码逻辑可以这么思考A和B是0的位置就相当于一个空格，非0就是有东西。将A中的第i个小矩阵嵌入B矩阵中，以（row，column）坐标为起点4*4的小矩阵中，如果有任何一个重合位置两个小矩阵都有东西，就return -1。也就是说所有重叠位置均只能有至多一个东西不能有两个东西。然后还要将A中第i个小矩阵嵌入到B矩阵中，下一次判断的B矩阵就是第i个小矩阵嵌入后的矩阵。
e.g.
拿A中第一个小矩阵为例，将其嵌入到B矩阵
B:

A:
0090
0990
0090
0000
有三个坐标可以实现不重叠嵌入，分别是(4, 3), (5, 3), (5, 5) 【ps:坐标形式是 (row，column)】
不妨试一试
但我们知道答案应该是唯一的，但第一步这就出现了三种情况怎么办，这时候需要解题脚本一个dfs函数，搜索出能使A的9个小矩阵都能嵌入到B中的情况。
前面写过每一个row和column都是由_1和_3生成的，生成规则很简单无非就是加减法，这里并不是难点。所以从row和column倒推出_1和_3也是很容易。
总结一下我们的解题脚本需要的功能：
1、由ida中dump出来的数据生成矩阵A和矩阵B
2、用深搜+回溯实现矩阵A嵌入到矩阵B，记录被嵌入的B中4*4小矩阵的起点坐标(row，column)
3、一直每个起点坐标，反向推出每个_1和_3

---

以下是我写的py脚本，代码量比较大，建议分片来看

ans = []

def dfs(step):
    if step == 9:
        print(ans)
    else:
        pos = []
        for row in range(6):
            for column in range(6):
                sum = 0
                for i in range(4):
                    for j in range(4):
                        if a[16 * step + 4 * i + j]:
                            if b[9 * (i + row) + j + column]:
                                break
                        sum += 1
                if sum == 16:
                    pos.append((row, column))
        for position in pos:
            for i in range(4):
                for j in range(4):
                    if a[16 * step + 4 * i + j]:
                        b[9 * (i + position[0]) + j + position[1]] = a[16 * step + 4 * i + j]
            ans.append(position)
            dfs(step+1)
            for i in range(4):
                for j in range(4):
                    if a[16 * step + 4 * i + j]:
                        b[9 * (i + position[0]) + j + position[1]] = 0
            del ans[step]


A = '''00 00 00 00 00 00 00 00  09 00 00 00 00 00 00 00
00 00 00 00 09 00 00 00  09 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  09 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 06 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 06 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 06 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 06 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 03 00 00 00  00 00 00 00 00 00 00 00
03 00 00 00 03 00 00 00  00 00 00 00 00 00 00 00
03 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  08 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  08 00 00 00 00 00 00 00
00 00 00 00 08 00 00 00  08 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 05 00 00 00  05 00 00 00 00 00 00 00
00 00 00 00 05 00 00 00  05 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
02 00 00 00 02 00 00 00  02 00 00 00 02 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 07 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 07 00 00 00  07 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  07 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  04 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  04 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 01 00 00 00  01 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  01 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  01 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00'''
B = '''0F 00 00 00 0F 00 00 00  0F 00 00 00 0F 00 00 00
0F 00 00 00 00 00 00 00  00 00 00 00 0F 00 00 00
0F 00 00 00 0F 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  0F 00 00 00 00 00 00 00
0F 00 00 00 0F 00 00 00  0F 00 00 00 00 00 00 00
0F 00 00 00 0F 00 00 00  0F 00 00 00 0F 00 00 00
00 00 00 00 00 00 00 00  0F 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  00 00 00 00 0F 00 00 00
0F 00 00 00 0F 00 00 00  00 00 00 00 0F 00 00 00
00 00 00 00 0F 00 00 00  00 00 00 00 00 00 00 00
0F 00 00 00 00 00 00 00  0F 00 00 00 0F 00 00 00
0F 00 00 00 0F 00 00 00  00 00 00 00 0F 00 00 00
0F 00 00 00 00 00 00 00  00 00 00 00 0F 00 00 00
00 00 00 00 0F 00 00 00  0F 00 00 00 00 00 00 00
00 00 00 00 0F 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00  0F 00 00 00 0F 00 00 00
0F 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00
00 00 00 00 0F 00 00 00  00 00 00 00 0F 00 00 00
0F 00 00 00 0F 00 00 00  0F 00 00 00 0F 00 00 00
0F 00 00 00 0F 00 00 00  0F 00 00 00 0F 00 00 00
0F 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00'''
#  ---------------------------------------init----------------------------------------
a = A.split('\n')
b = B.split('\n')
a_1 = []
b_1 = []
for i in range(len(a)):
    temp = a[i].split('  ')
    a_1 += temp[0].split(' ')+temp[1].split(' ')
for i in range(len(b)):
    temp = b[i].split('  ')
    b_1 += temp[0].split(' ') + temp[1].split(' ')
print(a_1, b_1)
a = []
b = []
for i in range(0, len(a_1), 4):
    a.append(int(a_1[i]))
for i in range(0, len(b_1), 4):
    b.append(eval('0x'+b_1[i]))
#  -----------------------------------------------------------------------------------
'''print('\n\n', a, b, sep='\n')'''
#  -------------------------------------generate_matrix-------------------------------
for i in range(9):
    for j in range(4):
        for k in range(4):
            print(a[16*i+4*j+k], end='')
        print('\n', end='')
    print('\n', end='')
for row in range(9):
    for column in range(9):
        if b[9*row+column] == 15:
            print('f', end='')
        else:
            print(b[9*row+column], end='')
    print('\n', end='')
#  ------------------------------------------------------------------------------------
order = [9, 6, 3, 8, 5, 2, 7, 4, 1]
dfs(0)
ans = [(5, 5, 9), (4, 4, 6), (1, 0, 3), (5, 2, 8), (2, 1, 5), (0, 1, 2), (5, 0, 7), (1, 5, 4), (0, 4, 1)]
_0 = 'dswswwawd'
_1 = []
_2 = 'sdaaaasdw'
_3 = []
row = 0
column = 1
for i in range(len(_0)):
    input_1 = -1
    input_3 = -1
    if _0[i] == 'a':
        input_1 = chr(100-ans[i][column])
    if _0[i] == 'd':
        input_1 = chr(ans[i][column]+94)
    if _0[i] == 's':
        input_1 = chr(ans[i][row]+95)
    if _0[i] == 'w':
        input_1 = chr(99-ans[i][row])
    _1.append(input_1)
    if _0[i] == 'a' or _0[i] == 'd':
        if _2[i] == 's':
            input_3 = chr(ans[i][row]+95)
        if _2[i] == 'w':
            input_3 = chr(99-ans[i][row])
    else:
        if _2[i] == 'a':
            input_3 = chr(100-ans[i][column])
        if _2[i] == 'd':
            input_3 = chr(ans[i][column]+94)
    _3.append(input_3)
for i in range(len(_0)):
    print(_0[i]+_1[i]+_2[i]+_3[i], end='')
#  input='dcsdscdbwbadsdabwaacwcacadsdwbdcdbwc'

最后的flag别忘加上flag{}
flag：flag{dcsdscdbwbadsdabwaacwcacadsdwbdcdbwc}

---

在脱壳的时候我用的是ida脱的壳，因为在用ollydbg的时候pause在了奇怪的地方
call edx；edx的地址超出所有的段
但是ida却没有这个情况，是不是大家在做这个题的时候也遇到了这种情况，所以还想请教一下大神们这是什么原因，如果可以的话希望可以有评论