机器学习 【决策树ID3算法/C4.5算法/CART算法+随机森林算法】 公式推导计算+详细过程 (入门必备)
- 决策树可用于分类和预测。常见的决策树算法有ID3、C4.5和CART。
- 信息熵:不确定性的度量,事物越混乱就越不确定,信息熵越小越事物越确定。
- 信息增益:信息增益越大,事物的不确定性下降的越快,也就是说事物越趋近于确定,信息增益越大不确定性下降越快。
- 信息增益率:信息增益率越大,事物越确定。
- 基尼系数:不确定性的度量,事物越混乱就越不确定,基尼系数越小越事物越确定。
信息熵公式
E n t r o p y ( D ) = − ∑ i = 1 m p i l o g 2 p i Entropy(D) = -\sum_{i=1} ^ m p_i log_{2}p_i Entropy(D)=−i=1∑mpilog2pi
上式中 p i p_i pi为 i i i类样本所占比例。
- ID3:使用信息增益作为划分属性的依据。
信息增益公式
G a i n ( D , A ) = E n t r o p y ( D ) − ∑ i = 1 m D m D E n t r o p y ( D m ) Gain(D, A) = Entropy(D) - \sum_{i=1} ^ m \frac{D_m}{D} Entropy(D_m) Gain(D,A)=Entropy(D)−i=1∑mDDmEntropy(Dm)
上式中 D m D \frac{D_m}{D} DDm为第m个划分节点的权重值。
- C4.5:使用信息增益率作为划分属性的依据。
信息增益率公式
G a i n R a t i o ( D , A ) = G a i n ( D , A ) E n t r o p y ( D ) GainRatio(D, A) = \frac{Gain(D, A)}{Entropy(D)} GainRatio(D,A)=Entropy(D)Gain(D,A)
上式中
E n t r o p y ( D ) = − ∑ i = 1 m ∣ D m ∣ ∣ D ∣ l o g 2 ∣ D m ∣ ∣ D ∣ Entropy(D) = - \sum_{i=1} ^ m \frac{|D_m|}{|D|} log_{2} \frac{|D_m|}{|D|} Entropy(D)=−i=1∑m∣D∣∣Dm∣log2∣D∣∣Dm∣
- CART:使用基尼系数作为划分属性的依据。
基尼系数公式
推导:
E n t r o p y ( D ) = − ∑ i = 1 m p i l o g 2 p i Entropy(D) = -\sum_{i=1} ^ m p_i log_{2}p_i Entropy(D)=−i=1∑mpilog2pi
= − ∑ i = 1 m p i ( p i − 1 ) = -\sum_{i=1} ^ m p_i (p_i - 1) =−i=1∑mpi(pi−1)
= ∑ i = 1 m p i ( 1 − p i ) = \sum_{i=1} ^ m p_i (1 - p_i) =i=1∑mpi(1−pi)
= 1 − ∑ i = 1 m p i 2 = 1 - \sum_{i=1} ^ m p_i^{2} =1−i=1∑mpi2
结果:
G a i n ( D ) = 1 − ∑ i = 1 m p i 2 Gain(D) = 1 - \sum_{i=1} ^ m p_i^{2} Gain(D)=1−i=1∑mpi2
G a i n ( D , A ) = ∑ i = 1 m D m D G i n i ( D m ) Gain(D, A) = \sum_{i=1} ^ m \frac{D_m}{D} Gini(D_m) Gain(D,A)=i=1∑mDDmGini(Dm)
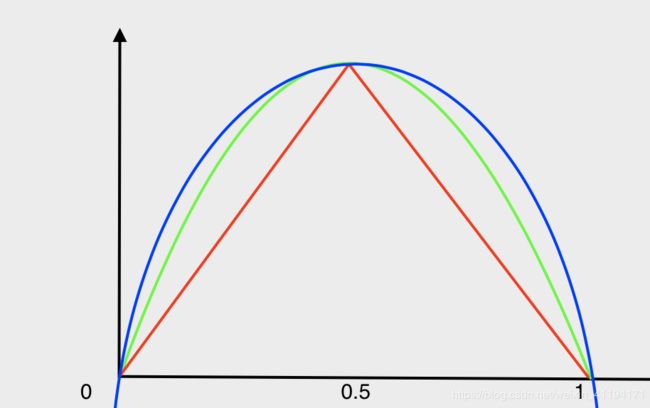
如上图所示,
-
红线与x轴组成的区域为标准分类误差率。
-
绿线与x轴组成的区域为基尼系数分类误差率。
-
蓝线与x轴组成的区域为信息熵分类误差率。
-
bootstrap:自助采样法,即有放回采样。
-
oob :oob全称out of bag。随机森林在bootstrap时大约有37%的样本没有取到,而这未取到的样本就是oob。
-
oob误差:用oob样本数据作为测试集时,计算得出的误差称为oob误差。
-
bagging:是一种集成学习的方法,基于bootstrap的采样方式。通过并行的方式将多个基学习器组合成一个强学习器。
[外链图片转存中…(img-lVXDR1MG-1593959645463)] -
随机森林:由多颗决策树组成,可以用于分类和预测。随机森林有两个随机,分别是:样本随机和特征随机。
随机森林分类和回归的策略
分类:采用投票的方式,少数服从多数。每个树会投给某个类别,取所有树投票数最多的类别作为随机森林的输出。
回归:一般采用平均法。取所有决策树的均值作为随机森林的输出。
随机森林公式
普通平均法:
G ( x ) = 1 m ∑ i = 1 m g i ( x ) G(x) = \frac{1}{m} \sum_{i=1} ^ m g_i(x) G(x)=m1i=1∑mgi(x)
上式中 g m ( x ) g_m(x) gm(x)为每个基学习器的值。
加权平均法:
G ( x ) = ∑ i = 1 m w i g i ( x ) G(x) = \sum_{i=1} ^ m w_i g_i(x) G(x)=i=1∑mwigi(x)
上式中 w i w_i wi为每个基学习器的权重。