期权、期货及其他衍生产品 第三章读书笔记 利用期货的对冲策略
期权、期货及其他衍生产品 第三章读书笔记 利用期货的对冲策略
- 基本原理
- 空头对冲
- 多头对冲
- 对冲对成本的锁定(基差为0)
- 拥护与反对对冲的观点
- 基差风险
- 基差
- 卖出资产所得实际价格
- 买入资产支付实际价格
- 基差风险
- 风险资产和对冲标的资产不一致
- 对合约的选择
- 交叉对冲
- 计算最优对冲比率(最小方差对冲比率)
- 最优合约数量
- 尾随对冲
- 股指期货
- 股指
- 我国的股指和股指期货
- 股票组合的对冲
- 当股票组合跟踪股指时
- 资本资产定价模型(Capital Asset Pricing Model,CAPM)
- 当股票组合不跟踪股指时
- 对冲股权组合的理由
- 改变组合的 β \beta β
- 锁定挑选股票的优势
- 向前滚动对冲
在期货市场上很多参与者都是对冲者,他们的目的是利用期货市场
来对冲自己面临的某种风险,这里的风险可能与原油价格、汇率、股票价格或其他变量的波动有关。完美对冲(perfect hedge)是指完全消除风险的策略,在实际中完美对冲极其罕见。因此,在大多数情况下,选取期货对冲就是指找出一种尽可能接近完美的对冲方式。
在这一章里,我们考虑建立对冲的一些基本问题:
什么时候应该采用期货空头?
什么时候应该采用期货多头?
应该选用哪一种期货合约?
采用期货对冲的最佳头寸又是什么?
注意:这里采用的都是保完即忘策略(hedge-and-forget strategy),也就是说,一旦设定对冲策略后,无须再对其进行调整。在第19章里则将考虑动态对冲策略(dynamic hedging strategy),这时对冲者要密切监视对冲策略,并经常调整头寸。
另外,在本章里我们首先将期货合约作为远期合约来处理(即忽略每天的结算),然后我们将讨论所谓的“跟踪因子”(tailing)调节量,这种调节量考虑了期货与远期合约的不同。
基本原理
当个人或公司选用期货产品来对冲风险时,目标是选择尽量使风险中性化的头寸。考虑这样一家公司,它已知在3个月后如果某商品的价格上涨1美分,公司将收入10000美元,但如果商品的价格下跌1美分,公司将损失10000美元。为了对冲风险,公司资金部主管应进入期货合约的空头来抵消风险:当商品价格上涨1美分时,期货将触发10000美元的损失;当商品价格下跌1美分时,期货将带来10000美元的收益。如果商品价格确实下跌,期货合约的收益会抵消公司其他业务的损失;如果商品价格上涨,期货的损失被公司其他业务的收益抵消。
如果资产价格上升公司会盈利,而当资产价格下跌公司会亏损的情况下,应当采用期货空头对冲。
如果资产价格下跌公司会有盈利,而资产价格上升公司会有亏损的情况下,应当采用期货多头对冲。
空头对冲
空头对冲(short hedge)指持有期货空头的对冲策略。
当对冲者已经拥有了某种资产并期望在将来某时刻卖出资产时,这时选择期货空头对冲是合理的。例如,一个养猪的农场主知道自己会在2个月后在当地市场出售活猪,他这时可以选择空头对冲。
在当前不拥有资产但在将来会拥有资产的情况下,也可以选择空头对冲。例如,一个美国出口商已知在3个月后将收进一笔欧元,出口商在欧元(同美元比较)升值时会有收益,而在欧元(同美元比较)贬值时会有损失,这时可以选择空头对冲。对冲策略在欧元升值时会产生损失,而在贬值时则会产生盈利,其作用是消除出口商的风险。
多头对冲
多头对冲(long hedge)指持有期货多头的对冲策略。
当公司已知在将来需要买入一定资产并想在今天将价格锁定时,可以采用多头对冲。
对冲对成本的锁定(基差为0)
以空头对冲为例介绍对冲对成本的锁定(基差为0),注意我们假定在交割月内对期货头寸平仓。如果允许交割发生,对冲的基本效果仍然是一样的。但是,履行交割的费用可能很昂贵并且非常不便。出于这一原因,即使对冲者将期货合约持有到交割月,实际交割通常也不会发生。像我们在今后讨论的那样,为了避免接受交割的可能性,持有期货多头的对冲者通常选择在交割期之前对期货进行平仓。
假定今天是5月15日,一位原油生产商刚刚签订了一份卖出100万桶原油的合约。合约所约定的价格为8月15日的市场价格。假设5月15日每桶原油的即期价格为80美元,8月份到期的原油期货价格为79美元。因为每份期货合约的规模为1000桶原油,因此原油生产商可以通过卖出1000份期货合约来对冲风险。如果原油生产商在8月15日平仓,这一交易策略的效果是将原油锁定在大约79美元的价格上。
假如在8月15日原油的即期价格为每桶75美元。公司因卖出原油而收入7500万美元。由于8月份是期货的交割月,所以在8月15日的期货价格应与这一天的即期价格(即75美元)非常接近,因此公司从每桶原油上赚取大约79-75=4(美元),即期货空头的总收益为400万美元。由卖出原油合约与期货合约一起所实现的是价格为大约每桶79美元,整体收入为7900万美元。
假定在8月15日原油的即期价格为每桶85美元。公司以每桶85美元卖出石油,而因持有原油期货每桶亏损的数量大约为85-79=6(美元)。这时,卖出原油和期货的总收入大约为7900万美元。不难看出,在不同情形下,公司的整体收入总是大约为7900万美元。
注意,这个例子中的背景为“在8月15日的期货价格应与这一天的即期价格(即75美元)非常接近”,即基差为0,因此把价格锁定在了5月15日时“8月份到期的原油期货价格为79美元”上。
拥护与反对对冲的观点
持对冲的观点非常明显,因此我们不再重述。大多数非金融公司的业务为制造业、零售业、批发业或服务业,这些公司没有预见利率、汇率以及商品价格变化的特殊能力。因此,对于这些公司而言,对冲由这些市场变量所引起的风险很有意义,因为这样公司可以集中精力发展自己的主要业务,而这些主要业务正是这些公司的特长。通过对冲,公司可以避免由于商品价格急剧上涨而使购买费用增大所带来的不快。
对冲是减少风险的一种方法,因此应当受到多数高管的欢迎。在实际中,许多理论和实际方面的原因会使公司不进行对冲。从理论上讲,当公司股东持有一个风险分散良好的组合时,公司所面临的许多风险会被消除掉,因此并不需要公司去对冲这些风险。从实际上讲,如果同行业里的竞争对手都不进行对冲,这时选择对冲会增大而不是减小风险。还有,当公司从价格变动中得到盈利,但在对冲中遭受损失时,公司资金部主管可能会担心其他高管会对这一情形进行批评。
基差风险
到目前为止,我们所考虑的对冲例子都完美得令人难以置信。在这些例子中,对冲者可以确定将来买入资产的准确日期,从而可以利用期货合约来消除在那一天几乎所有由于资产价格变动而带来的风险。在实际中对冲时常常并没这么容易,部分原因如下:
(1)需要对冲价格风险的资产与期货合约的标的资产可能并不完全一样;(交叉对冲)
(2)对冲者可能无法确定买入或卖出资产的准确时间;
(3)对冲者可能需要在期货到期月之前将期货平仓。
这些问题就引起了所谓的基差风险(basis risk)。
基差
在对冲意义下,基差(basis)的定义如下:【这是通常的定义】
基差=被对冲资产的即期价格-用于对冲的期货合约价格
随着时间的变化,即期价格变化与特定月份期货的价格变化并不一定相同,因而会导致基差的变化。当基差变大时称为是基差增强(strengthening of the basis);当基差变小时称为基差减弱(weakening of the basis)。
为了讨论基差风险的性质,对以下符号进行定义:
S 1 : 在 时 刻 t 1 的 即 期 价 格 S 2 : 在 时 刻 t 2 的 即 期 价 格 F 1 : 在 时 刻 t 1 的 期 货 价 格 F 2 : 在 时 刻 t 2 的 期 货 价 格 b 1 : 在 时 刻 t 1 的 基 差 b 2 : 在 时 刻 t 2 的 基 差 S_1:在时刻t_1的即期价格\\ S_2:在时刻t_2的即期价格\\ F_1:在时刻t_1的期货价格\\ F_2:在时刻t_2的期货价格\\ b_1:在时刻t_1的基差\\ b_2:在时刻t_2的基差 S1:在时刻t1的即期价格S2:在时刻t2的即期价格F1:在时刻t1的期货价格F2:在时刻t2的期货价格b1:在时刻t1的基差b2:在时刻t2的基差
假定在时刻 t 1 t_1 t1建立对冲头寸,并在时刻 t 2 t_2 t2平仓。作为例子,我
们考虑如下情形:在刚建立对冲时,即期和期货价格分别是2.50美元和2.20美元,在对冲平仓时,即期和期货价格分别是2.00美元和1.90美元。这意味着 S 1 = 2.50 , F 1 = 2.20 , S 2 = 2.00 和 F 2 = 1.90 S_1=2.50,F_1=2.20,S_2 =2.00和F_2 =1.90 S1=2.50,F1=2.20,S2=2.00和F2=1.90。
因此,由基差定义 b 1 = S 1 − F 1 b_1 =S_1 -F_1 b1=S1−F1和 b 2 = S 2 − F 2 b_2 =S_2 -F_2 b2=S2−F2得出 b 1 = 0.30 b_1=0.30 b1=0.30和 b 2 = 0.10 b_2 =0.10 b2=0.10。
卖出资产所得实际价格
对冲者已知将在时刻 t 2 t_2 t2卖出资产,并在 t 1 t_1 t1时持有了期货空头。资产所实现的价格为 S 2 S_2 S2,期货的盈利为 F 1 − F 2 F_1-F_2 F1−F2 (这里是做空,若 F 1 − F 2 F_1-F_2 F1−F2为正,则盈利,否则即亏损,但无论那种情况,不影响分析)。
因此对冲后,卖出资产所得实际价格为 S 2 + F 1 - F 2 = F 1 + b 2 S_2 +F_1 -F_2 =F_1 +b_2 S2+F1-F2=F1+b2
根据以上的例子,这里卖出资产所得实际价格为为2.30美元。
借助于对卖出资产所得实际价格的分析,在时刻 t 1 t_1 t1 ,已知 F 1 F_1 F1的价格,如果在这个时刻也知道 b 2 b_2 b2 ,那么这时可以构造完美对冲。对冲风险与 b 2 b_2 b2的不确定性有关,此风险即为基差风险。
买入资产支付实际价格
公司已知在时刻 t 2 t_2 t2将购买资产,因而在时刻 t 1 t_1 t1进行了多头对冲。买入资产所付价格为 S 2 S_2 S2,对冲的损失为 F 1 − F 2 F_1 -F_2 F1−F2(这里是做多,收益为 F 2 − F 1 F_2 -F_1 F2−F1,但这里考虑的是购买资产的成本,因此为 F 1 − F 2 F_1 -F_2 F1−F2)。
实施对冲以后,买入资产支付的实际价格为 S 2 + F 1 - F 2 = F 1 + b 2 S_2 +F_1 -F_2 =F_1 +b_2 S2+F1-F2=F1+b2
这与前面的表达式一样,在本例中上式等于2.30美元。在时刻 t 1 t_1 t1已知 F 1 F_1 F1的价格, b 2 b_2 b2代表基差风险。
基差风险
基差风险可以使得对冲者的头寸得到改善或得到恶化。假设一家公司计划在将来卖出资产,决定采用空头对冲,如果基差在意想不到的情况下增强(即增大),对冲者的头寸会有所改善,这是因为在考虑了期货的盈亏之后,卖出资产时会拿到更好的价格;如果基差在意想不到的情况下减弱(减小),对冲者的头寸有所恶化。
风险资产和对冲标的资产不一致
有时给对冲者带来风险的资产与用于对冲的合约标的资产是不一样的,这种情形下的对冲叫交叉对冲(cross hedging)。在这种情况下,基差风险一般会更大。
定义 S 2 ∗ S_2^* S2∗为期货合约标的资产在时刻 t 2 t_2 t2的价格。与上面相同, S 2 S_2 S2是被对冲资产在时刻 t 2 t_2 t2的价格。通过对冲,公司确保购买或出售资产的价格为
F 1 + ( S 2 ∗ − F 2 ) + ( S 2 − S 2 ∗ ) F_1+(S_2^*-F_2)+(S_2-S_2^*) F1+(S2∗−F2)+(S2−S2∗)
其中, S 2 ∗ − F 2 S_2^*-F_2 S2∗−F2和 S 2 − S 2 ∗ S_2-S_2^* S2−S2∗代表基差的两个组成部分,前者代表当被对冲资产与期货合约标的资产一致时,对冲所产生的基差,而后者是由于被对冲资产与期货合约标的资产不一样而产生的基差。
对合约的选择
影响基差风险的一个关键因素是选择用来对冲的期货合约。这里的
选择包括两部分:
(1)对期货合约标的资产的选择;
(2)对交割月份的选择。
如果被对冲的资产刚好与期货合约的标的资产吻合,这里的第一个选择一般会很容易。在其他情形下,对冲者必须通过仔细分析来确定哪一种期权价格与被对冲资产的价格有最紧密的相关性。
交割月份的选择跟多个因素有关。在本章前面的例子中,当假定对冲的期限对应于某种期货的交割月份时,我们选择了对应于这个交割月份的期货合约。事实上,在这种情形下对冲者往往会选择一个在稍后月份交割的期货合约。因为在这种情况下,处于交割月份中的期货价格有时会很不稳定。同时,在交割月份多头对冲者会承受必须接受实物交割的风险,因为资产交割的花费很大,而且极不方便。
一般来讲,当对冲的期限与期货交割月份之间的差距增大时,基差
风险也会随之增大。一种经验法则(rule of thumb)是尽量选择与对冲期限最近却在其之后的交割月份。假定某一资产上期货的到期月分别为3月、6月、9月和12月。对于在12月、1月、2月到期的对冲,应当选择3月份的合约;对于在3月、4月、5月到期的对冲,应当选择6月份的合约等。在实际中,短期限期货合约往往具有最强的流动性。
交叉对冲
在之前的例子中,对冲时所用期货的标的资产与被对冲的资产是一样的。当两种资产不同时就会出现交叉对冲(cross hedging)。例如,某家航空公司对航空燃料油的未来价格有些担心,但是由于没有航空燃料油的期货,这家公司也许会利用民用燃料油期货合约来对冲风险。
对冲比率(hedging ratio)是指持有期货合约的头寸数量与资产风险敞口数量的比率。当期货标的资产与被对冲资产一样时,对冲比率当然应该取为1.0。这正是我们在以上所有例子中所采用的对冲比率。例如,对冲者的风险敞口为20000桶原油,期货所对应的资产交割数量刚好与这个头寸相等。
当采用交叉对冲时,将对冲比率取为1.0并不一定是最优的选择。对冲者采用的对冲比率应当使被对冲后头寸价格变化的方差达到极小。
计算最优对冲比率(最小方差对冲比率)
最小方差对冲比率取决于即期价格的变化与期货价格变化之间的关系。
Δ S : 在 对 冲 期 限 内 , 即 期 价 格 S 的 变 化 Δ F : 在 对 冲 期 限 内 , 期 货 价 格 F 的 变 化 \Delta S:在对冲期限内,即期价格S的变化\\ \Delta F:在对冲期限内,期货价格F的变化 ΔS:在对冲期限内,即期价格S的变化ΔF:在对冲期限内,期货价格F的变化
用 h ∗ h^* h∗表示最小方差对冲比率,可以证明 h ∗ h^* h∗是ΔS对ΔF进行线性回归时所产生的最优拟合直线(best-fit line)的斜率(见下图所示)。
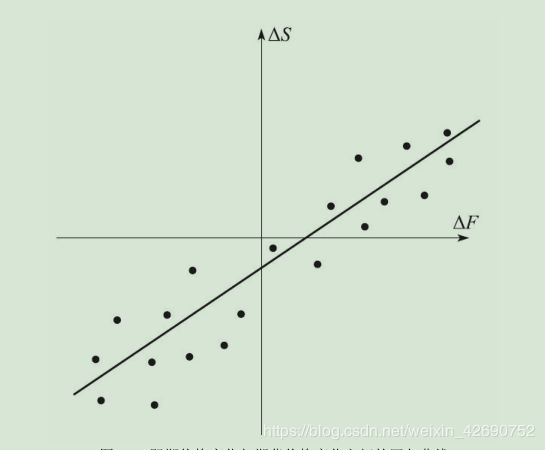
这个结果在直观上很合理:我们希望 h ∗ h^* h∗是当F变化一定数量时,S平均变化的比例。
h ∗ = ρ σ S σ F h^*=\rho \frac{\sigma_S}{\sigma_F} h∗=ρσFσS
其中 σ S σ_S σS是ΔS的标准差, σ F σ_F σF是ΔF的标准差,ρ是两者之间的相关系数。
最佳对冲比率等于ΔS与ΔF之间的相关系数乘以ΔS的标准差与ΔF的标准差之间的比率。
如果ρ=1和 σ F = σ S σ_F =σ_S σF=σS ,对冲比率 h ∗ h^* h∗为1.0:因为这时期货价格变化正好等于即期价格的变化,这一结果正是我们所预期的。如果ρ=1和 σ F = 2 σ S σ_F =2σ_S σF=2σS ,最佳对冲比率 h ∗ h^* h∗为0.5:因为这时期货价格的变化幅度是即期价格变化幅度的两倍,这一结果也正好是我们所预期的。
对冲效率(hedge effectiveness)可以被定义为对冲所消除的方差量占总方差的比例,这正是将ΔS对ΔF进行线性回归的 R 2 R^2 R2系数,等于 ρ 2 ρ^2 ρ2。
式中的参数ρ、 σ F σ_F σF和 σ S σ_S σS通常是通过ΔS和ΔF的历史数据来估计(这里所隐含的假设是从某种意义上,历史反映未来)。
最优合约数量
为了计算对冲所用的合约数量,定义:
Q A : 被 对 冲 头 寸 的 数 量 ( 单 位 数 量 ) ; Q F : 1 份 期 货 合 约 的 规 模 ( 单 位 数 量 ) ; N ∗ : 用 于 对 冲 的 最 优 期 货 合 约 数 量 。 Q_A:被对冲头寸的数量(单位数量);\\ Q_F:1份期货合约的规模(单位数量);\\ N^*:用于对冲的最优期货合约数量。 QA:被对冲头寸的数量(单位数量);QF:1份期货合约的规模(单位数量);N∗:用于对冲的最优期货合约数量。
在完美对冲情形下,应当有下面的恒等式
N ∗ Q F Δ F = Q A Δ S N^* Q_F \Delta_F = Q_A \Delta_S N∗QFΔF=QAΔS
该等式意味着用于对冲的期货合约的盈利(亏损)正好与被对冲资产的亏损(盈利)完全相同
最优对冲比例可以近似为 h ∗ = Δ S Δ F h^*=\frac{\Delta_S}{\Delta_F} h∗=ΔFΔS,从而可以得到用于对冲的最优期货合约份数
N ∗ = h ∗ Q A Q F N^*=h^* \frac{Q_A}{Q_F} N∗=h∗QFQA
某航空公司预计在1个月后需要购买200万加仑航空燃料油,并决定利用民用燃料油期货来对冲。根据连续15个月每加仑航空燃料油价格变化ΔS,以及用于对冲的民用燃料油期货价格的相应变化ΔF。利用通常计算标准差和相关系数的公式,可以得出 σ F = 0.0313 , σ S = 0.0263 , ρ = 0.928 σ_F =0.0313,σ_S=0.0263,\rho=0.928 σF=0.0313,σS=0.0263,ρ=0.928。
可以得出最小方差对冲比率 h ∗ h^* h∗ 为
h ∗ = 0.928 ∗ 0.0263 0.0313 = 0.78 h^*=0.928 * \frac{0.0263}{0.0313}=0.78 h∗=0.928∗0.03130.0263=0.78
每份CME集团的民用燃料油期货是关于42000加仑民用燃料油,因此最优合约的数量为
0.78 ∗ 2000000 42000 = 37.03 0.78 * \frac{2000000}{42000} = 37.03 0.78∗420002000000=37.03
近似到最近的整数,合约数量为37
尾随对冲
如果我们用来对冲的是远期合约,上面的分析是正确的,这是因为我们感兴趣的确实是在对冲期限内远期价格变化和即期价格变化的相关程度。当利用期货进行对冲时,会存在期货合约的每天结算和一系列持续1天的对冲交易问题。为了反映这个特征,分析员有时计算期货价格每天百分比变化和即期价格每天百分比变化之间的相关系数,将此系数记为 ρ ^ \hat{\rho} ρ^ 。另外,将期货价格每天百分比变化的标准差记为 σ ^ F \hat{\sigma}_F σ^F,即期价格每天百分比变化的标准差记为 σ ^ S \hat{\sigma}_S σ^S 。
如果S和F为即期和期货价格,1天价格变化的标准差分别为 S σ ^ S S\hat{\sigma}_S Sσ^S和 F σ ^ F F\hat{\sigma}_F Fσ^F。因此。期限为1天的对冲
比率为
ρ S σ ^ S F σ ^ F \rho \frac{S\hat{\sigma}_S}{F\hat{\sigma}_F} ρFσ^FSσ^S
在此基础上,可以计算得到为了下一天对冲需要持有的合约数量为
N ∗ = ρ S σ ^ S Q A F σ ^ F Q F N^*=\rho \frac{S\hat{\sigma}_SQ_A}{F\hat{\sigma}_FQ_F} N∗=ρFσ^FQFSσ^SQA
采用以上结果来计算对冲合约数量的做法有时被称为尾随对冲(tailing the hedge),这一结果也可以表述为
N ∗ = h ^ V A V F N^*=\hat{h} \frac{V_A}{V_F} N∗=h^VFVA
其中, V A V_A VA为被对冲头寸的实际货币价值(= S Q A SQ_A SQA), V F V_F VF 为一个期货合约的货币价值(= F Q F FQ_F FQF ),而 h ^ \hat{h} h^的定义则与 h ∗ h^* h∗类似
h ^ = ρ ^ σ ^ S σ ^ F \hat{h}=\hat{\rho} \frac{\hat{\sigma}_S}{\hat{\sigma}_F} h^=ρ^σ^Fσ^S
从理论上讲,这个结果说明应当将对冲期货的头寸随着 V A V_A VA和 V F V_F VF的变化而调整,但在实际中,在一天内对冲的变化很小,通常被忽略。
股指期货
下面开始研究股指期货,以及如何将其用于对冲或管理与股票价格有关的风险敞口。
股指(stock index)跟踪一个虚拟股票组合的价值变化,每个股票在组合中的权重等于股票组合投资于这一股票的比例。在计算中,通常不包括股息,因此股指是用于跟踪在这一组合上投资的资本增值/亏损(capital gain/loss)。
需要注意的是,组合中每个股票的权重不一定不变。有些指数的建立是在一些股票中每样取一只,这时股票的权重与其市场价格成比例,当股票分股时做适当调整。另一些股指的构造使得权重与股票的市场资本总价值(股票价格×发行的数量)成比例,这时股票组合会对股票的分股、股票形式的股息和新股发行自动进行调整。
股指
道琼斯工业平均指数 Dow Jones Industrial Average是基于30美国蓝筹(blue-chip)股票所组成的股票组合,权重与股票价格成比例。CME集团有两种关于这个指数的合约:一种期货的标的变量是10美元乘以指数值;另一种(Mini DJ Industrial Average)是5美元乘以指数值,Mini合约在市场上交易最活跃。
标准普尔500指数 S&P 500是基于一个包括500种股票的组合,这500种股票的组成为:400种工业股,40种公共事业股,20种交通业股以及40种金融股。在任何时刻,股票的权重与该股票的总市值成比例。这些股票都是在NYSE Euronext或Nasdaq OMX上市。CME集团有两种关于标普500的期货合约:一种是关于250美元乘以指数;另一种(Mini S&P 500contract)是关于50美元乘以指数,Mini合约在市场上交易最活跃。
纳斯达克100指数 Nasdaq 100 是基于由全国债券交易自动报价服务联合会(National Association of Securities Dealers Automatic Quotations Service)交易的100种股票所组成的组合。CME集团交易所交易两种与这个指数有关的合约:一种是关于100美元乘以指数;另一种(Mini Nasdaq 100Contract)是关于20美元乘以指数,Mini合约在市场上交易最活跃。
我国的股指和股指期货
上证综合指数 简称 上证综指是由上海证券交易所编制的股票指数,于1991年7月15日起编制并正式对外发布。该股票指数的样本为所有在上海证券交易所挂牌上市的股票(包括A股和B股)。上证综指的基准日定为1990年12月19日,基准日的指数定为100点,该指数的权重是以股票的市值(股票价格×发行数量)为依据。
上证成份指数 简称 上证180指数是上海证券交易所对原上证30指数进行了调整并更名而成的,其样本股是在所有上海证券交易所交易的A股股票中抽取最具市场代表性的180种样本股票,自2002年7月1日起正式发布,指数每半年调整一次成分股,每次调增比例一般不超过10%,特殊情况时也可能对样本进行临时调整。
上证50指数是上海证券交易所于2004年1月2日起对外发布的指数,该指数是根据流通市值、成交金额对上证180指数样本股进行综合排名,从中挑选出规模大、流动性最好的50只股票组成样本股,以综合反映上海证券市场最具影响力的一批龙头企业的整体状况。与上证180指数相同的是,上证50指数每半年调整一次成分股,每次调整比例一般不超过10%,特殊情况时也可能对样本进行临时调整。
深证成分股指数 简称 深证成指 是深圳证券交易所编制的一种成分股指数,是从上市的所有股票中抽取具有市场代表性的40家上市公司的股票作为计算对象,并以流通股市值为依据计算得出的加权股价指数,综合反映深交所上市A、B的股价走势。深证成指的基准日定为1994年7月20日,基准日指数定为1000点。
沪深300指数 简称 沪深300是由上海证券交易所、深圳证券交易所于2005年4月8日联合发布的反映A股市场整体趋势的指数,是选取了在这两家交易所挂牌交易的300只流动性强和规模大的代表性A股股票作为样本编制而成的指数,并以流通股市值为依据计算得出,指数基准日为2004年12月31日,基准点为100点。样本股调整时间分别是每年6月和12月的第二个星期五收盘后的下一个交易日,每次调整数量一般不超过10%。
中证500指数是由中证指数有效公司编制,挑选了沪深证券交易所中具有代表性的中小市值公司组成样本股,以便综合反映沪深证券市场内中小市值公司的整体状况。
中国金融期货交易所 简称 中金所 是经国务院同意、中国证监会批准设立的,专门从事金融期货、期权等金融衍生产品交易与结算的公司制交易所。目前,我国的股指期货合约就是由中金所推出并在中金所挂牌交易的。
中金所是由上海期货交易所、郑州商品交易所、大连商品交易所、上海证券交易所、深圳证券交易所共同发起,于2006年9月8日在上海正式挂牌成立。
中金所实施会员分级结算制度,会员分为结算会员和交易会员。结算会员按照业务范围分为交易结算会员、全面结算会员和特别结算会员,实行会员分级结算制度,形成多层次风险控制体系,保障市场安全运行。
| 合约标的股指 | 沪深300指数 | 上证50指数 | 中证500指数 |
|---|---|---|---|
| 合约乘数 | 每点300元 | 每点300元 | 每点200元 |
| 报价单位 | 指数点 | 同 | 同 |
| 最小变动价位 | 0.2点 | 同 | 同 |
| 合约月份 | 当月、下月及随后两个季月 | 同 | 同 |
| 交易时间 | 上午9:15-11:30 下午13:00-15:15 | 同 | 同 |
| 最后交易日交易时间 | 上午9:15-11:30 下午13:00-15:00 | 同 | 同 |
| 每日价值最大波动限制 | 上一个交易日结算价的正负10% | 同 | 同 |
| 最低交易保证金 | 合约价值的8% | 同 | 同 |
| 最后交易日 | 合约到期月份的第三个周五,遇国家法定假日顺延 | 同 | 同 |
| 交割日期 | 同最后交易日 | 同 | 同 |
| 交割方式 | 现金交割 | 同 | 同 |
| 交易代码 | IF | IH | IC |
| 首次上市时间 | 2010年4月16日 | 2015年4月16日 | 2015年4月16日 |
股票组合的对冲
当股票组合跟踪股指时
股指期货可用于对冲风险分散良好的股票投资组合。
V A : 股 票 组 合 的 当 前 价 值 V F : 一 份 期 货 的 当 前 价 值 ( 期 货 价 格 ∗ 期 货 规 模 ) V_A:股票组合的当前价值\\ V_F:一份期货的当前价值(期货价格*期货规模) VA:股票组合的当前价值VF:一份期货的当前价值(期货价格∗期货规模)
如果组合是为了跟踪股票指数,最优对冲率 h ∗ h^* h∗为1.0,那么可以得到需要持有的期货空头合约数量为
N ∗ = V A V F N^*=\frac{V_A}{V_F} N∗=VFVA
例如,某股票组合跟踪的是标普500,价值为5050000美元。股指的当前值为1010,每一份期货是关于250美元乘以股指。这时, V A = 5050000 V_A =5050000 VA=5050000和 V F = 1010 × 250 = 252500 V_F =1010×250=252500 VF=1010×250=252500。因此,对冲者应该持有20份期货空头合约来对冲这个股票组合。
资本资产定价模型(Capital Asset Pricing Model,CAPM)
CAPM模型是投资组合管理人员一件有用的工具,该模型常常被用来作为检验投资组合表现的标准。
CAPM模型的推导建立许多假设之上,其中包括:
(1)投资者只关心资产投资组合回报的期望值与标准差;
(2)两个资产之间的相关性只是因为这些资产与市场组合相关,这个假设等价于资产回报只取决于一个因子;
(3)投资人只关心在某一特定时间区间上的投资回报,而且所有投资人所选定的时间区间均相同;
(4)投资人可以按相同的无风险利率借入或借出资金;
(5)税务不影响投资决策;
(6)所有投资人对资产回报的期望值、标准差以及对资产之间的相关系数都有相同的估计。
CAPM模型将资产的回报期望值与回报风险联系起来,资产的回报风险分成两个部分:**系统风险(systematic risk)**与将市场作为一个整体的回报有关,这一部分风险无法被分散掉;非系统风险(nonsystematic risk)是资产独有的并可以通过选取一个由不同资产组成的交易组合来分散掉。CAPM的讨论集中于系统风险
预 期 资 产 回 报 = R F + β ( R M − R F ) 预期资产回报=R_F+\beta (R_M-R_F) 预期资产回报=RF+β(RM−RF)
其中, R M R_M RM是由所有可投资资产构成的组合产生的回报, R F R_F RF是无风险投资回报,参数 β \beta β是对系统风险的一种度量。
由所有可投资资产构成的组合产生的回报 R M R_M RM,叫市场回报(return on the market),通常以像标普500这样充分分散化的股票指数来作为近似。
β \beta β是衡量资产回报对于市场回报的敏感程度,通常由历史数据来估计。将资产高于无风险利率的额外回报与市场交易组合高于无风险利率的额外回报进行线性回归时, β \beta β是回归方程的斜率。
当 β \beta β=0时,敏感度为零(即无敏感度),这时资产无系统性风险,资产的回报期望值等于无风险利率;
当 β \beta β=0.5时,资产回报率超过无风险利率的那一部分(平均来讲)是市场回报率超出无风险利率的一半;
当 β \beta β=1时,资产回报的期望值等于市场回报,
假定无风险利率 R F R_F RF为5%,市场回报率为13%。
当 β \beta β为0时,回报期望为5%;
当 β \beta β等于0.75时,回报期望为0.05+0.75×(0.13-0.05)=0.11,即11%。
当资产是单个股票时,所得出的回报期望并非真实回报的一个有效预测,但当资产是一个充分分散化后的股票组合时,预测效果就要好很多。以下关系式可以作为对冲分散化组合的基础
分 散 化 的 组 合 回 报 = R F + β ( R M − R F ) 分散化的组合回报=R_F +\beta(R_M -R_F) 分散化的组合回报=RF+β(RM−RF)
其中 β \beta β是组合的beta,该系数可以根据组合中每个股票 β \beta β的加权平均来计算。
当股票组合不跟踪股指时
当股票组合不跟踪股指时,我们可以采用资本资产定价模型(CAPM)中的 β \beta β值来确定持有期货空头的数量。 β \beta β是将组合超过无风险利率的收益与股票市场超过无风险利率的收益进行回归所产生的最佳拟合直线的斜率。
当 β \beta β=1时,组合收益往往跟踪市场收益;
当 β \beta β=2时,组合超过无风险利率的收益等于股票市场超过无风险收益的两倍;
当 β \beta β=0.5时,组合超过无风险利率的收益等于股票市场超过无风险收益的一半。
一个 β \beta β值等于2.0的组合对市场的敏感度是一个 β \beta β值等于1.0的组合的两倍。因此,为了对冲这一组合,我们将需要两倍数量的合约。
类似地,一个 β \beta β值等于0.5的组合对市场的敏感度是一个 β \beta β值等于1.0的组合的一半,因此我们只需要一半数量的合约来对冲风险。
N ∗ = β V A V F N^*=\beta \frac{V_A}{V_F} N∗=βVFVA
将该式和交叉对冲中的公式进行对比,可以发现实际上 h ∗ = β h^*=\beta h∗=β。这一结果是合理的,对冲比率 h ∗ h^* h∗是将组合价值在一天内的百分比变化对于股指期货价格在一天内的百分比变化做线性回归时的最优拟合直线的斜率, β \beta β是组合变化对股指变化做线性回归时的最优拟合直线的斜率。
假定利用4个月期限的期货合约来对组合在今后3个月内的价值进行对冲。假设
标普500股指当前值=1000
标普500股指期货价格=1010
组合价值=5050000美元
无风险利率=每年4%
股指票息收益率=每年1%
组合的β=1.5
1份期货合约是交割250美元乘以股指,因此,
V F = 250 × 1010 = 252500 V_F =250×1010=252500 VF=250×1010=252500
计算可得对冲组合所需要持有的空头期货合约数量为
1.5 ∗ 5050000 252500 = 30 1.5*\frac{5050000}{252500}=30 1.5∗2525005050000=30
假定股指在3个月后为900,期货价格为902,期货空头的收益为
30 ∗ ( 1010 − 900 ) ∗ 250 = 810000 美 元 30*(1010-900)*250=810000 美元 30∗(1010−900)∗250=810000美元
股指的亏损为10%。股指每年支付1%的股息收益率,或每3个月0.25%。因此,将股息考虑在内时,股指投资者在3个月里的收益为-9.75%。由于组合的β是1.5,由于资本资产定价模型:
组 合 的 收 益 期 望 = 无 风 险 利 率 + 1.5 × ( 股 指 收 益 − 无 风 险 利 率 ) 组合的收益期望=无风险利率+1.5×(股指收益-无风险利率) 组合的收益期望=无风险利率+1.5×(股指收益−无风险利率)
3个月期的无风险利率大约为1%,因此,组合在3个月内的收益期望(%)为
1.0 + [ 1.5 × ( − 9.75 − 1.0 ) ] = − 15.125 1.0+[1.5×(-9.75-1.0)]=-15.125 1.0+[1.5×(−9.75−1.0)]=−15.125
因此组合在3个月后价值的期望(包括股息)为
5050000 × ( 1 − 0.15125 ) = 4286187 ( 美 元 ) 5050000×(1-0.15125)=4286187(美元) 5050000×(1−0.15125)=4286187(美元)
在考虑对冲收益后,对冲者头寸价值的期望值为
4286187 + 810000 = 5096187 ( 美 元 ) 4286187+810000=5096187(美元) 4286187+810000=5096187(美元)
类似地,计算可以发现,3个月时的股指价格从900变化到1100,整体头寸在3个月时的价值几乎没有变化。
对冲股权组合的理由
对上面的例子进行分析,组合价值为5050000美元,实施对冲策略后在3个月后的头寸价值为5096187美元,高了大约1%。这一结果并不奇怪,因为无风险利率为每年4%,或每3个月1%。实施对冲后使得对冲者的头寸按无风险利率增长。
那么,下面就会产生一个问题:为什么要采用期货合约来对冲呢?为了取得无风险利率的收益,对冲者只需要变卖资产,并将得到的资金投放于类似短期国债之类的无风险产品即可。
对于上面问题的答案是:如果对冲者感觉组合中的股票选取的很好,那么实施对冲是有道理的。在这种情况下,对冲者对市场的整体风险很不确定,却确信组合中的股票收益会高于市场的收益(对组合 β \beta β值进行调整之后)。一个对冲者可以采用股指期货来消除因市场变动而触发的风险,从而使对冲者仅仅暴露于股票组合与市场的相对表现中。
改变组合的 β \beta β
在上文的例子中,对冲者的β值被降低到0,因此对冲者的收益期望几乎与指数的表现无关。有时也可以利用期货合约来调整组合的 β \beta β,而不是将 β \beta β值降低到0。
为了将组合的 β \beta β从1.5转变为0.75,我们需要持有空头的合约数量应当为15,而不是30;当要将组合的 β \beta β由1.5转变为2.0,需要持有10个期权的多头,等等。通常来讲,当将组合的Beta从 β \beta β变为 β ∗ \beta^* β∗时,如果 β \beta β> β ∗ \beta^* β∗,所持期货空头的数量应当为
( β − β ∗ ) V A V F (\beta-\beta^*)\frac{V_A}{V_F} (β−β∗)VFVA
如果 β < β ∗ \beta<\beta^* β<β∗,所持期货多头的数量应当为
( β ∗ − β ) V A V F (\beta^*-\beta)\frac{V_A}{V_F} (β∗−β)VFVA
锁定挑选股票的优势
假设你擅长于挑选比市场表现更好的股票。你拥有一只股票或一个小的股票组合。你不知道在今后几个月内股票市场的表现将会如何,但你非常确认你持有的股票将比市场表现要好,你这时该如何做呢?
你应该持有数量等于 β V A / V F \beta V_A /V_F βVA/VF的股指期货合约空头,其中 β \beta β为你所持有股票的Beta值, V A V_A VA为持有的股票价值, V F V_F VF为1份股指期货合约的价值。如果你的股票投资组合比一个具有同样 β \beta β但风险分散很好的组合表现要好,你这时就会赚钱。
向前滚动对冲
有时对冲的期限要比所有能够利用的期货期限更长,这时对冲者必须对到期的期货进行平仓,同时再进入具有较晚期限的合约。这样可以将对冲向前滚动很多次。这种做法被称为向前滚动对冲(stack and roll)。
考虑某家公司,它希望利用期货空头来减少在将来时刻T收到某
个资产时所带来的风险。如果在市场上存在期货合约1,2,3,…n(并不一定目前都存在),其到期日一个比一个更晚。公司可以采用以下策略:
在 t 1 t_1 t1时刻:进入合约1的空头
在 t 2 t_2 t2时刻:对合约1平仓;进入合约2的空头
在 t 3 t_3 t3时刻:对合约2平仓;进入合约3的空头
…
在 t n t_n tn时刻:对合约n-1平仓;进入合约n的空头
在T时刻,对合约n平仓