Codeforces Round #627 (Div. 3)F - Maximum White Subtree【DFS】

F. Maximum White Subtree

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a tree consisting of nn vertices. A tree is a connected undirected graph with n−1n−1 edges. Each vertex vv of this tree has a color assigned to it (av=1av=1 if the vertex vv is white and 00 if the vertex vv is black).

You have to solve the following problem for each vertex vv: what is the maximum difference between the number of white and the number of black vertices you can obtain if you choose some subtree of the given tree that contains the vertex vv? The subtree of the tree is the connected subgraph of the given tree. More formally, if you choose the subtree that contains cntwcntw white vertices and cntbcntb black vertices, you have to maximize cntw−cntbcntw−cntb.

Input

The first line of the input contains one integer nn (2≤n≤2⋅1052≤n≤2⋅105) — the number of vertices in the tree.

The second line of the input contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤10≤ai≤1), where aiai is the color of the ii-th vertex.

Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi, the labels of vertices it connects (1≤ui,vi≤n,ui≠vi(1≤ui,vi≤n,ui≠vi).

It is guaranteed that the given edges form a tree.

Output

Print nn integers res1,res2,…,resnres1,res2,…,resn, where resiresi is the maximum possible difference between the number of white and black vertices in some subtree that contains the vertex ii.

Examples

input

Copy

9
0 1 1 1 0 0 0 0 1
1 2
1 3
3 4
3 5
2 6
4 7
6 8
5 9

output

Copy

2 2 2 2 2 1 1 0 2 

input

Copy

4
0 0 1 0
1 2
1 3
1 4

output

Copy

0 -1 1 -1 

Note

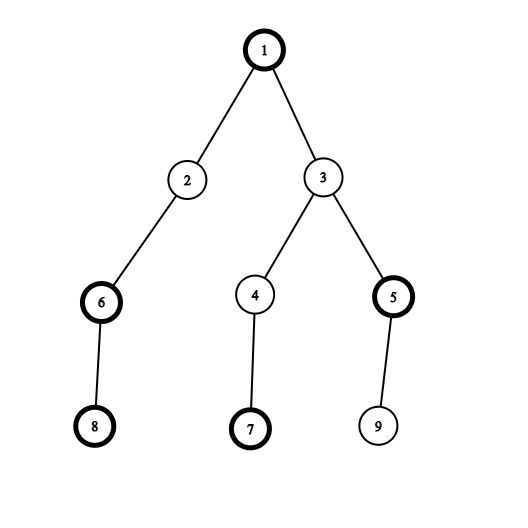
The first example is shown below:

转存失败重新上传取消

The black vertices have bold borders.

In the second example, the best subtree for vertices 2,32,3 and 44 are vertices 2,32,3 and 44 correspondingly. And the best subtree for the vertex 11 is the subtree consisting of vertices 11 and 33.

题意：给一棵树，每个节点是0或1，对于每个节点，求出包含这个节点的所有子树中，1的数量-0的数量 的最大值。

分析：固定root，第一遍dfs只处理子节点，若dp[son]>0，则dp[i]+=dp[son]，第二遍dfs再处理一下父亲节点。

#include 

using namespace std;
vector v[200004];
int a[200004];
int dp[200004];

int dfs1(int u, int pre) {
    int ans = 0;
    if (a[u] == 1)ans++;
    else ans--;
    for (int i = 0; i < v[u].size(); ++i) {
        int nxt = v[u][i];
        if (nxt == pre)continue;
        int res = dfs1(nxt, u);
        if(res>0)ans += res;
    }
    return dp[u]=ans;
}

void dfs2(int u,int pre){
    if(pre!=-1){
        int p = dp[pre] - (dp[u]<0?0:dp[u]);
        dp[u] = dp[u]+(p>0?p:0);
    }
    for (int i = 0; i < v[u].size(); ++i) {
        if(v[u][i] == pre)continue;
        dfs2(v[u][i],u);
    }
}
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < n - 1; ++i) {
        int x, y;
        scanf("%d%d", &x, &y);
        v[x].push_back(y);
        v[y].push_back(x);
    }
    dfs1(1,-1);
    dfs2(1,-1);
    for (int i = 1; i <= n; ++i) {
        printf("%d ",dp[i]);
    }
}