AtCoder - Petrozavodsk - Contest - 001 - D (缩点 + 贪心 + 错误总结)
D - Forest
Time limit : 2sec / Memory limit : 256MB
Score : 600 points
Problem Statement
You are given a forest with N vertices and M edges. The vertices are numbered 0 through N−1. The edges are given in the format (xi,yi), which means that Vertex xi and yi are connected by an edge.
Each vertex i has a value ai. You want to add edges in the given forest so that the forest becomes connected. To add an edge, you choose two different vertices i and j, then span an edge between i and j. This operation costs ai+aj dollars, and afterward neither Vertex i nor j can be selected again.
Find the minimum total cost required to make the forest connected, or print Impossible if it is impossible.
Constraints
1≤N≤100,000
0≤M≤N−1
1≤ai≤109
0≤xi,yi≤N−1
The given graph is a forest.
All input values are integers.
Input
Input is given from Standard Input in the following format:
N M
a0 a1 .. aN−1
x1 y1
x2 y2
:
xM yM
Output
Print the minimum total cost required to make the forest connected, or print Impossible if it is impossible.
Sample Input 1
Copy
7 5
1 2 3 4 5 6 7
3 0
4 0
1 2
1 3
5 6
Sample Output 1
Copy
7
If we connect vertices 0 and 5, the graph becomes connected, for the cost of 1+6=7 dollars.
Sample Input 2
Copy
5 0
3 1 4 1 5
Sample Output 2
Copy
Impossible
We can’t make the graph connected.
Sample Input 3
Copy
1 0
5
Sample Output 3
Copy
0
The graph is already connected, so we do not need to add any edges.
Submit
题目链接: https://apc001.contest.atcoder.jp/tasks/apc001_d
题意:就是给你 n(编号 0 ~ n - 1) 个点,m 条边以及每个点的点权。
问:要使所有点形成一个联通块最少的花费?(点 i 和 点 j 相连 花费增加 cost[i] + cost[j],且每个点只能选一次)
一开始给的图是森林。
数据范围:

解题思路:
- 因为图一开始给的就是 森林,说明有 n - m 个部分,每一部分都是 一棵树。
- 若 m = n - 1 ,则说明这幅图一开始就是一棵树,输出 0。
- 若不考虑每个点最多被选一次,则需要再连 n - m - 1 条 边。
- 若考虑每个点最多被选一次,则至少需要 2 * (n - m - 1) 个 点(每一条边两端分别有一个点),否则输出 Impossible。
- 若 n >= 2 * ( n - m - 1) 时,先在每一部分( 缩点 )选当前部分点权 最小( 优先队列 )的点加到答案里,剩下的点依次选 最小 的点权,直到选够 2 * (n - m - 1) 个点为止。
- 复杂度:O(nlgn)
错误总结:我一开始写采用的方法是:依次把每个部分合并,一边合并一边用优先队列维护每部分的最小点权值。但这样写是错的,比如以下样例:
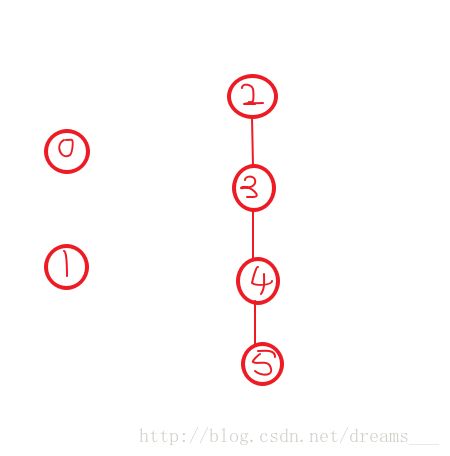
若按照我原先的方法来选的话(先忽略点权),先是选 0号点 和 1号点 合并,之后 0号点 和 1号点 都不能再次被选了,就会输出 Impossible。但其实只要 0号点 与 2号点 连,1 号点 与 3号点 连就可以了。
解题代码:
#includevector, greater > que;
int n,m,ind,cnt;
void dfs(int x){//缩点
low[x] = dfn[x] = ++ind;
st.push(x),vis[x] = 1;
for(int i = 0;i < G[x].size();i++){
int v = G[x][i];
if(!dfn[v]){
dfs(v);
low[x] = min(low[x],low[v]);
}
else if(vis[v]){
low[x] = min(low[x],dfn[v]);
}
}
if(low[x] == dfn[x]){
int all = 0;
cnt++;
bool flag = false;
while(!st.empty()){
int tot = st.top();
st.pop();
vis[tot] = 0;
in[tot] = 0;
in[tot] = cnt;
p[++all] = cost[tot];
flag = true;
if(tot == x) break;
}
if(flag){
sort(p + 1,p + 1 + all);
sum += p[1];
num++;
for(int i = 2;i <= all;i++) que.push(p[i]);
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 0;i < n;i++) scanf("%lld",&cost[i]);
for(int i = 1;i <= m;i++){
int x,y;
scanf("%d %d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
if(n < 2 * (n - m - 1)){
printf("Impossible\n");
return 0;
}
else if(n == m + 1){
printf("0\n");
return 0;
}
for(int i = 0;i < n;i++){
if(!dfn[i]) dfs(i);
}
while(num < 2 * (n - m - 1)){
if(!que.empty()){
LL ans = que.top();
que.pop();
sum += ans;
num++;
}
}
printf("%lld\n",sum);
return 0;
}