Codeforces Round #627 (Div. 3) F. Maximum White Subtree(树dp)

Codeforces Round #627 (Div. 3) F. Maximum White Subtree(树dp)

F. Maximum White Subtree
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a tree consisting of n vertices. A tree is a connected undirected graph with n−1 edges. Each vertex v of this tree has a color assigned to it (av=1 if the vertex v is white and 0 if the vertex v is black).

You have to solve the following problem for each vertex v: what is the maximum difference between the number of white and the number of black vertices you can obtain if you choose some subtree of the given tree that contains the vertex v? The subtree of the tree is the connected subgraph of the given tree. More formally, if you choose the subtree that contains cntw white vertices and cntb black vertices, you have to maximize cntw−cntb.

Input
The first line of the input contains one integer n (2≤n≤2⋅105) — the number of vertices in the tree.

The second line of the input contains n integers a1,a2,…,an (0≤ai≤1), where ai is the color of the i-th vertex.

Each of the next n−1 lines describes an edge of the tree. Edge i is denoted by two integers ui and vi, the labels of vertices it connects (1≤ui,vi≤n,ui≠vi).

It is guaranteed that the given edges form a tree.

Output
Print n integers res1,res2,…,resn, where resi is the maximum possible difference between the number of white and black vertices in some subtree that contains the vertex i.

Examples
inputCopy
9
0 1 1 1 0 0 0 0 1
1 2
1 3
3 4
3 5
2 6
4 7
6 8
5 9
outputCopy
2 2 2 2 2 1 1 0 2
inputCopy
4
0 0 1 0
1 2
1 3
1 4
outputCopy
0 -1 1 -1
Note
The first example is shown below:

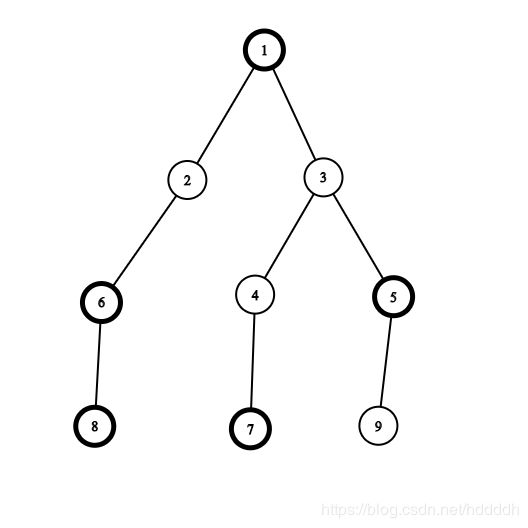
The black vertices have bold borders.

In the second example, the best subtree for vertices 2,3 and 4 are vertices 2,3 and 4 correspondingly. And the best subtree for the vertex 1 is the subtree consisting of vertices 1 and 3.

题意 :给n个点 n-1条边 点分成黑色和白色点 （保证生成一棵树） 求每个点联通子图内 白点个数减黑点个数最大。
例如 样例1 对于1 这个点选 1 2 3 4 答案为 2.

ps :因为前几天刚 做过 学长出的两道 毒瘤的树dp 所以想把这题补一下 发现这题和那两题差不多；

思路 ：
1.
我们可以先求 每个点对于其子树内的点可以取得的最大权值 记为 dp[i] 一开始将黑点赋值 -1 白点赋值 1
可以得到 dp[i]+=max(0,dp[j]) (j为i的子节点)。(解释一下 如果其子节点值小于0 就不用加)。
实现这个步骤 dfs 即可 自下而上求。
2.
处理完第一步之后 我们可以发现 对于 根节点 我们的答案就是其 dp 因为其不含子树外的点。
3.
这时候我们就要考虑 对于其他的点 其子树外 产生的贡献是多少。我们计答案为 ans[j] (i表示其父节点)
可以得到转移方程：
ans[j]=dp[j]+max (0 , ans [i] - max ( 0 , dp [j] ) ) .
ans [i] - max ( 0 , dp [j] ) 代表上一个节点的答案 减去这个节点产生的贡献 就为该节点子树外的贡献

代码

#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=2e5+7;
int head[maxn],a[maxn],dp[maxn],ans[maxn],num=0;
struct node{
      int to,next;
}e[maxn<<1];
void add(int u,int v){
    e[num].next=head[u];
    e[num].to=v;
    head[u]=num++;
}
void dfs1(int u,int fa){
     if(a[u]) dp[u]=1;
     else dp[u]=-1;
     for(int i=head[u];i!=-1;i=e[i].next){
        int v=e[i].to;
        if(v==fa) continue;
        dfs1(v,u);
        dp[u]+=max(0,dp[v]);
     }
}
void dfs2(int u,int fa){
    if(u==1) ans[u]=dp[u];
    for(int i=head[u];i!=-1;i=e[i].next){
        int v=e[i].to;
        if(v==fa) continue;
        ans[v]=dp[v]+max(0,ans[u]-max(0,dp[v]));
        dfs2(v,u);
    }
}

int main (){
   int k,u,v;
   cin>>k;
   memset(head,-1,sizeof(head));
   for(int i=1;i<=k;i++){
       scanf("%d",&a[i]);
   }
   for(int i=0;i<k-1;i++){
      scanf("%d%d",&u,&v);
      add(u,v);
      add(v,u);
   }
   dfs1(1,-1);
   dfs2(1,-1);
   for(int i=1;i<=k;i++) printf ("%d ",ans[i]);
   }
 
 

ps :第一次写 这种2000分的题 比较水 多多包涵